Regresión

En este documento vamos a hablar de la regresión, una importante herramienta de predicción que nos va a ayudar a inferir ciertos valores de salida en base a un conjunto de datos de entrada, siempre que podamos establecer una conexión o relación entre los datos de entrada y el resultado esperado. Veremos primero los fundamentos básicos sobre los que se asienta la regresión, para luego ver algunos tipos de regresión distintos que podemos aplicar.

1. Fundamentos de la regresión

La regresión, como hemos dicho, consiste en definir un sistema de predicción o estimación de valores de una variable dependiente respecto a una o varias variables independientes. Imaginemos que tenemos las alturas en centímetros de varias personas, y la talla de zapato que utilizan:

Altura	Talla
185	44
170	39
178	42
160	36
190	46
180	43
195	47
158	35
163	36
171	42
181	43
168	38
175	40
166	37
191	46

Podemos emplear alguna librería como Matplotlib para dibujar un gráfico de dispersión de estos datos:

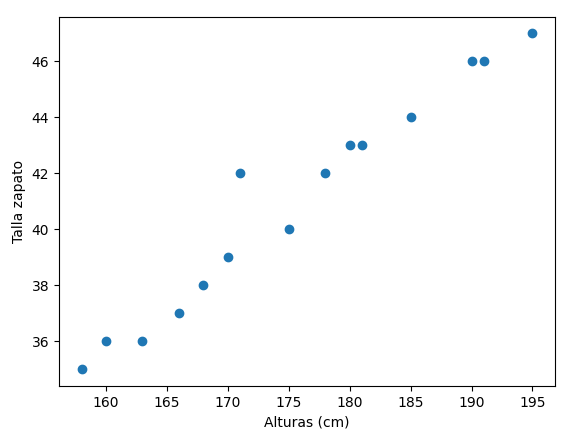
Como podemos ver, existe cierta dependencia entre estos dos datos (a medida que aumenta la altura, la talla aumenta en igual proporción), y podríamos estimar, dada la altura de una persona, qué talla de zapatos es probable que utilice. Básicamente, en este caso, consiste en detectar cuál es la recta que mejor se ajusta a los puntos que hemos dibujado en el gráfico anterior. Para cualquier x que no hayamos contemplado, la y estimada será la coordenada de esa recta en esa x.

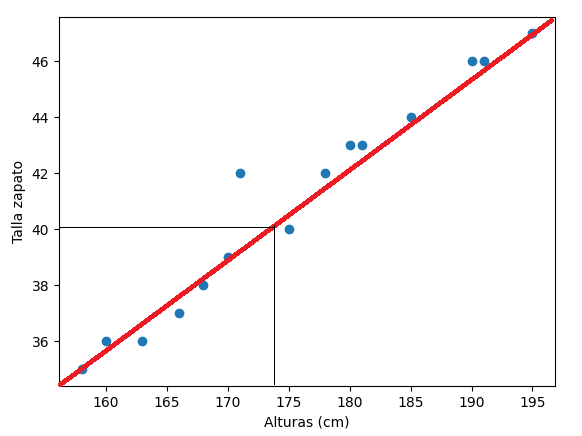
1.1. Tipos de regresión

En general, podemos hablar de cuatro tipos distintos de regresión:

• Regresión lineal, donde existe una dependencia lineal entre la(s) variable(s) independiente(s) y la variable dependiente. A su vez, puede ser:
  • Simple: sólo hay una variable independiente
  • Múltiple: existen varias variables independientes relacionadas con la variable dependiente
• Regresión logística: no existe una dependencia lineal entre las variables independientes y la dependiente, sino que la relación es algo más compleja. A su vez, también pueden ser simples o múltiples, dependiendo de cuántas variables independientes entren en juego.

2. Regresión lineal

Trataremos en este apartado los distintos modos de regresión lineal que existen: simple y múltiple.

2.1. Regresión lineal simple

La regresión lineal simple es aquella en la que hay una dependencia lineal entre dos variables, una independiente x y otra dependiente y, de forma que podemos estimar y aplicando un coeficiente a sobre x y sumándole en todo caso un desvío b:

y = ax + b

En el ejemplo anterior:

• La variable independiente x es la altura de las personas, y la variable dependiente y es la talla de zapato que queremos estimar.
• El coeficiente a por el que multiplicamos a la x determina la pendiente o inclinación de la recta de ajuste, o en otras palabras, cuánto debería incrementarse la talla del zapato a medida que incrementamos la altura de la persona.
• El término b que sumamos al final lo que hace es desplazar verticalmente la recta más arriba o más abajo en el eje Y, para ajustarla mejor a los puntos. Indica también cuánto debería valer la variable dependiente y cuando la independiente es 0.

2.1.1. Ajuste de la recta. Método de los mínimos cuadrados

¿Cómo se calcula la recta que mejor se ajusta a los puntos de un sistema de regresión lineal simple? Debemos obtener aquella recta para la que los puntos "reales" de nuestra colección de datos se separen lo mínimo posible de ella, en conjunto. Para cada pareja x e y de mi tabla de datos, tendré que ver cuál es el valor que predeciría la recta (llamémosle y2, por ejemplo), y calcular la diferencia entre el valor real y y el valor que predice la recta y2, y repetir este proceso para todos los puntos de mi tabla. Al final, me quedaré con la recta que tenga una suma de distancias mínima. Como la diferencia y - y2 puede ser positiva o negativa, lo que se hace es elevar al cuadrado la resta. Así, buscaremos una recta que minimice la suma de diferencias al cuadrado:

min(sum(y - y2))

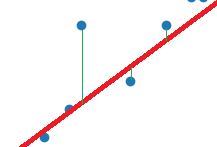
Esta expresión se llama método de los mínimos cuadrados, y es la estrategia que se utiliza, por tanto, para ajustar la recta en una regresión lineal. Afortunadamente para nosotros, no tenemos que preocuparnos de este cálculo, ya que hay librerías que lo hacen por nosotros.

2.1.2. Regresión lineal simple en Python

Veamos cómo podríamos aplicar la regresión lineal simple en Python usando un ejemplo como el anterior. Supondremos que ya tenemos cargado un data frame de Pandas con dos columnas (Altura y Talla), en la variable datos. Comenzaremos por definir el conjunto X con la(s) variable(s) independiente(s) (la altura en este caso) y el vector y con la dependiente (talla). También dividiremos estos conjuntos en entrenamiento y test, algo muy habitual en todo proceso de machine learning

import pandas as pd
from sklearn.model_selection import train_test_split

# ... Aquí suponemos que cargamos el data frame "datos"

X = datos['Altura'].values.reshape(-1, 1)
y = datos['Talla'].values.reshape(-1, 1)

X_train, X_test, y_train, y_test = \
    train_test_split(X, y, test_size = 0.2, random_state = 0)

Nota

Hacemos una operación de reshape(-1, 1) sobre los datos X e Y para crear un tamaño de filas indeterminado, y 1 columna. Esto es así porque la regresión lineal simple necesitará dos columnas de datos, una para las X y otra para las Y.

A continuación, usaremos la clase LinearRegression de SciKit Learn para que haga el trabajo sucio por nosotros:

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

...

regression = LinearRegression()
regression.fit(X_train, y_train)

Como podemos ver, basta con inicializar el objeto y pasarle al método fit el conjunto de variables independientes (X_train en nuestro caso) y las variables dependientes asociadas reales (y_train). Es importante que ambos datos tengan la misma longitud (mismo número de filas).

El siguiente paso será comprobar el modelo de regresión creado con nuevos datos de entrada (los de test). Invocaremos para ello al método predict de nuestro modelo de regresión ya entrenado, y le pasaremos como parámetro los datos X de test. Lo que obtendremos serán predicciones sobre esos datos, que podemos guardar en una variable y_pred, por ejemplo:

y_pred = regression.predict(X_test)

Como también tenemos los resultados reales de esos datos de test, podemos comprobar cómo de alejados o cercanos han sido los datos predichos, comparando los datos de ambos vectores y_pred e y_test. También podemos obtener una representación visual de todo este proceso de regresión usando Matplotlib.

import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

...

# Puntos reales
plt.scatter(X_train, y_train, color="blue")
# Recta de regresión (predecimos las Y sobre las X de entrenamiento)
plt.plot(X_train, regression.predict(X_train), color="red")
plt.xlabel("Altura (cm)")
plt.ylabel("Talla de zapato")
plt.show()

Evidentemente, cuantos más datos tengamos en el conjunto de entrenamiento, más precisa será la recta, aunque podemos caer en el caso de overfitting: que se ajuste demasiado a ese conjunto pero no prediga correctamente los del conjunto de test. También tenemos que asegurarnos de que existe una relación lineal entre las dos variables, es decir, que la recta no se va alejando cada vez más de los puntos a medida que avanzamos en el eje X.

Aquí puedes descargar el ejemplo completo de los pasos seguidos en este apartado.

2.2. Regresión lineal múltiple

En la regresión lineal múltiple no entra una sola variable independiente en juego (como la altura de las personas en el ejemplo anterior) sino varias. Por ejemplo, podríamos estimar la nota final de un examen por parte de un alumno en base a varios factores: cuántas horas de estudio ha dedicado semanalmente a la asignatura, cuántas faltas de asistencia ha tenido, cuántas horas de sueño tiene al día... También pueden entrar en juego variables categóricas (ordinales o no), como por ejemplo el medio en que viene a clase (a pie, autobús, coche...). Esto puede crear una tabla como la siguiente:

Horas_Estudio	Faltas	Horas_Sueño	Desplazamiento	Nota
6	2	7	Pie	8
2	10	5	Bus	4
5	2	7	Coche	7
8	1	6	Pie	8
3	3	5	Coche	3
7	3	6	Bus	7
4	0	6	Coche	6
5	5	8	Pie	6
8	4	8	Pie	9
6	2	7	Bus	6

2.2.1. Selección de las características relevantes

Lo primero que tenemos que tener en cuenta es que, una vez tenemos la tabla con los datos de entrada, hemos de averiguar si todos los datos van a ser relevantes para calcular el resultado (la nota, en este caso) o habrá columnas que no aporten nada en la estimación y podamos prescindir de ellas. Es importante simplificar nuestro modelo al máximo para que sea más fácil de programar, y también más fácil de entender.

Existen varias estrategias para seleccionar los atributos más relevantes para nuestro estudio:

• Método exhaustivo u all-in: consiste en tomar de entrada todas las variables posibles. Esto suele hacerse cuando, por experiencia previa, sabemos que todas van a ser importantes, o también como paso previo a la estrategia de eliminación hacia atrás.
• Eliminación hacia atrás: a partir de todas las variables, se define lo que se llama un nivel de significación o SL, que típicamente se suele fijar en 0.05. Después, de forma repetitiva, se va calculando el modelo con las variables incluidas, se ve si alguna tiene un valor (conocido como p-valor) que exceda ese nivel de significación, y se van eliminando del conjunto, repitiendo el proceso hasta que ninguna variable supere ese nivel.
• Selección hacia adelante: tiene un funcionamiento inverso al anterior. Se define también un nivel de significación SL, pero lo usaremos para entrar en el modelo en lugar de para salir de él. Definimos un modelo lineal simple para cada variable x y nos quedamos con el que tenga menor p-valor. Después, ajustamos el resto de modelos añadiendo esa nueva variable (tendremos modelos de 2 variables). Repetimos este proceso añadiendo cada vez una nueva variable, hasta que excedamos el SL establecido. En este caso, recuperaremos el modelo anterior a ese paso.
• Eliminación bidireccional, que de algún modo combina los dos anteriores. Definimos un SL para entrar y otro para salir del modelo. Iniciamos entonces un paso de selección hacia adelante con las variables que no lleguen al SL de entrada, y le seguirán pasos de eliminación hacia atrás para descartar variables que excedan el SL de salida. Por ejemplo, si en un momento determinado pasamos de 4 a 5 variables, nos aseguramos de que ninguna de esas 5 variables supera el SL de salida, de lo contrario la quitamos e intentamos añadir otra. El proceso terminará cuando ya no queden variables candidatas para entrar ni para salir. Es, quizá, la mejor estrategia posible (aunque la más costosa de aplicar).
• Comparación de resultados: se generan todos los modelos posibles (1 variable, 2 variables, 3 variables) y se elige el que mejor resultado ofrece. Es un método de fuerza bruta que genera todas las posibles opciones. Para N columnas se generan (2^N) - 1 modelos distintos.

2.3. Requisitos para poder aplicar regresión lineal

Si queremos aplicar regresión lineal sobre los datos de un problema, se deben cumplir una serie de requisitos previos.

• Ausencia de multicolinealidad: en nuestro conjunto de variables independientes X no puede haber ninguna que dependa de otra. En nuestro ejemplo anterior, una vez hemos transformado la columna Desplazamiento en variables dummy o codificación one hot, no podemos incluir todas las columnas one hot en el estudio, porque entonces habrá una colinealidad entre ellas. Siempre debemos dejar, en este caso, una de las columnas sin incluir para evitar esa colinealidad, o de lo contrario el sistema no podrá aprender a evaluar el impacto que puedan tener estos factores por separado.