Redes multicapa y ajuste de hiperparámetros¶
En este documento profundizaremos más en el desarrollo de redes profundas, entendiendo este concepto como redes con varias capas (ocultas). El hecho de añadir capas ocultas, como veremos, permitirá definir más especificidad y jerarquización en la toma de decisiones. También aprovecharemos este documento para profundizar más en algunas cosas que dejamos en el tintero en documentos anteriores, como el ajuste de parámetros relevantes en las redes, y la visualización gráfica del proceso de aprendizaje.
1. Caracteristicas de los MLPs¶
La idea de perceptrón multicapa (MLP, Multi-Layer Perceptron) fue concebida por Rumelhart, Hinton y Williams en 1986. En aquel entonces la capacidad computacional de los ordenadores era muy reducida, por lo que las posibilidades prácticas de construir redes complejas que entrenaran y resolvieran problemas en un tiempo razonable era muy limitada. Varias décadas después, con el avance de los dispositivos hardware (GPUs, TPUs, procesamiento paralelo, capacidad de almacenamiento...) sí estamos en disposición de desarrollar este tipo de redes con garantías.
Como su nombre indica, un perceptrón multicapa es una red neuronal compuesta de varias capas. En ejemplos anteriores hemos llegado a construir redes con una capa de entrada, una capa oculta y una de salida. Esto ya puede considerarse un MLP, pero en realidad podemos extender las capas ocultas todo lo que queramos y necesitemos. Veremos a continuación qué implica tener más capas ocultas, cómo determinar la cantidad de capas ocultas necesarias y qué otros factores podemos y debemos tener en cuenta al aumentar la complejidad de nuestras redes.
1.1. ¿Qué son los tensores?¶
En algunos apartados de apuntes previos se ha mencionado el concepto de tensor, sin hacer demasiado hincapié en qué significa exactamente. De hecho, la propia librería que usamos se llama TensorFlow, y algunos componentes software como las TPU (Tensor Processing Unit) hacen referencia a este concepto. Así que conviene saber a qué nos estamos refiriendo exactamente.
Un tensor es un elemento matemático que almacena un conjunto de valores numéricos. Puede ser unidimensional (vector), bidimensional (matriz) o de más dimensiones. Estos tensores en Python se almacenan en forma de arrays NumPy, normalmente.
Así, por ejemplo, si queremos analizar un conjunto de tuits de 1.000 usuarios, cada uno con hasta 280 caracteres, podemos usar un tensor 2D de tamaño (1000, 280). Si queremos procesar una imagen RGB de 640 x 480 píxeles, necesitaremos un tensor 3D (640, 480, 3), siendo 3 el número de colores diferentes en cada píxel. Para una secuencia de 1.000 imágenes de este tipo necesitaremos un tensor 4D (1.000, 640, 480, 3).
Así, la idea tras TensorFlow es hacer pasar estos tensores por la red y hacer cálculos matemáticos con los datos que almacenan, para obtener un resultado (multiplicando los valores de entrada con los pesos de las conexiones de cada capa). Y la funcionalidad principal de las TPUs es aumentar la eficiencia en el procesamiento matemático de este conjunto de datos, aplicado fundamentalmente al terreno del machine/deep learning.
2. Definiendo un MLP. Opciones relevantes¶
Vamos a definir un perceptrón multicapa para el siguiente problema: disponemos de este archivo CSV sobre datos de distintos pacientes (aquí podemos consultar el original en Kaggle). En base a distintos parámetros (número de embarazos, nivel de glucosa en sangre, presión sanguínea, etc) se intenta predecir si esa persona tiene o no diabetes (última columna Outcome). Vamos a definir una red neuronal multicapa para calcular esa predicción.
Comenzamos leyendo los datos y procesándolos: en este caso los valores de X corresponden a todas las columnas menos la última, y la columna y es esa última columna de Outcome. Además, escalamos los valores de entrada usando el StandardScaler de SKLearn que ya hemos utilizado en otros ejemplos previos:
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from keras.models import Sequential
from keras.layers import Input, Dense
# Preparación de datos
datos = pd.read_csv('diabetes.csv')
scaler_X = StandardScaler()
X = datos.iloc[:, :-1]
X = scaler_X.fit_transform(X)
y = datos.iloc[:, -1]
En este caso, construiremos la red de una forma diferente, aunque equivalente a documentos anteriores. Usaremos el constructor de la clase Sequential para pasarle como parámetro la lista de capas que queremos añadir. Construiremos un MLP con dos capas ocultas de muchas neuronas, y una capa de salida de 1 neurona con la predicción (activación sigmoidea):
modelo = Sequential([
Input(shape=(X.shape[1],)),
Dense(800, activation='relu'),
Dense(300, activation='relu'),
Dense(1, activation='sigmoid')
])
Si echamos un vistazo al resumen del modelo con su método summary, obtendremos algo así:
________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
dense (Dense) (None, 800) 7200
dense_1 (Dense) (None, 300) 240300
dense_2 (Dense) (None, 1) 301
=================================================================
Total params: 247,801
Trainable params: 247,801
Non-trainable params: 0
_________________________________________________________________
Nos podemos hacer una idea de la cantidad de parámetros (pesos y biases) que se pueden configurar en una red de este tamaño.
Finalmente, vamos a compilar y entrenar nuestra red. Usaremos como función de pérdida la entropía cruzada binaria, como hemos hecho en otros problemas previos de clasificación binaria, y optimizador sgd.
modelo.compile(loss='binary_crossentropy', optimizer='sgd', metrics=['accuracy'])
datos_entrenamiento = modelo.fit(X, y, validation_split=0.2, epochs=200)
En base a los resultados que obtendremos, vamos a analizar a continuación algunos aspectos relevantes y proponer mejoras.
2.1. Reproducibilidad de los resultados¶
Cuando estamos desarrollando un modelo estocástico como es una red neuronal puede resultar interesante poder reproducir siempre los mismos resultados, para ver cómo afectan las mejoras que añadimos a dicho modelo. Esto puede conseguirse estableciendo de entrada una semilla fija (seed) para generar los números aleatorios. Lo haremos utilizando la función set_random_seed de keras.utils:
from keras.utils import set_random_seed
...
# Esto debe ir al principio del código
set_random_seed(0)
El número que pongamos como semilla es irrelevante, puede ser cualquiera. Adicionalmente (dependiendo de la versión de Keras/TensorFlow que estemos utilizando) puede ser necesario compaginar esta instrucción con la instrucción seed de NumPy, que se utiliza internamente para generar vectores con datos aleatorios:
from numpy.random import seed
from keras.utils import set_random_seed
...
seed(0)
set_random_seed(0)
Nuevamente, los números elegidos como semilla pueden ser otros, y también distintos entre sí. En principio, únicamente con set_random_seed nos puede ser suficiente para reproducir resultados en versiones recientes de la librería, pero conviene tener presente esta última alternativa por si nos es necesaria.
2.2. Gráficas de seguimiento¶
Una de las opciones que hemos comentado de pasada en documentos anteriores, y que hasta ahora no hemos utilizado, es la posibilidad de usar los datos que genera la función de entrenamiento fit. En concreto, proporciona una secuencia de valores de los parámetros de entrenamiento que hemos definido, tales como la pérdida loss o la exactitud accuracy. De este modo, podemos mostrar en un gráfico la evolución de estos datos.
Además, en el caso anterior, hemos empleado la propia función fit pasándole todo el conjunto X de datos, y la propia función se ha encargado de separar en entrenamiento y test, usando el parámetro validation_split para determinar el porcentaje que va a cada parte (20% para validación, en el ejemplo anterior). Esto es particularmente útil para gestionar estos gráficos, ya que en los datos del entrenamiento tendremos la evolución del coste y la exactitud tanto para el entrenamiento como para el test.
datos_entrenamiento = modelo.fit(X, y, validation_split=0.2, epochs=200)
Así, al finalizar el proceso de entrenamiento podemos mostrar una gráfica combinada de cómo ha evolucionado la función de pérdida en ambos conjuntos (entrenamiento y test), y también podemos hacer lo mismo con la exactitud. De hecho, podemos mostrar todos los parámetros (keys) que se almacenan en los datos_entrenamiento, para saber cuáles podemos visualizar:
print(datos_entrenamiento.history.keys())
# Gráfica combinada de pérdida en entrenamiento y test (val)
plt.plot(datos_entrenamiento.history['loss'])
plt.plot(datos_entrenamiento.history['val_loss'])
plt.title('Evolución del coste')
plt.ylabel('Coste')
plt.xlabel('Epoch')
plt.legend(['Entrenamiento', 'Test'], loc = 'upper left')
plt.show()
2.3. El overfitting¶
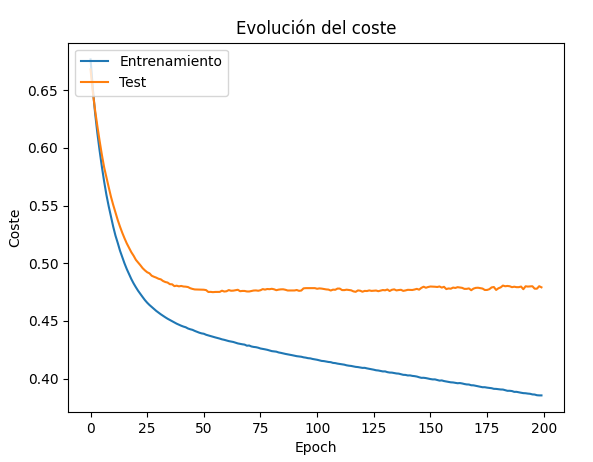
El overfitting es un fenómeno que puede darse en cualquier sistema de machine learning, aunque es más habitual en redes profundas, y consiste en un sobre-entrenamiento, en el cual la red se ha dedicado a memorizar el conjunto de datos de entrenamiento, pero no es capaz de inferir nuevos valores fuera de ese conjunto adecuadamente.
Es lo que ocurre con la red del ejemplo anterior. Como puede verse en la gráfica del coste o loss, hay un punto donde el coste en el conjunto de test deja de converger y decrecer, y se dispara. En ese punto es donde la red ha dejado de aprender cosas nuevas, y se ha centrado en memorizar el conjunto de entrenamiento.
¿Qué alternativas hay para solucionar este problema? Existen varias, vamos a mencionar algunas de ellas, teniendo en cuenta que no tenemos por qué limitarnos a una, y podemos escoger una combinación de varias.
Simplificar el modelo de entrada
Reducir el número de neuronas en las capas ocultas puede favorecer que la red no tenga nodos suficientes para memorizar todas las posibles combinaciones de valores de entrada y se "vea obligada" a generalizar resultados. En el ejemplo anterior, si limitamos el tamaño de las capas ocultas a 8 neuronas, por ejemplo, obtendremos unos resultados mejores para el conjunto de validación:
modelo = Sequential([
Input(shape=(X.shape[1],)),
Dense(8, activation='relu'),
Dense(8, activation='relu'),
Dense(1, activation='sigmoid')
])
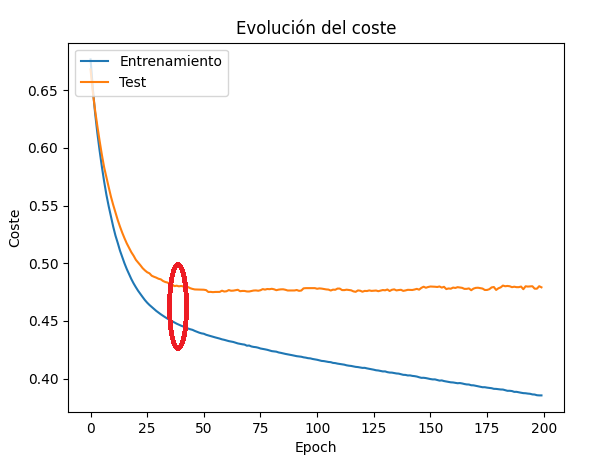
Early stopping
La técnica del early stopping consiste en detener el entrenamiento en cuanto se detecte el overfitting. En la gráfica anterior podemos ver que eso ocurre en torno a la epoch 40-50. Vamos a volver al modelo original de la red, con muchas neuronas, y usaremos la clase EarlyStopping de Keras para definir cuándo queremos parar:
from keras.callbacks import EarlyStopping
...
early_stop = EarlyStopping(monitor='val_loss', patience=5, \
restore_best_weights = True)
datos_entrenamiento = modelo.fit(X, y, validation_split=0.2, epochs=200, \
callbacks=[early_stop])
En los parámetros del constructor indicamos:
- Qué variable queremos monitorizar, en el parámetro
monitor. En este caso queremos monitorizar el coste en el conjunto de validación (val_loss) - El parámetro
patienceindica cuántas iteraciones vamos a admitir sin que el valor decrezca. En nuestro caso, si después de 5 iteraciones el valor sigue subiendo, detendremos el entrenamiento - El parámetro
restore_best_weightsindica que, al detener el entrenamiento, recuperaremos los pesos de la mejor solución obtenida hasta ese momento (hace 5 iteraciones, en nuestro caso). - Finalmente, observa que usamos este elemento (variable
early_stop) como callback de la función de entrenamiento (parámetrocallbacksde la funciónfit).
Al ejecutar el modelo original con esta nueva opción, vemos que el resultado se detiene en la iteración 52 aproximadamente, después de 5 iteraciones sin que la curva de test decrezca:
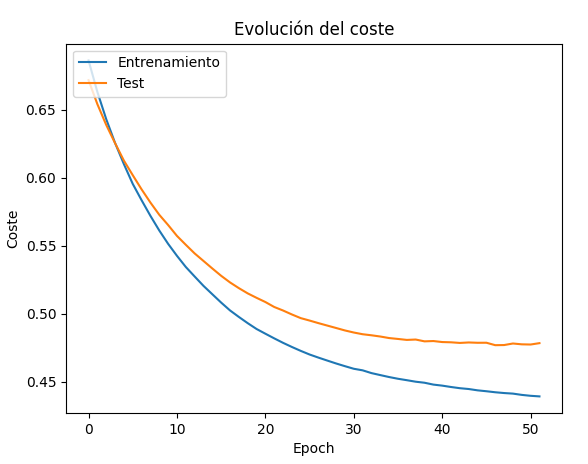
Capas dropout
Las técnica de dropout permite separar o desconectar neuronas arbitrariamente en cada etapa del entrenamiento, evitando así que se memoricen pesos y rutas predeterminadas para unos datos de entrada concretos. Lo analizaremos con más detalle a continuación
2.4. Las capas de Dropout¶
La técnica de Dropout fue propuesta por primera vez en 2012 por G. Hinton, uno de los padres del perceptrón multicapa. Esta técnica permite desconectar aleatoriamente neuronas de una capa en cada etapa del entrenamiento, evitando así que los pesos se acomoden a memorizar un conjunto fijado de datos.
TensorFlow y Keras permiten utilizar un tipo especial de capa llamada Dropout, dentro del paquete keras.layers. Esta capa permite especificar un porcentaje de desconexiones con respecto a la capa previa. ¿Qué significa esto exactamente? Como ya sabemos, cada vez que añadimos una capa Dense en una red neuronal, ésta conecta automáticamente todas sus neuronas con todas las neuronas de la capa anterior. Si añadimos en medio una capa Dropout con una tasa de desconexión de 0.2, por ejemplo, esto significa que el 20% de las neuronas de la capa previa se van a desconectar en cada epoch, de forma aleatoria. Esto facilitará que la red no se "acostumbre" a usar unos pesos fijos para memorizar los datos de entrenamiento, y se vea obligada a buscar otras alternativas de combinación de pesos para obtener buenos resultados.
Aquí vemos un ejemplo sencillo, en el que añadimos una capa Dropout que desconecta el 20% de las neuronas de la capa de entrada en sus conexiones con la primera capa oculta:
from keras.models import Sequential
from keras.layers import Input, Dense, Dropout
modelo = Sequential()
Input(shape=(X.shape[1],)),
modelo.add(Dropout(0.2)),
model.add(Dense(60, activation='relu'))
Veamos qué utilidad tiene esto sobre el ejemplo anterior, donde había overtfitting. Aplicaremos una capa de dropout entre la primera y la segunda capa oculta, y otra entre la capa oculta y la de salida. En cada una haremos que se desconecten el 20% de las neuronas.
from keras.layers import Dense, Dropout, Input
...
modelo = Sequential([
Input(shape=(X.shape[1],)),
Dense(8, activation='relu'),
Dropout(0.2),
Dense(8, activation='relu'),
Dropout(0.2),
Dense(1, activation='sigmoid')
])
Con esto se mejoran los resultados de la función de coste para el conjunto de validación, ajustándose mejor a los esperados por el entrenamiento. A cambio, vemos que el coste en el entrenamiento da unos pequeños saltos en su evolución, fruto de las desconexiones que se sufren en cada etapa.
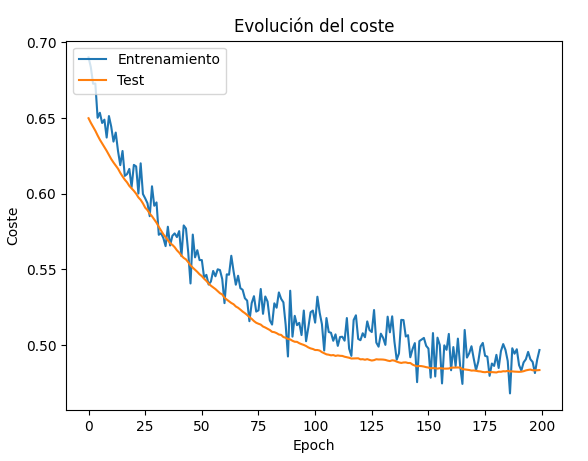
Hay que tener en cuenta que las desconexiones sólo se producen durante la etapa de entrenamiento, no en la validación y posterior inferencia.
Dónde y cómo aplicar dropout
¿Dónde se puede aplicar una capa de dropout? Existen varias teorías al respecto, y todo dependerá de la red en sí. A veces es conveniente aplicarla a la entrada, como en el ejemplo que hemos visto antes, y en otras ocasiones se aconseja dejarlo para los últimos niveles de capas ocultas.
La segunda pregunta que podemos hacernos es... ¿qué porcentaje de dropout es recomendable?. Normalmente suele ser un porcentaje bajo, entorno al 10%-30%. Hay que tener en cuenta que:
- Un porcentaje excesivamente alto puede provocar que la red no llegue a aprender, porque estaremos desconectando constantemente muchas neuronas en cada capa
- Un porcentaje demasiado bajo puede hacer que no se note el efecto, y no se reduzca significativamente el overfitting, al haber demasiadas conexiones permanentes.
Aquí puedes descargar el código fuente de las distintas versiones que hemos probado del ejemplo sobre la diabetes:
- v1: modelo simple con dos capas densas numerosas, para ver el overfitting en la gráfica
- v2: modelo con capas densas más simplificadas para reducir el overfitting
- v3: modelo basado en v1, donde se aplica early stopping cuando se detecta overfitting
- v4: modelo basado en v2 añadiendo capas Dropout para reducir el overfitting.
2.5. Ejemplo¶
Vamos a plantear un ejemplo diferente al que hemos visto anteriormente. Utilizaremos este dataset sobre datos de venta de coches. En el CSV existen diferentes columnas, que pasamos a explicar a continuación:
- price es el precio de venta del coche, catalogado en 4 categorías desde vhigh (muy alto) hasta low (bajo)
- maint es el precio de mantenimiento del coche, con las mismas 4 categorías anteriores
- doors es el número de puertas, categorizado en 2, 3, 4 o 5more (5 o más)
- capacity es la capacidad de personas que tiene el vehículo, categorizado como 2, 4 o más (more)
- luggage es el tamaño del maletero, categorizado como small, med o big
- safety es el nivel de seguridad del vehículo, categorizado como low, med o high
- result es nuestra columna objetivo, que indica el grado de aceptación del vehículo con los datos anteriores. Puede tomar los valores vgood (muy buena), good (buena), acc (aceptable) o unacc (inaceptable).
Como vemos, son todo datos categóricos, así que los vamos a reemplazar por códigos numéricos alternativos. En todos los casos nos interesa que haya un orden en esos valores, ya que, por ejemplo, un precio de mantenimiento high debe ser mayor que uno low. Aplicaremos, por tanto, las siguientes transformaciones:
datos = pd.read_csv('datos_coches.csv')
datos['price'] = datos['price'].map({'vhigh': 3, 'high': 2, 'med': 1, 'low': 0})
datos['maint'] = datos['maint'].map({'vhigh': 3, 'high': 2, 'med': 1, 'low': 0})
datos['doors'] = datos['doors'].map({'2': 2, '3': 3, '4': 4, '5more': 5})
datos['capacity'] = datos['capacity'].map({'2': 2, '4': 4, 'more': 5})
datos['luggage'] = datos['luggage'].map({'big': 2, 'med': 1, 'small': 0})
datos['safety'] = datos['safety'].map({'high': 2, 'med': 1, 'low': 0})
Vamos ahora a separar las columnas independientes X y la dependiente y. En esta última, aplicaremos una codificación one hot para categorizar en 4 columnas diferentes las 4 valoraciones distintas que se hacen:
X = datos.iloc[:, :-1]
y = datos.iloc[:, -1]
num_clases = len(y.unique())
y = pd.get_dummies(datos['result'], columns=['result'])
Ejercicio 1
A partir del pre-procesamiento de datos anterior, crea una red multicapa con las siguientes características:
- Capa de entrada de tantas neuronas como columnas relevantes haya
- Primera capa oculta de 30 neuronas, activación relu
- Segunda capa oculta de 30 neuronas, activación relu
- Capa de salida de tantas neuronas como posibles resultados haya, y activación softmax
Compila la red con función de pérdida categorical_crossentropy, optimizador adam y añadiendo la métrica de la exactitud (accuracy). Entrénala durante 100 epochs con una porcentaje de validación del 20%. Finalmente, muestra el gráfico de evolución de la función de coste para entrenamiento y test (loss y val_loss)
Ejercicio 2
Verás que el modelo anterior tiene overfitting. Aplica las medidas que consideres oportunas para lograr un mejor ajuste del coste y la exactitud en el conjunto de test. Por ejemplo, puedes añadir capas de Dropout con una tasa de 20% o 30%, o intentar re-ajustar el diseño de la red.
2.6. Guardando nuestro modelo¶
Ya hemos podido comprobar que entrenar un modelo, aunque las máquinas actuales sean más potentes que las de hace unas décadas, puede llevar un tiempo considerable. Si tenemos que pasar por el mismo proceso cada vez que queramos probar nuestra red con nuevos datos de entrada, estaremos perdiendo un tiempo precioso.
Afortunadamente, TensorFlow/Keras permite guardar un modelo entrenado para poderlo utilizar cuando necesitemos. Esto puede hacerse de formas diferentes:
- Guardando el modelo completo, a través del método
savedel modelo en cuestión. El formato de salida es un formato propio de Keras llamado HDF5 (extensión de archivo .h5), aunque también podemos especificar el formato .keras, más reciente. Luego podemos recuperar el modelo de nuevo conload_modeldel paquetekeras.models:
modelo.save('mi_modelo.h5');
# También sirve modelo.save('mi_modelo.keras')
...
otro_modelo = keras.models.load_model('mi_modelo.h5')
# Podemos directamente evaluar o hacer predicciones
y_pred = otro_modelo.predict(X_test)
- También podemos guardar los pesos de las conexiones. Esto puede resultar interesante si hemos encontrado una configuración que da resultados aceptables, pero queremos explorar otras posibilidades. De este modo, guardamos los pesos del modelo, y podemos recuperarlos y restablecerlos después. Usaremos el método
save_weightsdel modelo para guardar (en formato HDF5 o en el propio formato de TensorFlow, extensión .tf). Luego usamosload_weightspara cargarlos. En el caso de no quererlos guardar a archivo, porque sea algo temporal durante la ejecución, podemos usar los métodosget_weightsyset_weights:
modelo.save_weights('pesos_mi_modelo.h5')
...
modelo.load_weights('pesos_mi_modelo.h5')
# Alternativamente...
pesos = modelo.get_weights()
...
modelo.set_weights(pesos)
Ejercicio 3
Guarda el modelo que mejor hayas ajustado del ejercicio anterior en un archivo llamado estimacion_coches.h5. Cárgalo en un programa que le pedirá al usuario que introduzca los datos de entrada de un vehículo:
- Precio de venta: 3 (vhigh), 2 (high), 1 (med), 0 (low)
- Precio de mantenimiento (mismos valores que el caso anterior)
- Número de puertas: de 2 a 5
- Capacidad: 2, 4 o 5
- Tamaño del maletero: 2 (big), 1 (med), 0 (small)
- Seguridad del vehículo: 2 (high), 1 (med), 0 (low)
El programa debe emitir una salida con su veredicto, indicando cómo de probable es cada una de las 4 posibles categorías (vgood, good, acc, unacc).
2.6.1. Guardando parámetros de escalado¶
En el caso de que nuestro modelo haya utilizado un escalado, también es posible guardar en un fichero aparte los parámetros del escalado para aplicarlos después a nuevos datos de entrada. Por ejemplo, y como caso más habitual, supongamos que hemos utilizado el escalador StandardScaler de Scikit-Learn.
import pandas as pd
from sklearn.preprocessing import StandardScaler
...
datos = pd.read_csv('fichero.csv')
escalador = StandardScaler()
X = datos.iloc[:, :-1]
X = escalador.fit_transform(X)
En el momento en que hayamos "entrenado" al escalador con los datos de entrada con fit_transform, ya podemos guardar esos parámetros de escalado. Una forma sencilla de hacerlo es utilizando la librería joblib, que también se instala junto a Scikit-Learn. Dispone de un método dump para guardar datos a un fichero, y así podríamos nuestro escalador anterior:
import joblib
...
joblib.dump(escalador, 'datos_escalado.save')
A la hora de recuperar esos datos más adelante (o en otro fichero fuente) hacemos uso del método load de la misma librería joblib, y los guardamos en una variable (que será de tipo StandardScaler en este caso):
import joblib
...
escalador = joblib.load('datos_escalado.save')
...
X_escalado = escalador.transform(X_test)
2.7. Más sobre clasificadores¶
A estas alturas ya hemos desarrollado algunos modelos de clasificación, tanto binarios como categóricos. En el caso de clasificadores binarios basta con una neurona en la capa de salida con una activación sigmoide y entropía cruzada binaria (binary_crossentropy) para distinguir entre uno y otro caso. En cambio, en el caso del clasificador categórico hemos hecho una codificación one hot de la columna objetivo y hemos definido una neurona por cada categoría, con activación softmax y entropía cruzada categórica (categorical_crossentropy).
Sin embargo, en este último caso podemos optar por una alternativa diferente, que consiste en:
- Codificar la columna objetivo con label encoding (un valor numérico distinto para cada categoría)
- Definir tantas neuronas en la capa de salida como valores (categorías) haya
- Establecer como función de activación la entropía cruzada categórica dispera (
sparse_categorical_crossentropy)
Esta segunda alternativa ofrece algunas ventajas sobre la primera: es más adecuada si tenemos demasiadas clases (porque se generarían demasiadas columnas one hot, ocupando demasiada memoria).
Ejercicio 4
Adapta el ejemplo anterior de coches usando sparse_categorical_crossentropy y comprueba los resultados obtenidos. Puedes usar el mismo fichero de prueba de modelos del Ejercicio 3 y cargar uno u otro modelo para probar.
3. Otras métricas relevantes¶
Una vez llegados aquí, hemos desarrollado distintos modelos de redes de regresión y clasificación (tanto binaria como categórica). A la hora de evaluar cómo de bien o mal entrenado está el modelo, nos hemos centrado en las métricas del coste (loss) y, en el caso de modelos de clasificación, también en la exactitud (accuracy). Sin embargo, existen otras métricas que podemos calcular y que nos van a ayudar a determinar mejor lo bien o mal entrenado que está nuestro modelo.
Por ejemplo, a la hora de evaluar el comportamiento de un modelo de clasificación, aunque la exactitud es un valor importante, no podemos confiar sólo en él para valorar dicho comportamiento. Especialmente en modelos cuya respuesta es delicada, como predictores de salud (diabetes, tumores...) puede ser importante cotejar estas métricas con otras.
3.1. Clasificadores binarios¶
Retomemos el ejemplo de la diabetes que hemos hecho al inicio de este documento. En concreto, nos quedaremos con la versión v4 que paliaba el overfitting simplificando el modelo y añadiendo capas de Dropout. Vamos a añadir ahora algunos elementos estadísticos más como:
- Matriz de confusión: ayuda a visualizar la cantidad de casos correctamente detectados, y a valorar los falsos positivos y negativos
- Sensibilidad (recall): determina de todos los casos positivos reales que había, cuántos detecta correctamente el modelo
- Especificidad (specificity): determina de todos los casos negativos reales que había, cuántos detecta el modelo
- Precisión (precision): determina cuántos casos positivos había realmente entre los que identificó el modelo. Un valor bajo aquí indicaría que nuestro modelo da muchas "falsas alarmas" o detecta muchos casos positivos que no lo son.
- Puntuación F1 (F1 Score): es una mezcla equilibrada de sensibilidad y precisión. Un valor alto indica que el modelo es robusto detectando positivos.
- Curva ROC: la curva ROC (Receiver Operating Characteristic, Curva de Característica Operativa del Receptor) es un gráfico que muestra cómo se comporta el modelo a todos los niveles de umbral posibles. En un clasificador binario lo normal es usar un umbral de 0.5 para distinguir casos positivos (>= 0.5) y negativos (< 0.5), pero en ocasiones este umbral no es acertado, y la curva ROC juega con la especificidad y la sensibilidad vistas antes para determinar el comportamiento del modelo con varios umbrales.
- Área bajo la curva (AUC): relacionada con la curva ROC anterior, mide el área bidimensional que hay bajo la curva trazada, dando un valor entre 0 y 1. Un AUC de 1 da un modelo perfecto, y uno de 0.5 daría un modelo inútil, que acierta por azar. Valores inferiores a 0.5 indicarían que el modelo está prediciendo justo lo contrario de lo que debería.
Para añadir todos estos elementos podemos emplear el paquete sklearn.metrics. Con el método confusion_matrix sacamos la matriz de confusión, y con classification_report obtenemos el resto de estadísticas. Por otra parte, con roc_auc_score sacamos el área bajo la curva (AUC) y con roc_curve calculamos la curva ROC
from sklearn.metrics import confusion_matrix, classification_report, roc_auc_score, roc_curve
...
Matriz de confusión
Vamos a comenzar por obtener la matriz de confusión y saberla interpretar.
# Realizar predicciones (en este caso sobre todo X, pero podría ser X_test)
y_pred = modelo.predict(X)
# Como la salida de la sigmoide es una probabilidad (0 a 1),
# la convertimos a 0 o 1 usando un umbral de 0.5
y_pred_binary = (y_pred > 0.5).astype(int)
# Generar la matriz de confusión
cm = confusion_matrix(y, y_pred_binary)
print("Matriz de Confusión:")
print(cm)
Podemos también generar un mapa de calor con la matriz de confusión, usando Seaborn:
import matplotlib.pyplot as plt
import seaborn as sns
...
plt.figure(figsize=(6,4))
# El parámetro fmt indica el formato del texto que se muestra en cada celda,
#"d" para numérico
sns.heatmap(cm, annot=True, fmt="d", xticklabels=['No Diabetes', 'Diabetes'],
yticklabels=['No Diabetes', 'Diabetes'])
plt.xlabel('Predicción del Modelo')
plt.ylabel('Valor Real')
plt.title('Matriz de Confusión')
plt.show()
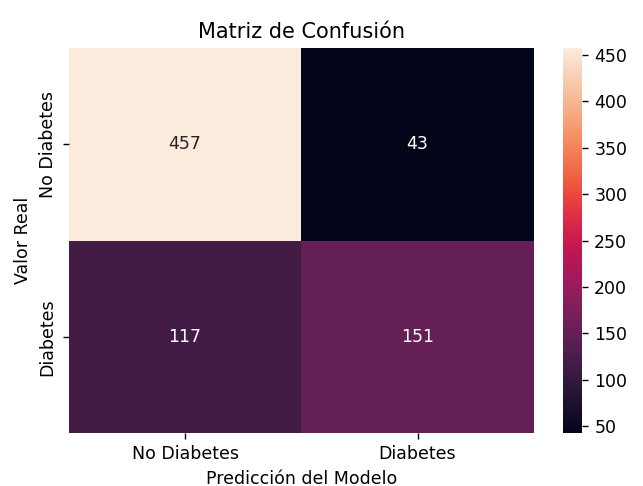
La matriz de confusión se interpreta de este modo:
| Predicho Negativo (0) | Predicho Positivo (1) | |
|---|---|---|
| Real Negativo (0) | Verdaderos Negativos (TN) | Falsos Positivos (FP) |
| Real Positivo (1) | Falsos Negativos (FN) | Verdaderos Positivos (TP) |
Informe de clasificación
Vamos a añadir ahora las métricas de sensibilidad (recall), especificidad (recall para casos negativos), precisión y exactitud (accuracy) y a conectarlas con la matriz de confusión para analizar los resultados.
# Informe de clasificación (Precisión, Recall, F1-score)
print("\nInforme de Clasificación:")
print(classification_report(y, y_pred_binary, target_names=['No Diabetes', 'Diabetes']))
Obtenemos esta tabla:
Informe de Clasificación:
precision recall f1-score support
No Diabetes 0.80 0.91 0.85 500
Diabetes 0.78 0.56 0.65 268
accuracy 0.79 768
macro avg 0.79 0.74 0.75 768
weighted avg 0.79 0.79 0.78 768
Observemos que la exactitud (accuracy) al finalizar el entrenamiento es del 79% según la tabla. Pero vamos a analizar el resto de métricas para determinar lo bueno o malo que es este resultado.
La especificidad se calcula los verdaderos negativos (TN) dividido entre el total de negativos (TN + FN) y la sensibilidad hace lo mismo con los positivos: TP / (TP + FP).
El análisis conjunto de estos datos podría ser el siguiente:
- Hay 500 pacientes negativos (sin diabetes), de los que hemos identificado correctamente 457, y se han escapado 43 que hemos etiquetado como diabéticos (falsos positivos). La especificidad (el recall para los casos negativos) es alta (0.91), lo que indica que se detectan muy bien los negativos.
- Hay 268 pacientes positivos (con diabetes), de los que hemos identificado correctamente 151, pero se han escapado 117 que hemos etiquetado como no diabéticos. La sensibilidad (el recall para los casos positivos) es baja (0.56), lo que indica que el modelo falla al detectar casi la mitad de los casos positivos.
- Respecto a la precisión (precision), indica, de todos los casos que el modelo clasificó como negativos (No diabetes) o como positivos (Diabetes), cuántos lo eran realmente. Se detectaron 457 negativos ciertos y 115 falsos, lo que da un 80% de precisión en negativos. Por otro lado, se detectaron 151 positivos ciertos y otros 43 que no lo eran, lo que da un 78% de precisión en positivos.
- El F1 Score es simplemente una media de la precisión y la sensibilidad. En el caso de los negativos, 0.91 y 0.8 dan un F1 Score medio de 0.85, lo que indica que el modelo es bueno detectando negativos. En el caso de los positivos, 0.56 y 0.78 dan un F1 Score medio de 0.65, lo que indica que el modelo falla en este aspecto, confirmando las métricas anteriores.
- Al final de la tabla tenemos una media ponderada (weighted avg), y una media macro (macro avg). La primera da más importancia a la clase más abundante (pacientes sanos, en este caso), y la segunda da la misma importancia a todas las clases. En este caso vemos que los valores son más o menos similares, en torno al 75-79%, pero sí es cierto que el macro avg es inferior porque los resultados en la clase menos predominante (pacientes con diabetes) son sensiblemente peores.
Curva ROC y área bajo la curva (AUC)
Vamos ahora a calcular la curva ROC y el área bajo la curva. En la curva ROC se representa, en el eje X, el opuesto a la especifidad (1 - especifidad) y en el eje Y la sensibilidad. El término (1 - especificidad) se conoce técnicamente como la Tasa de Falsos Positivos (FPR). En términos prácticos, es la respuesta a: "De todas las personas sanas, ¿a qué porcentaje voy a asustar dándoles un diagnóstico positivo por error?". Un valor pequeño indica que nuestro modelo acierta con las personas sanas o con los casos negativos, en general.
# Calcular el valor AUC sobre las probabilidades predichas (no el redondeo 0-1)
valor_auc = roc_auc_score(y, y_pred)
print(f"El AUC de mi modelo es: {valor_auc:.4f}")
# Dibujamos la curva ROC
fpr, tpr, _ = roc_curve(y, y_pred)
plt.plot(fpr, tpr, label=f'Modelo (AUC = {valor_auc:.2f})')
plt.plot([0, 1], [0, 1], 'k--') # Línea de azar
plt.xlabel('Falsos Positivos (1-Especificidad)')
plt.ylabel('Verdaderos Positivos (Sensibilidad)')
plt.legend()
plt.show()
Obtenemos una gráfica como esta:
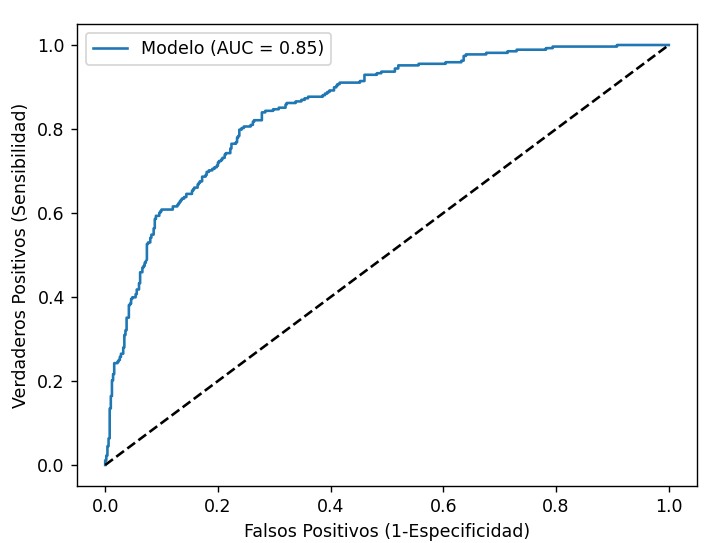
¿Cómo se interpreta esta curva?
- La recta punteada diagonal indica un AUC de 0.5. Si nuestra curva se acerca a esa recta es síntoma de que está acertando al azar.
- En nuestro caso, el AUC es de 0.85, es decir, el área bajo toda la curva azul es de 0.85. El máximo sería 1, y supondría un cuadrado que cubriera todo el gráfico. Dicho de otro modo, cuanto más se pegue la curva a la esquina superior izquierda (0,1), mejor modelo tendremos.
- Hemos comentado antes que, para el umbral de 0.5 que hemos utilizado, nuestra sensibilidad era de 0.56. Si buscamos en el eje Y (sensibilidad) ese valor y trazamos desde ahí una línea vertical hacia abajo, cortará el eje X aproximadamente en 0.09, que es justo 1 menos la especificidad de nuestro modelo (0.91).
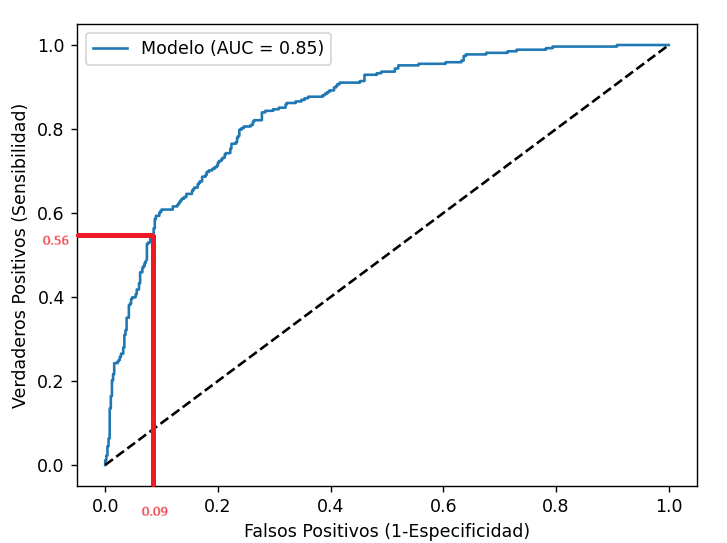
¿Cómo podríamos averiguar qué umbral es mejor para detectar más casos positivos y mejorar nuestro modelo? Esta curva ROC nos dice que podemos conseguirlo cambiando el umbral pero, al hacer esto, empeorará el eje X, es decir, "asustaremos a más gente sana". Esto es algo permisible en modelos basados en salud, para garantizar resultados buenos en aspectos críticos.
Conceptualmente el umbral óptimo correspondería con el punto de la curva que más se aleja de la diagonal de azar (en vertical). Suele corresponder con valores de Y altos (en torno a 0.80 o 0.85 al menos) que hacen que el eje X se desplace a la derecha también.
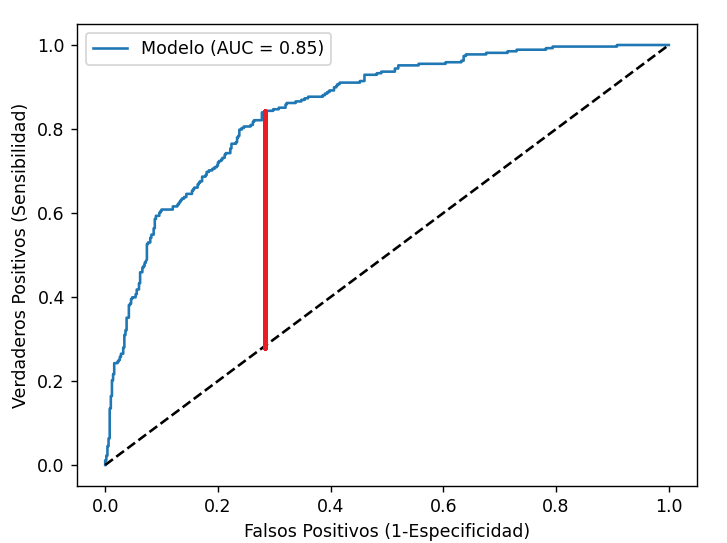
Aunque lo identifiquemos en la gráfica, no podemos extraer su valor a partir de ella, sino que podemos calcularlo así:
# Obtenemos los componentes de la curva
fpr, tpr, thresholds = roc_curve(y, y_pred)
# Calculamos el Índice de Youden para cada umbral
j_scores = tpr - fpr # (tpr es sensibilidad, fpr es 1-especificidad)
indice_optimo = np.argmax(j_scores)
umbral_optimo = thresholds[indice_optimo]
print(f"El umbral óptimo según Youden es: {umbral_optimo:.4f}")
print(f"Con este umbral, la Sensibilidad sube a: {tpr[indice_optimo]:.2f}")
print(f"Y la Especificidad se queda en: {1 - fpr[indice_optimo]:.2f}")
Conclusión y posibles mejoras
Nuestro modelo es conservador: prefiere decir que un paciente está sano a aventurarse a decir que tiene diabetes. Esto en medicina es problemático, porque el coste de no tratar la diabetes a tiempo puede ser muy caro, y compensaría más detectar más casos positivos aun a costa de "asustar" a otros pacientes y tenerles que hacer pruebas adicionales para descartarlo más adelante.
Algunas opciones para mejorar los resultados podrían ser:
- Bajar el umbral de positivo, de 0.5 a otro menor (por ejemplo 0.29 o algo así, que daría en el ejemplo anterior)
- Balancear los pesos de las clases en el dataset: hay muchos más casos negativos que positivos, y eso puede empujar al modelo a preferir decir que los pacientes no son diabéticos para acertar en la mayoría de casos.
- Cambiar el optimizador o reajustar otros parámetros para mejorar los resultados
Ejercicio 5
Aplica esto mismo en el ejercicio del cáncer de mama que hiciste en un documento anterior y saca las conclusiones oportunas.
Incluir métricas en la compilación
Es posible incluir algunas de estas métricas como parámetro metrics al compilar el modelo, para que se calculen en cada epoch. Debemos importar el paquete metrics de Keras y añadir las que nos interesen en dicho parámetro. Por ejemplo:
from keras import metrics
...
modelo.compile(
loss='binary_crossentropy',
...
metrics=[
'accuracy',
metrics.Precision(name='precision'),
metrics.Recall(name='recall'),
metrics.AUC(name='auc')
]
)
Con esto podremos ver la evolución de estos valores en cada epoch. Aunque, como hemos visto, podemos obtenerlos todos al final desde SKLearn, con lo que este paso es más opcional.
Epoch 200/200
1/20 ━━━━━━━━━━━━━━━━━━━━ 0s 26ms/step - accuracy: 0.7500 - auc: 0.8965 - loss: 0.4748 - precision: 20/20 ━━━━━━━━━━━━━━━━━━━━ 0s 5ms/step - accuracy: 0.7541 - auc: 0.8176 - loss: 0.4958 - precision: 0.6962 - recall: 0.5164 - val_accuracy: 0.7597 - val_auc: 0.8557 - val_loss: 0.4830 - val_precision: 0.7500 - val_recall: 0.4909
3.2. Clasificadores no binarios¶
Volvamos ahora al ejemplo de los coches que hemos estado haciendo. ¿Cómo se adaptan todas estas métricas en el caso de un clasificador no binario?
Para empezar, importaremos los mismos métodos de SKLearn, y también Seaborn si queremos mostrar algún mapa de calor con la matriz de confusión
import seaborn as sns
from sklearn.metrics import confusion_matrix, classification_report, auc, roc_curve
Matriz de confusión
Para crear la matriz de confusión seguimos unos pasos ligeramente distintos a un clasificador binario: en este caso tenemos que averiguar qué salida de y ha sido la de mayor probabilidad, y cotejar esa con la salida real de cada registro de entrada.
# 1. Obtener predicciones
y_pred_probs = modelo.predict(X)
y_pred_classes = np.argmax(y_pred_probs, axis=1)
y_true_classes = np.argmax(y.values, axis=1)
# Nombres de las categorías (importante mantener el orden de get_dummies)
nombres_clases = y.columns
# 2. Matriz de Confusión
cm = confusion_matrix(y_true_classes, y_pred_classes)
plt.figure(figsize=(8,6))
sns.heatmap(cm, annot=True, fmt='d', xticklabels=nombres_clases,
yticklabels=nombres_clases)
plt.xlabel('Predicción')
plt.ylabel('Real')
plt.title('Matriz de Confusión Multiclase')
plt.show()
Obtenemos una matriz como la siguiente:
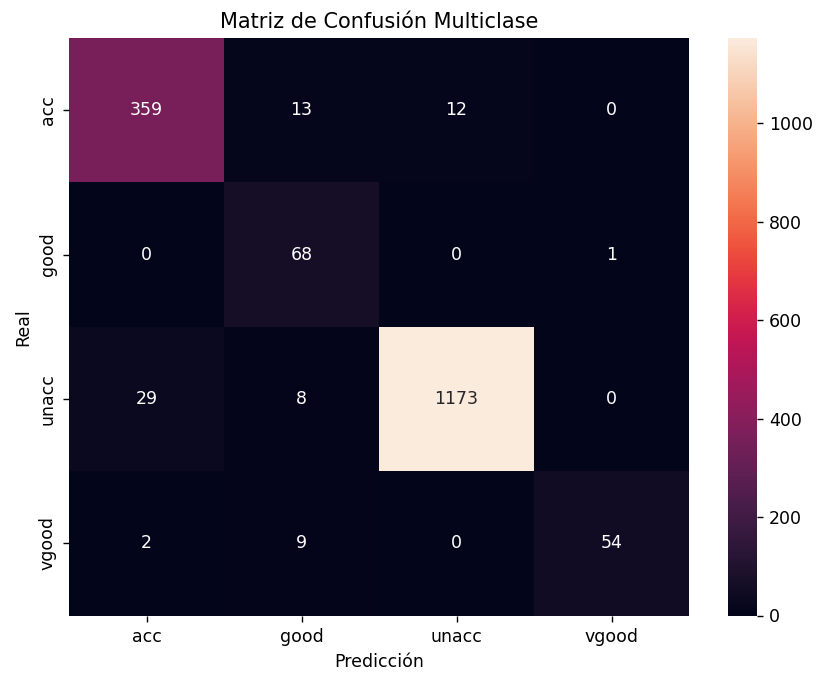
Como vemos, es una matriz N x N, siendo N el número de categorías de salida. En la diagonal principal tenemos lo mismo que en la otra (cuántos casos se han identificado correctamente de cada categoría). En el resto de casillas vemos cuántos casos de una categoría real se han confundido con otra predicha. Por ejemplo, 13 vehículos etiquetados como aceptables (acc) en la realidad se han predicho como buenos (good). Serían falsos positivos para la clase good. Lo mismo ocurre con el resto de casillas fuera de la diagonal.
Informe de clasificación
En cuanto al informe de clasificación donde se ven el resto de medidas estadísticas (sensibilidad, precisión, etc), quedaría así:
print("\nInforme de Clasificación:")
print(classification_report(y_true_classes, y_pred_classes,
target_names=nombres_clases))
Y obtendíamos un resultado como este:
precision recall f1-score support
acc 0.92 0.93 0.93 384
good 0.69 0.99 0.81 69
unacc 0.99 0.97 0.98 1210
vgood 0.98 0.83 0.90 65
accuracy 0.96 1728
macro avg 0.90 0.93 0.91 1728
weighted avg 0.96 0.96 0.96 1728
Analizamos estos resultados:
- La exactitud general del modelo (accuracy) es del 96%
- Vemos que el F1 Score para casos inaceptables es del 98%, ya que la precisión es del 99% y la sensibilidad del 97%. Esto significa que detecta casi todos los casos inaceptables reales (sensibilidad), y casi todos los que ha etiquetado como inaceptables realmente lo eran.
- El punto débil del modelo está en la etiqueta good. La sensibilidad es casi perfecta (99% de casos reales detectados), pero la precisión es del 69% (hay un 31% de casos que ha marcado como buenos y que realmente no lo eran).
- En el caso de los clasificadores múltiples, las métricas de macro avg y weighted avg son aún más importantes. En este caso vemos que el weighted avg es ligeramente mayor porque el sistema detecta muy bien los casos predominantes (unacc). Sin embargo con el macro avg se reduce el resultado por los fallos que hay en algún caso minoritario, como hemos visto que ocurre con los casos good.
Curva ROC y área bajo la curva (AUC)
A la hora de calcular la curva ROC en un modelo multi-categoría el sentido de esta curva cambia. No es una sola línea, ya que hay múltiples categorías, y se calcula una curva para cada clase comparándola con el resto.
# Gráfico de Curvas ROC Multiclase
plt.figure(figsize=(10, 8))
for i in range(num_clases):
fpr, tpr, _ = roc_curve(y.values[:, i], y_pred_probs[:, i])
roc_auc = auc(fpr, tpr)
plt.plot(fpr, tpr, label=f'ROC {nombres_clases[i]} (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], 'k--')
plt.xlabel('Tasa Falsos Positivos')
plt.ylabel('Tasa Verdaderos Positivos')
plt.title('Curvas ROC por Clase (One-vs-Rest)')
plt.legend()
plt.show()
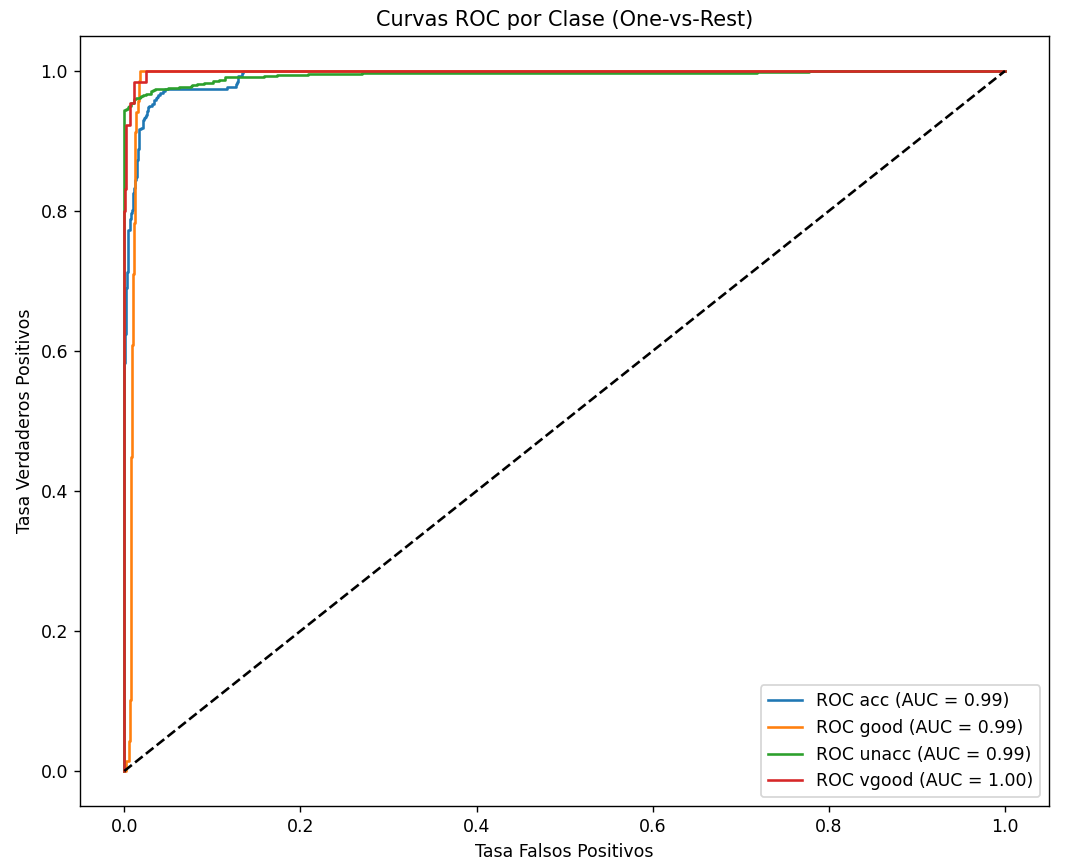
Si quisiéramos reajustar el umbral de cualquier categoría para captar más casos positivos de la misma, bastaría con usar la fórmula matemática que hemos aplicado en el caso binario, con el tpr y fpr calculado para esa categoría.
Nota
En este caso hemos empleado la función auc de sklearn.metrics en lugar de roc_auc_score como en el caso anterior. En realidad podemos emplear cualquiera de las dos:
auces más matemática, no necesita ningún modelo, sino simplemente las tasas de falsos positivos y verdaderos positivos en cuestión (fprytpr), y se emplea para medir el área bajo cualquier curva con esos datos ya calculados.roc_auc_scoretrabaja sobre los valores predichos de y y los reales del modelo, y calcula el AUC a partir de ellos.
3.3. Modelos de regresión¶
Para modelos de regresión todas estas estadísticas adicionales (sensibilidad, precisión, etc) no existen. Podemos incluir en el parámetro metrics de la compilación las métricas que queremos calcular:
modelo.compile(
optimizer='adam',
loss='mse', # La pérdida que el modelo intenta minimizar
metrics=['mae', 'mse'] # Métricas para monitorizar
)
Además de las funciones de coste que queramos monitorizar (MAE, MSE, etc), quizá puede ser interesante calcular el gráfico de dispersión entre los valores reales y los predichos, para ver gráficamente si están ajustados a la recta de 45º (buena precisión) o se alejan de ella. Podríamos plantearlo así:
# Obtener las predicciones del modelo
y_pred = modelo.predict(X_test).flatten() # Aplanamos por si Keras devuelve (n, 1)
# Dibujamos los puntos
plt.scatter(y_test, y_pred, alpha=0.5, color='blue', label='Predicciones')
# Dibujamos la línea de "Perfección" (donde Real = Predicho)
limite_max = max(max(y_test), max(y_pred))
limite_min = min(min(y_test), min(y_pred))
plt.plot([limite_min, limite_max], [limite_min, limite_max],
color='red', linestyle='--', linewidth=2, label='Referencia Ideal (y=x)')
# Personalización
plt.title('Regresión: Real vs Predicho')
plt.xlabel('Valores Reales')
plt.ylabel('Valores Predichos por el Modelo')
plt.legend()
plt.grid(True)
plt.show()
Ejercicio 6
Retoma el modelo que predecía la presión sanguínea alta de un paciente en base a otros parámetros, que hemos planteado en este documento anterior, y muestra el gráfico de dispersión de los valores reales y los predichos.
IMPORTANTE: para que el gráfico de regresión salga correcto, debes eliminar los valores anómalos que hay en la columna objetivo: quita todas las filas cuya presión ap_hi exceda de 200 o sea negativa.
4. Ajuste de hiperparámetros¶
En un modelo de machine o deep learning existen una serie de parámetros (normalmente los datos de entrada que proporcionamos al modelo, y que no son configurables) y de hiperparámetros. Estos últimos son elementos inherentes al modelo que sí se pueden configurar. En el caso de las redes neuronales, podríamos hablar de la configuración de la red (número de capas), optimizadores, funciones de activación, etc.
Ahora que ya tenemos unas nociones un poco más extensas de lo que supone trabajar con una red neuronal, hagamos un resumen de los hiperparámetros que tenemos que considerar a la hora de ajustar lo mejor posible el funcionamiento de dicha red:
- El número de capas ocultas necesarias, y el tamaño (número de neuronas) de las mismas
- Función de activación más adecuada en cada capa
- Función de coste (loss) elegida al compilar el modelo
- Optimizador elegido (también al compilar), junto con su learning rate
- Tamaños de los conjuntos de entrenamiento y test
- Número de iteraciones (epochs) recomendables, y tamaño del batch
- Necesidad de capas de dropout, y dónde ubicarlas
4.1. Capas ocultas y funciones de activación¶
¿Qué beneficios aporta añadir más capas ocultas a una red neuronal? ¿Y cuántas neuronas debería tener cada capa? Son preguntas sin una respuesta fija o concreta, pero hay algunas cuestiones que debemos tener en cuenta para ayudarnos a tomar una decisión.
Respecto al número de capas ocultas recomendable, debemos tener en cuenta que, en problemas que sean linealmente separables, no es necesaria ninguna capa oculta. Podemos conectar todas las entradas a la(s) neurona(s) de salida para obtener un resultado, que será una combinación lineal de las entradas multiplicadas por los pesos.

Sin embargo, en la gran mayoría de los casos, los datos de entrada son interdependientes, y afectan a la salida de una forma más compleja. Añadir capas ocultas nos permite detectar estas interdependencias entre parámetros de entrada. Así, cada neurona de una capa oculta puede aprender una característica diferente sobre los datos de entrada y, al añadir más capas, permitimos definir distintos niveles de abstracción sobre los datos de entrada, capturando primero rasgos más generales para luego, en otras capas, detectar elementos más específicos.
En cuanto al número de neuronas en cada capa, también es un parámetro que dependerá del problema en cuestión. Una capa con pocas neuronas puede caer en el underfitting, es decir, no llegar nunca a realizar estimaciones acertadas, ni en el conjunto de entrenamiento ni en el de test. Por otra parte, un número excesivo de neuronas puede llevar al caso opuesto, como hemos visto: el overfitting. Tener tanta cantidad de conexiones disponibles puede permitir a la red memorizar un camino distinto para cada posible valor de entrada de los datos de entrenamiento, y así memorizarlos todos. Por lo tanto, es conveniente definir un número adecuado. Como hemos comentado con anterioridad, existen varias teorías al respecto:
- Un tamaño entre el tamaño de entrada y el de salida
- La media de las dos capas (entrada y salida)
- 2/3 de la capa de entrada más la de salida
- Un tamaño inferior al doble de la capa de entrada
- ...
Se pueden probar varias de estas posibilidades y quedarnos con la que mejor resultado ofrezca.
Además de establecer el número adecuado de capas ocultas y tamaño de las mismas, es conveniente elegir una función de activación apropiada en cada capa. Si utilizamos funciones de activación no lineales en diferentes capas, aumentamos la flexibilidad de las mismas. En general, podemos afirmar que cualquier red neuronal de 2 capas ocultas con una función de activación no lineal (incluyendo ReLU), y con suficientes neuronas en las capas ocultas, es capaz de expresar cualquier mapeo de entrada a salida. En este sentido, recuerda que:
- La función de activación ReLU nos puede servir para provocar un efecto de "desactivación" en las neuronas. Aquellas que no lleguen a un valor apropiado no emitirán una salida a la capa siguiente. Esto puede ser útil para que, dependiendo de los valores de entrada, se transmitan unos datos u otros a las capas siguientes. Es la función de activación más utilizada en las capas ocultas.
- Las funciones de activación sigmoide y tangente hiperbólica nos servirán para acotar los valores de salida entre 0 y 1 o entre -1 y 1, respectivamente. No son habituales en las capas ocultas, y suelen emplearse más en las capas de salida.
- La función de activación softmax define una distribución probabilística, es decir, la probabilidad de que el elemento de la entrada pertenezca a una de las categorías definidas en la salida. También suele emplearse en la capa de salida principalmente.
- La función lineal se emplea en operaciones de regresión, para dar un valor de salida de entre un conjunto de datos continuos.
4.2. Eligiendo la función de coste¶
La función de coste o pérdida ayudará a determinar lo bien o mal que la red está realizando sus cálculos, comparándolos con los resultados reales que se deberían obtener (aprendizaje supervisado). En este sentido, podemos distinguir dos grandes grupos de funciones de coste:
- Para tareas de regresión (es decir, predecir un valor de salida en base a unos datos de entrada), usaremos funciones de coste que calculen la diferencia entre los valores reales y los valores predichos. Aquí podemos utilizar funciones como el error absoluto medio (MAE), o el error cuadrático medio (MSE), que hemos explicado en documentos anteriores. Sin embargo, cuando los valores son elevados o las diferencias pueden ser grandes, estas funciones pueden dar un valor muy grande. En estos casos podemos emplear el coste logarítmico (MSLE), que reduce estas diferencias. También podemos optar por las raíces cuadradas de los errores anteriores (RMSE, RMSLE), aunque estas últimas no están disponibles directamente en Keras/Tensorflow, y tenemos que implementarlas de forma manual.
- Para tareas de clasificación (definir a qué categoría pertenece el elemento de la entrada en base a sus valores), podemos distinguir entre clasificaciones binarias (dividir el conjunto de entrada en dos categorías) o clasificadores múltiples. En el primer caso, bastará con una única neurona de salida, y es conveniente utilizar una función de entropía cruzada binaria (binary_crossentropy), junto con una función de activación sigmoide en la capa de salida. En el caso de clasificaciones múltiples, utilizaremos una neurona de salida por cada categoría, función de coste de entropía cruzada categórica (categorial_crossentropy) y una función de activación softmax en cada neurona de la capa de salida.
4.3. Eligiendo el optimizador y el learning rate¶
Como hemos visto, los optimizadores ayudan a disminuir más rápidamente la función de coste, buscando el mínimo de la función. Keras/Tensorflow incorpora algunos optimizadores predefinidos. En todos ellos es crucial ajustar bien la tasa de aprendizaje o learning rate. Este hiperparámetro define cómo de grandes o pequeños son los "saltos" que damos en la gráfica en busca del mínimo. Como ya hemos visto anteriormente, un valor muy pequeño puede hacer que el modelo tarde demasiado en encontrar el mínimo, o que se quede estancado en un mínimo local y no sea capaz de llegar a otras partes de la gráfica. Por contra, un valor muy grande puede hacer que los saltos que se dan en la gráfica del coste sean demasiado largos, y no se llegue nunca a "afinar" para encontrar ese mínimo.
Algunos de los optimizadores más populares actualmente son:
- SGD (descenso de gradiente estocástico)
- RMSprop (Root Mean Squared Propagation, propagación de la raíz media de los cuadrados)
- Adam
- Adagrad
- Adadelta
- ...
¿Cuál de todos estos optimizadores utilizar? Nuevamente, dependerá del problema en cuestión, aunque la mayoría de ellos se ajustan bien con alguno de la terna SGD / Adam / RMSProp. En general se diferencian en la forma de definir la dirección de optimización. Algunos, como SGD, son más rígidos, y no funcionan tan bien cuando la diferencia de gradiente es mayor en una dimensión que en otra. Otros, como Adam, son más flexibles o adaptativos, y suelen dar mejores resultados con conjuntos grandes de datos, o ruido que hace que sea difícil encontrar el camino al mínimo.
En el caso de Keras, disponemos de estos optimizadores y otros más en el paquete keras.optimizers (más información aquí). Podemos utilizarlos poniendo directamente su nombre en el parámetro optimizer del método compile, o bien instanciando la clase correspondiente. En este último caso, podemos ajustar manualmente el learning rate. De lo contrario, se asume un valor por defecto de 0.001, normalmente.
# Primera alternativa
modelo.compile(loss='mse', optimizer='adam')
# Segunda alternativa
opt = keras.optimizers.Adam(learning_rate=0.01)
modelo.compile(loss='mse', optimizer=opt)
4.4. Otros parámetros¶
Además de todos los elementos anteriores, también tenemos que considerar el ajuste de otros parámetros de la red, como son:
-
El tamaño de los conjuntos de entrenamiento y test. En este caso, la horquilla suele moverse entre un 15% y un 30% para test, y el resto para entrenamiento. Todo dependerá, principalmente, de la cantidad de datos que tengamos disponibles. Si son muchos, podemos permitirnos destinar un 30% a test. Pero si son pocos, conviene acortar el conjunto de test para permitir que la red entrene mejor con más datos disponibles
-
El número de iteraciones (epochs). Esto también va a depender de cada proceso, y podemos analizarlo con la curva del coste (loss) y/o la exactitud (accuracy). En cuanto veamos que la pendiente se aplana y estabiliza, es que la red ya tiene poco más que aprender, y no son necesarias muchas más iteraciones. También es cierto que algunos de los parámetros anteriores, como el número de capas ocultas o la cantidad de neuronas, influyen en que esta convergencia sea más o menos rápida.
-
El tamaño del batch. No suele ser un parámetro excesivamente relevante, e incluso el valor por defecto que asigna Keras (32) es aceptable. Si el conjunto de datos es reducido, podemos también acortar el tamaño del batch a 24 o 16, por ejemplo, para facilitar más iteraciones por epoch y acelerar el aprendizaje. Aunque, como hemos explicado con anterioridad, un tamaño de batch excesivamente pequeño puede provocar que los pesos no se ajusten adecuadamente en esa sub-iteración, y el aprendizaje sea entonces más lento o menos exitoso.
-
Las capas de Dropout. Este parámetro dependerá del overfitting que tenga la red. Si detectamos ese overfitting, podemos optar por ir añadiendo capas de Dropout entre capas ocultas de nuestra red para desconectar un porcentaje de neuronas (normalmente entre el 10% y el 30% aproximadamente) y estudiar el efecto que produce. Recuerda que, además de esto, también podemos optar por reducir el tamaño de la red, o aplicar una estrategia de early stopping para hacer que se detenga en cuanto empiece el overfitting de forma automática.
4.5. Conclusiones¶
Como podemos concluir en base a lo que hemos visto hasta ahora, no existe una ciencia exacta, ni unos pasos fijos recomendables a seguir para ajustar los hiperparámetros de nuestra red neuronal. Hay que conocer bien el problema a resolver para poder establecer adecuadamente algunos de ellos (como las funciones de activación y coste), y luego conviene probar varias combinaciones de otros (número de capas ocultas, optimizador, learning rate...) hasta dar con la que obtenga mejores resultados.
Ejercicio 7
Vamos a subir el dataset sobre estimaciones de coches que hemos empleado en ejemplos anteriores a Google Colab. Y completaremos este documento para probar distintas configuraciones de redes neuronales. Sigue los pasos indicados en el documento Colab y determina cuál de todas las opciones es la que ofrece mejores resultados. También puedes probar tus propios experimentos.