Programación lógica¶

En este documento vamos a abordar el paradigma de la programación lógica, mediante el cual podremos definir problemas basados en reglas, de modo que estas reglas se aplican automáticamente por parte del programa. Veremos los principios básicos del paradigma, y en qué aspectos de la inteligencia artificial puede resultar útil.

1. Principios de la programación lógica¶

La programación lógica es un paradigma de programación declarativo, es decir, indicamos las características del problema a resolver, en lugar de los pasos a dar para resolverlo. Además, es un paradigma basado en reglas y hechos:

Los hechos (facts en inglés) son aserciones que se consideran ciertas sobre los datos que intervienen en un problema. Por ejemplo, si decimos Juan es el padre de Lucía, es un hecho de nuestro problema.
Las reglas son las restricciones que debe cumplir el problema para encontrar una solución o sacar conclusiones. Por ejemplo, podemos definir que dos personas son hermanas si tienen el mismo padre/madre.

Por tanto, en programación lógica definiremos los hechos conocidos del problema y las reglas que se deben cumplir a la hora de generar nuevo conocimiento o sacar ciertas conclusiones. Una vez definida esta base de conocimiento, formularemos preguntas al sistema para obtener respuestas, partiendo de esa base. El esquema que se sigue se puede representar de este modo:

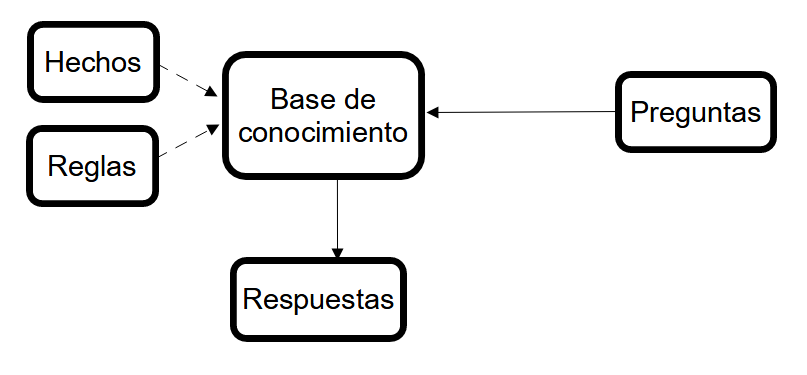
1.1. Un ejemplo introductorio¶

Como decimos, la programación lógica se basa en hechos y reglas, sobre las que luego se formulan preguntas. Por ejemplo, imaginemos que queremos establecer relaciones de parentesco, como haremos en un ejemplo posterior:

Los hechos son datos que ya se conocen de antemano. Por ejemplo, podríamos decir que Juan es hijo de Pedro, y que Silvia es hija de Juan.
Las reglas permiten generar nuevo conocimiento a partir de lo que ya sabemos. Por ejemplo, podemos definir una regla por la que se establece que una persona es nieto/a de otra si es hijo/a de su hijo/a.
Las preguntas se basan en los hechos y las reglas para obtener respuestas a cosas que no se conocen. Podríamos preguntar cosas simples, como quién es el hijo de Pedro (Juan), o cosas algo más elaboradas, como quién es el nieto/a de Pedro (Silvia).

2. Programación lógica en Python¶

Existen algunas librerías en Python para trabajar con programación lógica, tales como:

logpy, una librería que incorpora diferentes módulos con funcionalidades de programación lógica, tales como hechos, reglas, relaciones. Es bastante completa, pero ha quedado algo obsoleta, ya que no tiene mantenimiento en los últimos años. Aquí podemos consultar su repositorio oficial.
pytholog, una librería que incorpora la sintaxis del lenguaje de programación Prolog, para poderla usar desde Python. Sin embargo, hay algunas características de dicho lenguaje que no están del todo incorporadas, lo que limita bastante su uso. Aquí podemos consultar su documentación oficial.
kanren, una librería que se originó como una rama alternativa a logpy, y que dispone de mantenimientos y actualizaciones más recientes. Dispone de una versión más reducida y actualizada, llamada minikanren, que será la que utilicemos en estos apuntes. Aquí podemos consultar la documentación oficial.

Lo primero que deberemos hacer es instalar la librería con el correspondiente comando pip:

pip install miniKanren

A la hora de importar la librería en nuestros programas, es habitual elegir qué elementos concretos nos van a hacer falta. Algunos de los más habituales son:

facts: para definir los hechos ciertos de nuestro espacio de conocimiento
Relation: para definir relaciones entre los componentes de nuestra base de conocimiento
run: para ejecutar acciones en el programa. Típicamente, formular preguntas a nuestra base de conocimiento para recoger las respuestas
Otros elementos útiles pueden ser conde, eq o var, para establecer comprobaciones entre datos, como veremos en algún ejemplo posterior.

Aquí vemos un posible ejemplo de importación de la librería

from kanren import run, var, eq, conde, Relation, facts

2.1. Un ejemplo sencillo: relaciones de parentesco¶

Imaginemos que queremos representar algunas de las relaciones de parentesco que se puedan dar en un árbol genealógico como el siguiente:

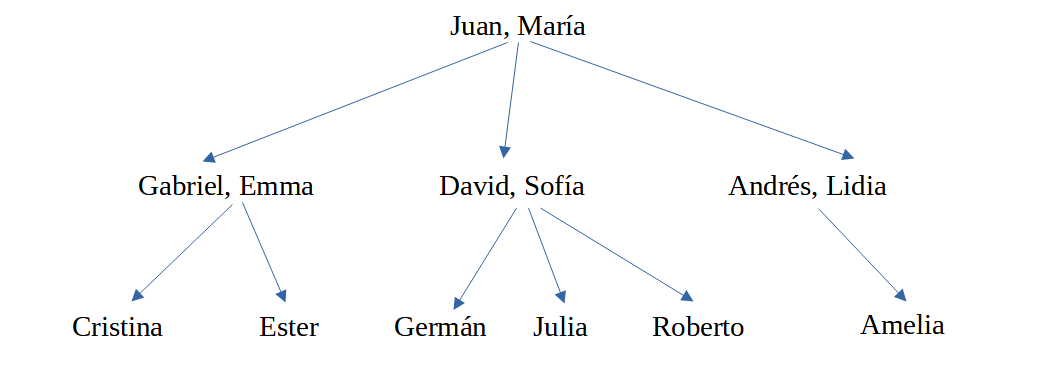
Deberemos plantear una serie de hechos y reglas que nos permitan extraer o comprobar la información de dicho árbol. Este conjunto de hechos y reglas es lo que se conoce como base de conocimiento de nuestro sistema (en inglés, knowledge base).

En primer lugar, vamos a definir una serie de hechos en esta base de conocimientos. Comenzaremos definiendo dos relaciones básicas: las de padre y madre, y en la base de hechos añadiremos quién es padre de quién, y quién es madre de quién, de este modo:

padre = Relation()
madre = Relation()

facts(padre, ("Juan", "Gabriel"),
             ("Juan", "David"),
             ("Juan", "Lidia"),
             ("Gabriel", "Cristina"),
             ("Gabriel", "Ester"),
             ("David", "German"),
             ("David", "Julia"),
             ("David", "Roberto"),
             ("Andrés", "Amelia")
     )
facts(madre, ("Maria", "Gabriel"),
             ("Maria", "David"),
             ("Maria", "Lidia"),
             ("Emma", "Cristina"),
             ("Emma", "Ester"),
             ("Sofia", "German"),
             ("Sofia", "Julia"),
             ("Sofia", "Roberto"),
             ("Lidia", "Amelia")
     )

Estos hechos pueden leerse del siguiente modo, por ejemplo: *Juan es el padre de Gabriel", "Emma es la madre de Ester"...

Sobre esta base podemos hacer preguntas simples. Por ejemplo, podemos preguntar quién es la madre de Roberto (debería indicarnos que es Sofia). Para ello usamos el método run, al que le pasaremos los siguientes parámetros:

El número de elementos que esperamos como respuesta (pondremos 0 si no queremos limitar)
La variable que emplearemos para almacenar cada una de las respuestas válidas
Los predicados que deben cumplirse

Por ejemplo, la pregunta anterior (quién es la madre de Roberto) la podemos formular así:

x = var()
print(run(1, x, madre(x, "Roberto")))

Sobre esta base de hechos podemos definir reglas que nos permitan deducir conocimientos algo más complejos. Por ejemplo, podemos definir reglas que nos determinen los progenitores de una persona. Un progenitor de una persona x será cualquier persona que sea o bien su padre o bien su madre. Añadimos estas reglas a través de funciones en Python:

def progenitor(p, x):
    return conde([padre(p, x)], [madre(p, x)])

Notar que, en este caso, el progenitor puede ser uno u otro (padre o madre). Usamos el operador conde de kanren, que representa a los operadores and y or:

En este caso le pasamos dos listas con reglas separadas, lo que significa que los elementos que cumplan las condiciones de una u otra lista (or) forman parte del resultado.
Si sólo pasamos una lista con varias reglas, el resultado lo formarán los elementos que cumplan todas las reglas de esa lista (and).

Podemos preguntar por los progenitores de Roberto, obteniendo esta respuesta:

print(run(2, x, progenitor(x, "Roberto")))
# ("David", "Sofia")

Notar como, en este caso, al método run le pasamos como primer parámetro un 2, indicando que buscamos dos resultados. Si pasamos un 1 mostraría el primero de los progenitores que encontrara, y si pasamos 0 obtendría todos los progenitores que encontrara.

Otras reglas más complejas nos pueden servir para determinar los abuelos de una persona. Un abuelo/a de una persona x será el progenitor/a de su progenitor/a:

def abuelo(a, x):
    y = var()
    return conde([progenitor(a, y), progenitor(y, x)])

En este caso, usamos una variable auxiliar intermedia y para representar el hecho de que buscamos a los elementos a que sean progenitores de aquellos y que a su vez sean progenitores del elemento en cuestión x. Preguntemos por los abuelos de Ester, o de quién es abuela Maria obteniendo estas respuestas:

print(run(2, x, abuelo(x, "Ester")))
# ("Maria", "Juan")
print(run(0, x, abuelo("Maria", x)))
# ('Cristina', 'Julia', 'Amelia', 'Ester', 'Roberto', 'German')

Notar como, en el segundo caso, pasamos 0 como primer parámetro de run, porque no sabemos cuántos resultados vamos a obtener, pero queremos obtenerlos todos.

Finalmente, añadiremos la regla para obtener los hermanos de una persona:

def hermano(h, x):
    p = var()
    return conde([progenitor(p, h), progenitor(p, x), neq(h, x)])

Lo que hacemos en este caso es buscar aquellos elementos x que tengan un progenitor p igual al que estamos buscando, y que no sean él mismo (neq(h, x)). La operación neq la deberemos importar de kanren.constraints.

Hay que tener en cuenta que, al consultar a esta regla, obtendremos resultados duplicados (los hermanos aparecerán una vez por parte del padre y otra por parte de la madre), así que podemos convertir el resultado en un conjunto con set, para eliminar esos duplicados. Así obtendríamos los hermanos de Ester:

print(set(run(0, x, hermano("Ester", x))))
# {Cristina}

Ejercicio 1

Copia el código completo de los ejemplos anteriores en un archivo llamado Parentesco.py, y añade una regla para obtener los primos de una persona. Dos personas X e Y son primos si alguno de sus progenitores son hermanos.

Solución Ejercicio 1

Aquí puedes ver un vídeo con la solución paso a paso del ejercicio.

3. Aplicaciones prácticas de la programación lógica¶

La programación lógica es un paradigma con un ámbito de uso bastante limitado hoy en día. Aún así, se puede aplicar en problemas de distintos tipos.

3.1. Problemas de satisfacción de restricciones¶

Los problemas de satisfacción de restricciones consisten en hallar una solución a un problema cumpliendo una serie de requisitos o restricciones. Veamos algunos ejemplos:

El problema de la oveja, la col, el lobo y el granjero que deben cruzar un río. El granjero debe transportar al resto de elementos en una barca donde sólo cabe un elemento más, con la restricción de no dejar solos en la misma orilla a la oveja y la col (porque la oveja se comería la col), ni al lobo y la oveja (porque el lobo se comería a la oveja). Dependiendo del lenguaje que se utilice se puede resolver de varias formas. En Prolog, por ejemplo, definimos las reglas a cumplir y generamos la secuencia de pasos que se deben dar, cumpliendo esas reglas. Aquí podemos ver un ejemplo. En Python también se puede resolver usando librerías como Kanren, o también directamente, como en este ejemplo.
Otros problemas similares también pueden plantearse, como aquellos en los que nos dan una serie de afirmaciones incompletas y debemos responder a preguntas que quedan pendientes. Aquí tenemos un ejemplo.
El problema del coloreado de mapas. Consiste en, dado un mapa con un conjunto de regiones, colorearlas de forma que dos regiones adyacentes tengan colores diferentes entre ellas. Veremos cómo resolver este tipo de problemas a continuación.
El problema de las N reinas, que consiste en colocar N reinas en un tablero de ajedrez de forma que ninguna de ellas se vea atacada por las demás. Aquí vemos un ejemplo de solución con Prolog.

3.2. Definición de sistemas expertos¶

Los sistemas expertos básicamente acumulan una (gran) cantidad de conocimiento que, en base a unos parámetros de entrada y unas reglas predefinidas, aplican para encontrar una solución. Ejemplos claros pueden ser los sistemas de ayuda al diagnóstico médico en los que, a partir de la sintomatología del paciente determinan posibles patologías que pudiera tener. También los sistemas de ayuda a la inversión o asistentes para concesión de préstamos analizan una serie de valores de entrada y, aplicando una serie de reglas sobre ellos, determinan la idoneidad de la inversión o de la concesión del préstamo.

En un ambiente más lúdico, podemos emplear la programación lógica para elaborar ciertos juegos que gestionen también una base de conocimiento. Un ejemplo puede ser el conocido juego Akinator, del asistente Alexa, en el que el sistema trata de adivinar el personaje en el que estamos pensando, a través de una serie de preguntas que básicamente ayudan a descartar candidatos: ¿Es un personaje imaginario?, ¿Sale en televisión?, ¿Es un deportista?...

3.3. Ejemplo: coloreado de mapas¶

Imaginemos que tenemos un mapa con diferentes regiones, y queremos utilizar colores diferentes para pintar regiones que sean adyacentes. Imaginemos que sólo disponemos de un conjunto de colores limitado (por ejemplo, rojo, azul y verde), de modo que debemos elegir bien la estrategia a seguir para no repetir colores en zonas adyacentes.

Pongamos, por ejemplo, el mapa de las provincias de Castilla La Mancha:

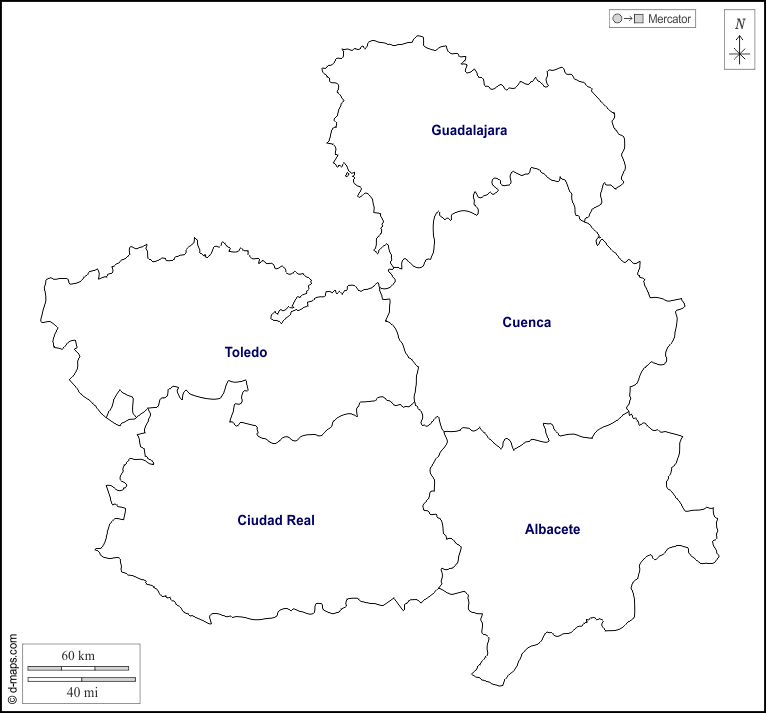
Podemos definir en nuestra base de conocimientos los colores diferentes que utilizaremos. Usaremos la relación distinto para indicar diferencias entre colores, y la regla diferente para hacer comprobaciones bidireccionales (si el rojo es distinto al azul, el azul también debe ser distinto al rojo).

from kanren import run, var, eq, conde, Relation, facts

distinto = Relation()

facts(distinto, ("Rojo", "Azul"),
                ("Rojo", "Verde"),
                ("Azul", "Verde")
     )

def diferente(c1, c2):
    return conde([distinto(c1, c2)], [distinto(c2, c1)])

Necesitaremos definir también una variable para guardar el color de cada una de las provincias:

cAB = var() # Albacete
cCR = var() # Ciudad Real
cCU = var() # Cuenca
cGU = var() # Guadalajara
cTO = var() # Toledo

Definimos ahora una regla que nos permita especificar un color para cada una de las cinco provincias. En este sentido, declaramos una variable para almacenar cada color: cAB (color de Albacete), cCR (color de Ciudad Real), cCU (color de Cuenca), cGU (color de Guadalajara) y cTO (color de Toledo). La regla buscará cualquier combinación de colores que cumpla con las restricciones de adyacencia, indicando que buscaremos colores diferentes para provincias adyacentes:

def colorear(cAB, cCR, cCU, cGU, cTO):
    return conde([diferente(cAB, cCR), diferente(cAB, cCU), diferente(cCR, cTO),
        diferente(cCR, cCU), diferente(cTO, cCU), diferente(cCU, cGU)])

Como podemos ver, hemos indicado que queremos un color diferente para Albacete y Ciudad Real, y también para Albacete y Cuenca, Ciudad Real y Toledo... indicando así todos los casos de adyacencia entre provincias.

Para obtener la solución, basta con preguntar:

print(run(1, [cAB, cCR, cCU, cGU, cTO], colorear(cAB, cCR, cCU, cGU, cTO)))

Notar que, en este caso, el segundo parámetro de run es una lista con las variables que queremos rellenar, y que le pasamos a la regla colorear. Como primer parámetro de run hemos indicado 1, con lo que nos devolverá la primera solución válida que encuentre, por ejemplo:

(['Azul', 'Rojo', 'Verde', 'Rojo', 'Azul'],)
#   AB      CR       CU      GU      TO

Sin embargo, si especificamos 0 como primer parámetro, obtendremos todas las posibles soluciones.

Notar también que, si hubiéramos especificado sólo dos colores en los hechos en lugar de tres, habríamos obtenido un resultado vacío, indicando que no se pueden cumplir las restricciones.

Ejercicio 2

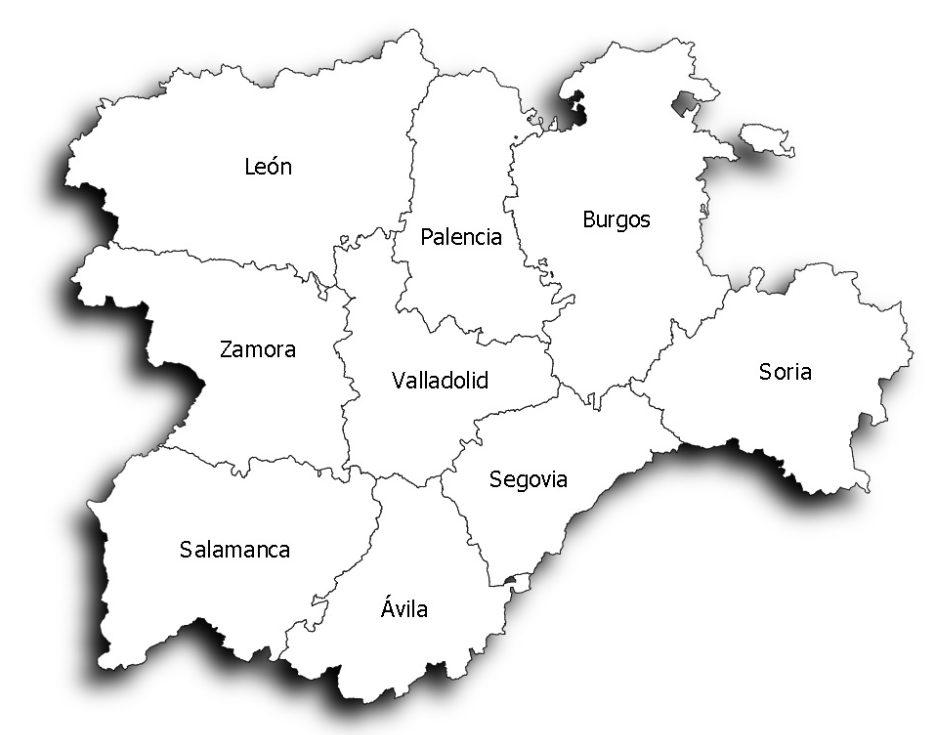
Adapta el ejemplo anterior al caso de las provincias de Castilla y León. Procura determinar el menor número de colores necesario para resolver la tarea. Procura que la salida especifique claramente qué color va en cada provincia. Por ejemplo:

Ávila - Verde
Burgos - Azul
León - Azul
Palencia - Verde
Salamanca - Amarillo
Segovia - Amarillo
Soria - Verde
Valladolid - Rojo
Zamora - Verde

Ejercicio 3

Vamos a desarrollar un sistema experto que ayude a diagnosticar enfermedades. La base de conocimiento de las enfermedades y sus sintomas la facilitaremos en un fichero de texto con un formato como éste:

resfriado:tos,mocos
gripe:tos,fiebre
faringitis:dolor de garganta,fiebre
coronavirus:tos,dificultad para respirar,fiebre
varicela:granos en el cuerpo,fiebre

En cada línea del fichero indicamos la enfermedad y, tras los dos puntos, los síntomas que tiene, separados por comas.

Se pide desarrollar un programa que use programación lógica para acumular como hechos los síntomas de cada enfermedad y luego le pregunte al usuario repetidamente qué síntomas tiene. El usuario irá eligiendo un síntoma tras otro de la lista de síntomas disponibles (los que haya en el fichero), y tras cada síntoma el sistema le dirá qué posibles enfermedades cuadran con los síntomas que ha descrito hasta ese momento. El programa finalizará cuando el usuario elija terminar, o cuando los síntomas que ha descrito no cuadren con ninguna enfermedad restante (o cuando cuadren sólo con una de ellas).

Aquí vemos un ejemplo de funcionamiento:

1. tos
2. dolor de garganta
3. dificultad para respirar
4. granos en el cuerpo
5. fiebre
6. mocos
Elige un síntoma, o 0 para terminar:
1
Posibles enfermedades: resfriado, coronavirus, gripe
Quieres continuar?(S/N): S
1. dolor de garganta
2. dificultad para respirar
3. granos en el cuerpo
4. fiebre
5. mocos
Elige un síntoma, o 0 para terminar:
4
Posibles enfermedades: coronavirus, gripe
Quieres continuar?(S/N): S
1. dolor de garganta
2. dificultad para respirar
3. granos en el cuerpo
4. mocos
Elige un síntoma, o 0 para terminar:
2
Posibles enfermedades: coronavirus