Redes neuronales convolucionales¶

Una red neuronal convolucional es un tipo de perceptrón multicapa empleado fundamentalmente para tareas de visión artificial. Su funcionamiento trata de asemejarse a las neuronas de la corteza visual primaria del cerebro humano y, de esta manera, podemos definir modelos especializados en tareas como identificación de elementos o clasificación de imágenes.

Los fundamentos de este tipo de red fueron propuestos por K. Fukushima en 1980, pero fue posteriormente Yann LeCun quien los perfeccionó, en 1989, enfocándolos a aplicaciones de visión por computador. Años más tarde, en 2012, Krizhevsky, Sutskever y Hinton publicaron una red llamada AlexNet que ganó un concurso de reconocimiento de imágenes usando esta tecnología. Notar que LeCun forma parte hoy en día del equipo de Facebook, y G. Hinton, que fue uno de sus mentores, ha formado parde del equipo de Google. Dicho de otro modo, las grandes tecnológicas mundiales cuentan o han contado en sus filas con algunos de los padres de las diferentes estrategias de redes neuronales existentes.

En los últimos años las RNC han ganado mucha popularidad, pues podemos aplicarlas a cosas tan actuales como los sistemas de conducción autónoma, para detectar en tiempo real los elementos que hay desde el punto de vista del conductor del vehículo, y hacer que éste reaccione en consecuencia. También en sistemas de reconocimiento de caras, como los sistemas de bloqueo de smartphones, se aplica este tipo de técnica.

1. Fundamentos de las RNC¶

Para empezar, veremos cuáles son los fundamentos teóricos en los que se apoyan las redes convolucionales. Explicaremos en qué consiste la operación de convolución y cómo se aplica sobre imágenes para detectar patrones u objetos. También veremos cómo recopilar luego toda la información extraída para emitir un resultado final sobre el análisis de la imagen.

1.1. La operación de convolución¶

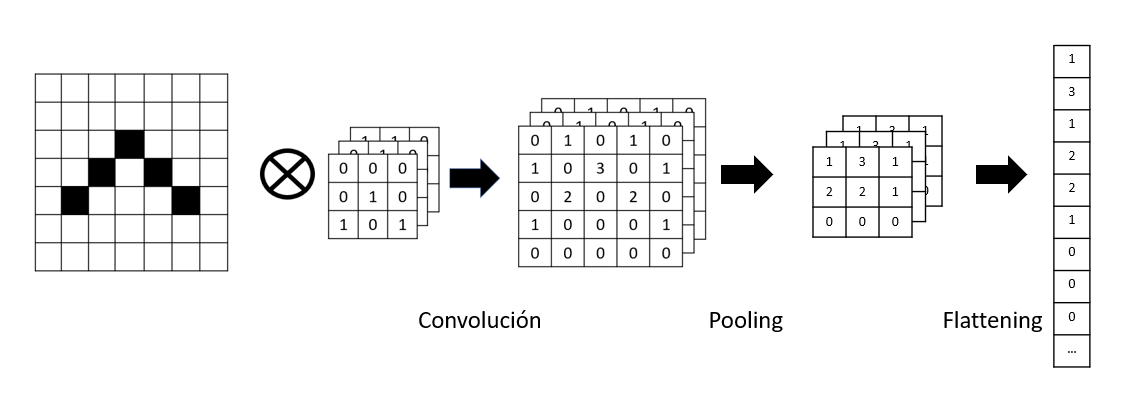
La operación de convolución es una operación habitual en el procesado de imágenes, bien para detectar ciertos patrones en ellas o para transformar las imágenes en sí. Lo que hace esta operación es aplicar una matriz de tamaño N x N, llamada matriz de convolución, sobre la imagen. Por ejemplo, imaginemos que tenemos una imagen binaria con ceros (blanco) y unos (negro), representando un dibujo.

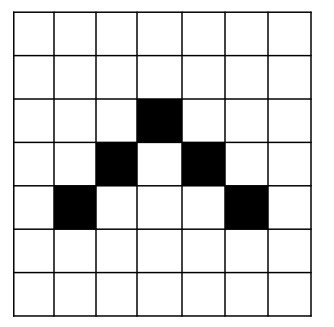
Podríamos definir una matriz de convolución de 3 x 3 con la siguiente información, y aplicarla por la imagen.

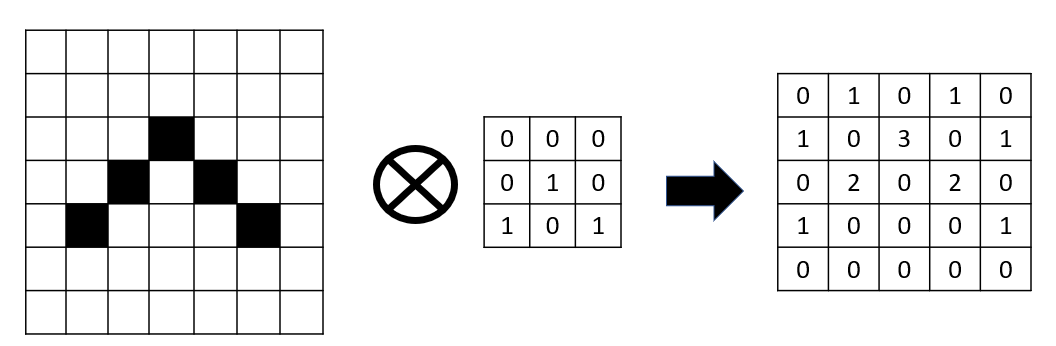
Lo que hacemos es sobreponer la malla de 3 x 3 en cada zona de la imagen, y obtener como resultado la suma de los productos en cada casilla.

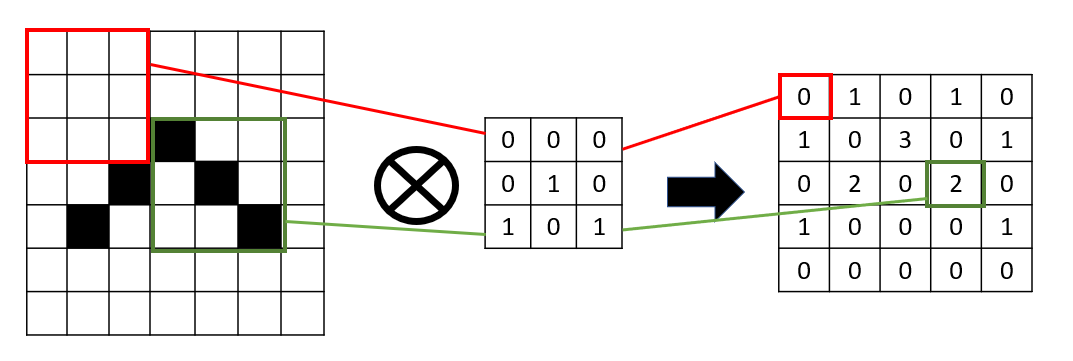
Notar que así obtenemos una imagen resultado algo inferior (pasamos de una imagen de 7 x 7 a un resultado de 5 x 5), donde se ha identificado un patrón en la imagen. En este caso, hemos identificado esquinas superiores (casilla con un "3" en el resultado).

Podemos repetir este proceso aplicando distintas matrices de convolución, de forma que cada una detecte un rasgo de la imagen que nos resulte relevante (esquinas, bordes, etc.)

Ejemplos de convoluciones con GIMP

GIMP es un editor de imágenes gratuito, con unas funcionalidades similares a Photoshop en cuanto a edición y retoque de imágenes. Ofrece la posibilidad de aplicar matrices de convolución sobre las imágenes, para resaltar u obtener determinadas características. Por ejemplo, imaginemos una imagen como ésta de la catedral de Santa Maria del Fiore, en Florencia.

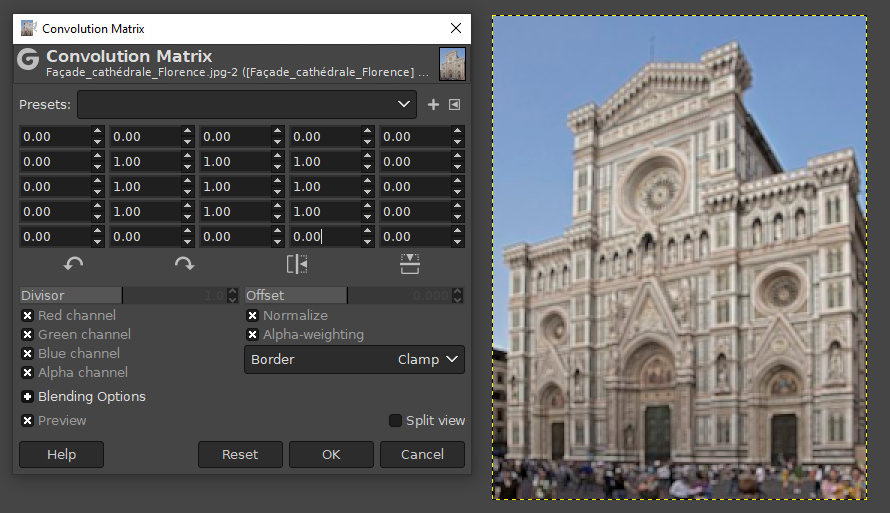
si aplicamos una matriz como la siguiente (menú Filters > Generic > Convolution Matrix en GIMP), obtendremos un resaltado de los bordes (sharpening), ya que estamos resaltando el color de cada píxel respecto a los 4 que le rodean.

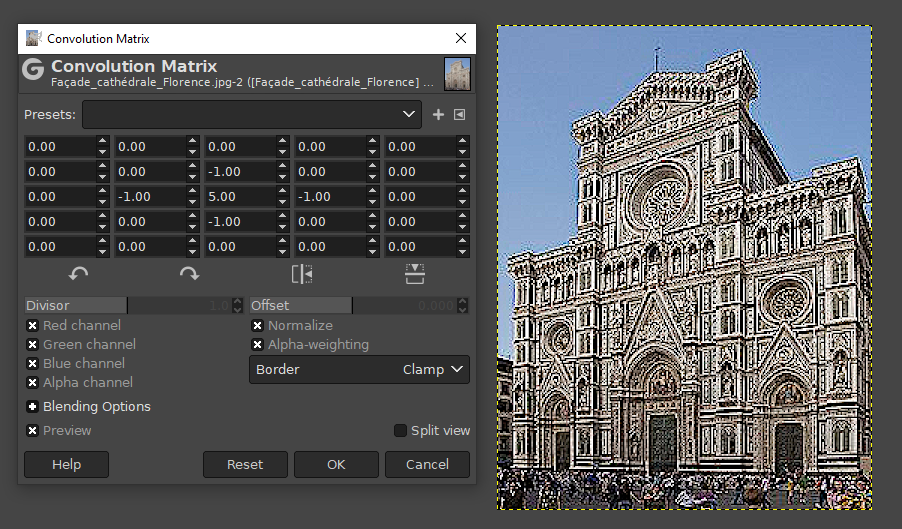
Esta otra matriz hace un difuminado (blur), mezclando el color de un píxel con el de los píxeles circundantes:

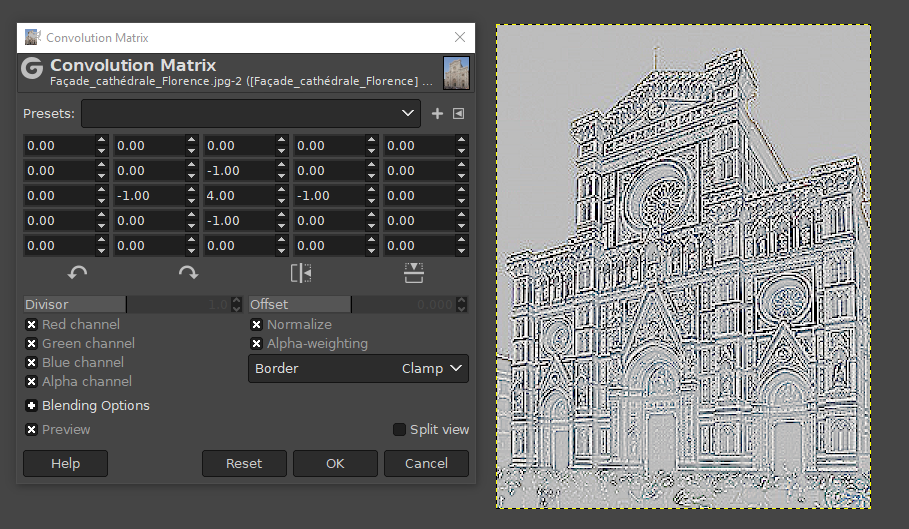
Esta otra matriz detecta los bordes de la imagen, anulando (dejando a 0) los píxeles que sean similares a sus circundantes

1.1.1. Sobre la matriz de convolución¶

En los ejemplos anteriores hemos visto una matriz de convolución de tamaño 3x3 o 5x5, respectivamente. Generalmente el tamaño de filas y columnas suele ser un número impar, para poder tener un elemento "central" en la matriz. Además, cuanto mayor sea el tamaño de la matriz de convolución, más se reducirá el tamaño de la imagen original al aplicar la operación. Así, al aplicar una matriz de 3x3 reduciremos 2 píxeles de ancho y 2 de alto, pero al aplicar una matriz de 5x5 reduciremos 4 píxeles de ancho y 4 de alto. Hay que notar que esto nos hará perder información de la imagen original pero, a cambio, nos centraremos en identificar las características relevantes.

En el caso de no querer perder resolución, lo que se suele hacer es definir un borde negro del mismo grosor que los píxeles que se van a perder. De este modo, se puede aplicar también la matriz en los píxeles de los bordes, sin perder información final.

1.1.2. Convolución y ReLU¶

Es habitual encontrar una operación de ReLU (Rectificador Lineal Unitario) después de una operación de convolución. Recordemos, según se explicó en otro documento que estas funciones ponen a 0 los valores que no lleguen a un cierto umbral, y mantiene con su valor los que sí llegan a ese umbral. ¿Qué utilidad puede tener una función ReLU en una operación de convolución? Nos va a servir para homogeneizar a nulo (cero) todos los valores que la convolución no haya resaltado. Esto permitirá resaltar mejor las formas o los patrones de la imagen sobre el resto de píxeles.

1.2. El subsampling o pooling¶

El subsampling es un paso crucial en las redes convolucionales, ya que permite simplificar una región de una imagen. Se divide la imagen convolucionada en recuadros de tamaño N x N, y de cada recuadro se toma un único valor. Existen principalmente dos técnicas para ello:

Max-Pooling, que consistiría en reemplazar los datos de la rejilla por el máximo valor obtenido en ella
Average Pooling, que consistiría en reemplazar los datos de la rejilla por su media

Así funcionaría en el caso de un max-pooling de 2 x 2:

La utilidad de este paso es doble:

Por un lado, se reduce el tamaño de los datos a analizar. De cada x valores seleccionaremos uno. Cuanto mayor sea el tamaño de la ventana de pooling, más se reducirán los datos. Por tanto, conviene elegir un tamaño adecuado para no simplificar demasiado la información: cuanto mayor tamaño tenga la ventana, más información se perderá, pero más se simplificarán los datos para las capas sucesivas.
Por otro lado, se independiza más la imagen del elemento que se quiere identificar. Si queremos identificar semáforos, por ejemplo, es posible que estos aparezcan verticales, inclinados, distorsionados... De lo que se trata es de identificar los rasgos característicos del semáforo (marcados con valores altos en la etapa de convolución) junto con algunas características generales que suelen rodearles. Así, el resultado de una operación de pooling contendrá los elementos significativos de cada zona de la imagen, resumidos.

1.3. Convoluciones jerarquizadas¶

Las operaciones de convolución y pooling pueden aplicarse secuencialmente sobre una imagen.

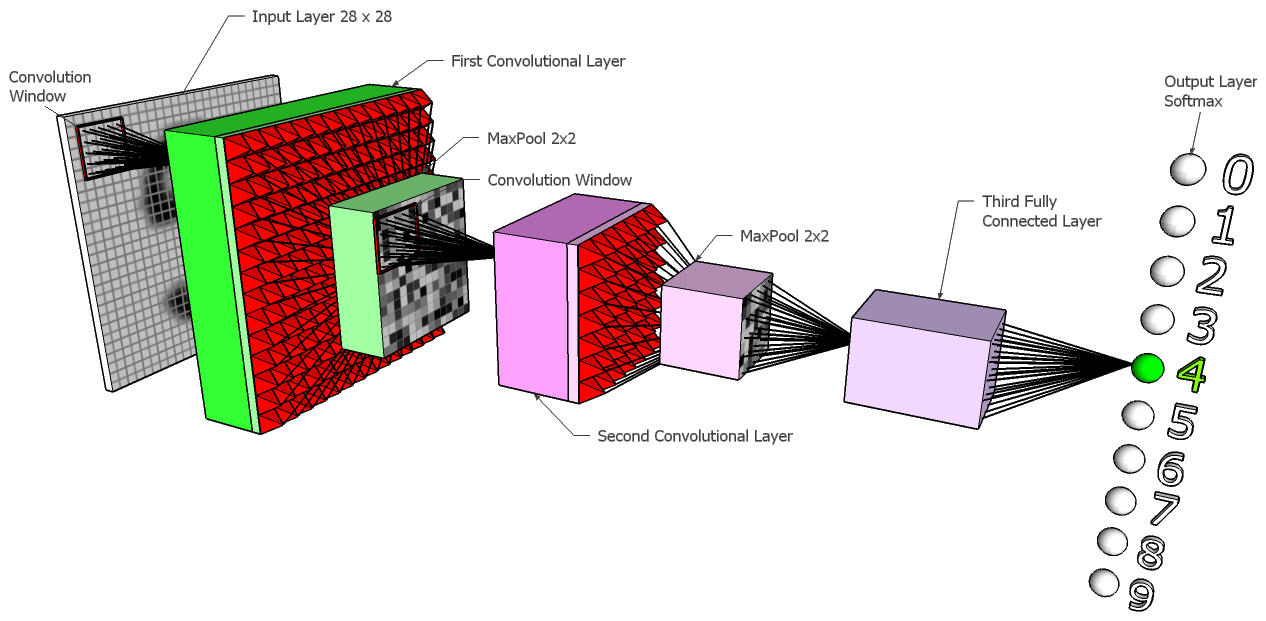
En las primeras capas los filtros solo se aplican sobre una pequeña parte de la imagen, pero después de varias operaciones de subsampling los filtros aplicados pueden ver toda la imagen. Esto crea una jerarquía de características en la que en las primeras capas se aprenden filtros de más bajo nivel (bordes, colores, gradientes, etc.) y progresivamente se van combinando y aprendiendo características de más alto nivel (formas, texturas...). Las características extraídas en las últimas capas de convolución han sido depuradas hasta llegar a una serie de características únicas que permitan discriminar la clase de la que se trata la imagen de entrada.

1.4. El aplanado o flattening¶

Después de las sucesivas operaciones de convolución y pooling que hagamos sobre la imagen original, tendremos como resultado una secuencia de matrices bidimensionales con características extraídas de la imagen. El siguiente paso va a ser convertir cada una de esas matrices en un vector unidimensional con sus valores, y enlazarlos todos en un único (gran) vector unidimensional, resultado de recopilar todas las características relevantes de la imagen de entrada.

1.5. Las capas fully connected¶

Una vez tenemos los datos aplanados, el último paso es pasar esos datos como entrada a lo que sería una red neuronal convencional completamente conectada, con su capa de entrada, su(s) capa(s) oculta(s) y su capa de salida para el resultado final. Observemos que, de este modo, todos los pasos previos de convolución, pooling y flattening que hemos hecho nos han servido para extraer automáticamente las características de la imagen y crear con ellas un vector unidimensional de datos con la información. A partir de este punto, ese vector unidimensional de datos es como cualquier otro que hayamos podido usar en sesiones anteriores con perceptrones multicapa, y podemos emplearlo en una red neuronal convencional. Las neuronas intermedias se activarán o no en función de las características que se detecten de unas u otras categorías.

Aquí podéis ver un ejemplo visual de cómo funcionan las convoluciones y operaciones de pooling sucesivas. Es una web para reconocer y analizar dígitos manuscritos. Escribimos un dígito en el panel superior izquierdo, y se muestran las operaciones de convolución y pooling sucesivas para obtener la capa aplanada (flatten) de información con la que pasar a las capas finales fully connected e identificar el dígito.

1.6. La salida y el error cometido¶

A la hora de emitir un resultado, la RNC normalmente emitirá una probabilidad de que la imagen corresponda a una categoría determinada. Así, en base a distintas categorías, la RNC indicará cuáles de ellas son las más probables para la imagen suministrada. Esto lo conseguiremos definiendo una función de activación softmax, cuya utilidad ya explicamos anteriormente en este documento. Esta función de activación va a ajustar las probabilidades de las neuronas de salida de modo que todas sumen 1, siendo el valor más alto la categoría más probable.

En algunos casos podría interesar proporcionar probabilidades combinadas. Por ejemplo, si estamos reconociendo objetos en imágenes y una imagen tiene más de un objeto, será de esperar que haya más de una probabilidad alta en el resultado (al menos una por cada objeto identificado). En este caso la función de activación softmax no nos servirá, porque no queremos distinguir entre una cosa u otra, sino que puede haber varias. Será necesario definir otra función de activación, como por ejemplo la sigmoidea y normalizar los resultados finales de otro modo para que la suma no sea necesariamente 1.

En cuanto a la medida del error, a pesar de que podemos utilizar funciones de coste fáciles de entender como el error cuadrático medio (MSE), es habitual que en redes convolucionales se utilice la función de entropía cruzada (cross entropy), que marca mucho más la diferencia de errores cometidos en este tipo de redes. Esto será válido, evidentemente, siempre que usemos la red para una tarea de clasificación, y no de regresión. En este último caso será más aconsejable una función de coste como MAE (error absoluto medio) o MSE (error cuadrático medio).

En este vídeo tienes una explicación de los fundamentos de redes convolucionales que hemos visto hasta ahora. También aquí, correspondiente al canal Dot CSV. Es importante tener clara esta base antes de ponernos a programar.

2. Redes convolucionales con Keras/TensorFlow¶

Para definir redes convolucionales con Keras/TensorFlow utilizaremos algunas clases ya empleadas en documentos anteriores, como la clase keras.models.Sequential para definir la secuencia de capas, o keras.layers.Dense para definir las capas fully connected de la fase final del proceso. Pero, además, es necesario hablar de otras etapas y capas nuevas en este proceso.

2.1. Procesamiento de las imágenes de entrada¶

Para poder procesar las imágenes de entrada como datos de entrenamiento usaremos el método image_dataset_from_directory del paquete keras.utils (documentación aquí). Este método acepta, entre otros, los siguientes parámetros:

La carpeta de donde tomar las imágenes (en una ruta absoluta o relativa a la carpeta actual)
labels: indica qué etiquetas se deben tomar para clasificar las imágenes de entrada. Un valor muy habitual es inferred, para que se deduzcan de las subcarpetas existentes dentro de la carpeta principal indicada en el parámetro anterior.
label_mode: indica el modo de etiquetado que se aplicará. Algunos valores habituales son binary (para clasificadores binarios medidos con entropía cruzada binaria), categorical (para clasificadores categóricos medidos con entropía cruzada categórica), o int (para otras clasificaciones medidas con otras métricas).
class_names: sólo en el caso de que el parámetro labels sea inferred, podemos indicar aquí en forma de lista los valores de las categorías que queremos identificar (y que deben coincidir con los nombres de las subcarpetas existentes).
color_mode: puede tomar los valores grayscale, rgb (valor por defecto) o rgba
batch_size: tamaño de los paquetes de imágenes que se formarán para pasarlos al modelo. Por defecto es 32
image_size: tupla indicando el tamaño de las imágenes de entrada (altura y anchura, en ese orden)

Aquí vemos un ejemplo donde indicamos que las imágenes de entrenamiento están en una subcarpeta train en la carpeta actual. Las queremos proporcionar con un tamaño de 128x128, y dentro de esa carpeta hay dos subcarpetas con las categorías perros y gatos (clasificación binaria). La carpeta test tiene una distribución similar para el test:

from keras.utils import image_dataset_from_directory

...

train_dataset = image_dataset_from_directory(
    '.\\train',
    image_size=(128, 128),
    labels='inferred',
    label_mode='binary',
    class_names=['perros', 'gatos']
)

test_dataset = image_dataset_from_directory(
    '.\\test',
    image_size=(128, 128),
    labels='inferred',
    label_mode='binary',
    class_names=['perros', 'gatos']
)

2.1.1. Escalado de valores y data augmentation¶

Además, resulta conveniente normalizar los valores de la imagen en una escala de 0 a 1. Para ello podemos emplear la clase Rescaling del paquete keras.layers:

from keras.layers import Rescaling

...

normalizar = Rescaling(1./255)

Por otra parte, la técnica del data augmentation permite generar múltiples datos a partir de uno en particular. En este caso, a partir de una imagen podemos generar otra similares volteando la imagen, rotándola, ampliándola... Para lograr este proceso podemos emplear las clases RandomFlip, RandomRotation, RandomZoom y/o RandomTranslation del paquete keras.layers:

from keras.layers import RandomFlip, RandomRotation, RandomZoom, RandomTranslation

...

data_augmentation = Sequential([
    RandomFlip("horizontal"),       # Volteo horizontal
    RandomRotation(0.2),            # Rotaciones de hasta el 20% de 360º
    RandomZoom(0.1),                # Zoom de hasta el 10% (hacia dentro/fuera)
    RandomTranslation(0.1, 0.1)     # Desplazamiento vertical y horizontal
])

Podemos aplicar estas dos cosas al conjunto de entrenamiento, y sólo el escalado al de test (ya que en este caso no se necesita generar nuevas imágenes para entrenamiento):

train_dataset = train_dataset.map(lambda x, y: (data_augmentation(normalization(x)), y))
test_dataset = test_dataset.map(lambda x, y: (normalization(x), y))

Note

El parámetro y en las operaciones lambda anteriores representa la etiqueta asignada a cada imagen que, en estos casos, no se altera (sólo se altera la imagen en sí).

2.2. Construcción de la red¶

Además de las capas Input y Dense, para construir una red convolucional vamos a necesitar también otras capas especiales, disponibles en el paquete keras.layers:

Por un lado, usaremos Conv2D, que nos permitirá añadir capas convolucionales a la red.
Además, para aplicar el pooling y reducir el tamaño de las convoluciones emplearemos MaxPooling2D.
Finalmente, para el aplanado que dará paso a las capas fully connected usaremos una capa especial llamada Flatten.

Así, tras el procesado de imágenes visto en el paso previo, podríamos construir una red convolucional de este modo:

from keras.models import Sequential
from keras.layers import Input, Dense, Conv2D, MaxPooling2D, Flatten

...

modelo = Sequential()

# Suponemos imágenes a color de 128 de alto por 128 de ancho (en ese orden)
# Debe coincidir con el tamaño del preprocesamiento anterior
modelo.add(Input((128, 128, 3)))

modelo.add(Conv2D(filters=32, kernel_size=(3, 3), activation='relu'))
modelo.add(MaxPooling2D(pool_size=(2, 2)))

modelo.add(Conv2D(filters=64, kernel_size=(3, 3), activation='relu'))
modelo.add(MaxPooling2D(pool_size=(2, 2)))

modelo.add(Flatten())

Hemos creado una red con dos capas convolucionales (con sus correspondientes pooling posteriores). Algunos aspectos relevantes a comentar:

En las capas Conv2D especificamos el número de filtros distintos de convolución que se aplicarán (y que se generan aleatoriamente, según el tamaño de kernel indicado). Normalmente las capas de convolución tienen una función de activación relu para desactivar las neuronas que no detecten ninguna característica relevante.
En las capas MaxPooling2D definimos el tamaño de la matriz de pooling (2x2, en este caso)

El número de filtros por capa es totalmente experimental. Podemos probar con 32 y 32, o 32 y 64, o añadir más capas... hasta que encontremos resultados satisfactorios. Notar también que es habitual definir pocos filtros en las primeras capas (donde el tamaño de las imágenes aún puede ser grande) y aumentarlo en capas posteriores, donde ya se han reducido con operaciones de pooling.

2.2.1. Las capas fully connected¶

Llegamos al paso final de la RNC, donde creamos las capas finales totalmente conectadas, que leerán la información del vector aplanado de la etapa anterior y emitirán un resultado (típicamente una clasificación de la imagen o una identificación de elementos). Emplearemos para ello la clase keras.layers.Dense que ya hemos utilizado para redes neuronales artificiales en anteriores documentos.

La primera capa que añadamos tomará las conexiones de la capa Flatten anterior. Dependiendo del tamaño final de esa capa deberemos darle un tamaño intermedio adecuado. Podemos probar con tamaños de 100-150 (previendo un vector de características relativamente grande), y luego irlo variando para ver cómo obtenemos mejores resultados.

Podemos añadir tantas capas intermedias como queramos, y finalizar con una capa de salida que tendrá tantas neuronas como elementos queramos clasificar:

Si sólo queremos distinguir entre dos elementos, podemos colocar una única neurona de salida con activación sigmoide. La función de coste, si es un problema de clasificación, podría ser la entropía cruzada binaria (binary_crossentropy).
Si queremos distinguir entre más categorías, añadiremos una neurona por cada categoría, con activación softmax. En este caso, la función de coste al compilar la red será la entropía cruzada categórica (categorical_crossentropy).

Este ejemplo nos serviría para una capa intermedia de 128 neuronas, con una capa de salida de una neurona y activación sigmoide.

modelo.add(Dense(128, activation='relu'))
modelo.add(Dense(1, activation='sigmoid'))

2.3. Compilación y entrenamiento¶

Ahora vamos a compilar nuestro modelo con algún optimizador (por ejemplo, adam) y la función de pérdida que hemos indicado anteriormente (entropía cruzada binaria, ya que sólo queremos distinguir en este ejemplo entre dos categorías de imágenes).

modelo.compile(optimizer='adam', loss='binary_crossentropy', 
    metrics=['accuracy'])

Lanzamos luego el entrenamiento con fit, indicando en los parámetros el generador que hemos configurado antes para las imágenes de entrenamiento y test.

modelo.fit(train_dataset, validation_data=test_dataset, epochs=25)

Note

El proceso de entrenamiento en redes con imágenes suele ser bastante más largo que en redes neuronales tradicionales. Recuerda también que puedes utilizar Google Colab para entrenar tu red convolucional, incluso coger las imágenes de tu cuenta de Google Drive. Aquí se explica cómo.

Ejercicio 1

Utiliza este conjunto de imágenes para crear una RNC que aprenda a distinguir entre personas con mascarilla y sin mascarilla (2 categorías). Guarda el modelo entrenado en un archivo.

2.4. Predicción de nuevos datos de entrada¶

Una vez tenemos una red neuronal convolucional entrenada con resultados satisfactorios, podemos usarla con nuevas imágenes de entrada. Podemos ubicar estas imágenes en una carpeta determinada (por ejemplo, una carpeta datos en la carpeta de trabajo actual) y pasarlas al modelo para que diga su predicción. En este punto nos pueden resultar de utilidad las funciones load_img y img_to_array del paquete keras.preprocessing.image, junto con la función convert_to_tensor de tensorflow para convertir los arrays de pixels de la imagen en tensores aptos como entrada de TensorFlow.

Veamos un ejemplo completo suponiendo que tenemos las imágenes en una subcarpeta datos de nuestra carpeta actual:

import os
import keras
import tensorflow
from keras.preprocessing.image import load_img, img_to_array

... # Cargamos el modelo

imagenes = []
nombres_imagenes = []

for nombre_archivo in os.listdir('.\\datos'):
    ruta_imagen = os.path.join('.\\datos', nombre_archivo)
    if ruta_imagen.endswith(('.jpg', '.jpeg', '.png')):
        # Redimensionamos al tamaño de entrada del modelo
        img = load_img(ruta_imagen, target_size=(128, 128))
        img_array = img_to_array(img)
        # Escalamos valores
        img_array = img_array / 255.0
        imagenes.append(img_array)
        nombres_imagenes.append(nombre_archivo)

# Convertir la lista de imágenes a un tensor
imagenes_tensor = tensorflow.convert_to_tensor(imagenes)

# Evaluar cada imagen
predicciones = modelo.predict(imagenes_tensor).flatten()
clases_predichas = (predicciones >= 0.5).astype(int)

Como puede verse en el ejemplo, recorremos todas las imágenes válidas de la carpeta de entrada, las redimensionamos y escalamos, y añadimos el array de valores escalados por un lado y el nombre del fichero por otro, en dos listas paralelas. Finalmente convertimos a tensores las imágenes y las pasamos al método predict del modelo para obtener las predicciones. Hay que tener en cuenta que, aunque sea un clasificador binario, las predicciones de cada modelo se devuelven en forma de lista (de un solo elemento, con la probabilidad asignada), por eso llamamos al método flatten para dejar los valores fuera de las sublistas.

Ejercicio 2

Utiliza el modelo entrenado del ejercicio anterior para que catalogue estas imágenes que le proporcionaremos. Las guardaremos en una subcarpeta prueba dentro de la carpeta de trabajo, y el programa deberá decir por pantalla a qué categoría pertenece cada imagen. En este caso, como es una clasificación binaria, tendremos un valor entre 0 y 1, y dependiendo de lo cerca que esté del 0 o del 1 se asociará a una categoría u otra.

Ejercicio 3

Utiliza este conjunto de imágenes para crear una RNC que aprenda a distinguir entre distintos tipos de comidas. En este caso se proporcionan varias categorías de comida, y clasificadas tanto en la carpeta de entrenamiento como en la de test. Prueba después a pasar una imagen externa de alguna de las categorías estudiadas para ver qué resultado predice. Puedes usar estas imágenes de ejemplo

3. Transfer learning aplicado a redes convolucionales¶

El transfer learning (que podríamos traducir por "aprendizaje por transferencia" en castellano) es una estrategia que permite utilizar conocimientos ya adquiridos para resolver unos problemas, y aplicarlos para resolver otros problemas diferentes. Por ejemplo, si una persona sabe tocar la guitarra y quiere aprender a tocar el piano, no tiene que volver a empezar su aprendizaje desde cero: puede retomar sus conocimientos sobre teoría musical (notas musicales, partituras, temporización...) y aplicarlos en la práctica del piano.

Aplicado al mundo del deep learning, básicamente consiste en utilizar modelos ya creados para resolver ciertas tareas, desacoplar ciertas capas y añadir una nueva parte de red neuronal que nos ayude a resolver otras tareas diferentes. Por ejemplo, un modelo entrenado para reconocer ciertos tipos de imágenes puede adaptarse fácilmente para reconocer otros tipos.

3.1. Tipos de transfer learning¶

Podemos aplicar transfer learning de varias formas:

Inductive transfer learning, o "aprendizaje por transferencia inductivo". En la transferencia inductiva, los datos de origen y de destino son diferentes, pero pertenecen al mismo dominio o tienen características similares. En este caso, tanto el conjunto de datos de origen como el de destino tienen etiquetas y la idea es utilizar el conocimiento adquirido en la tarea de origen para mejorar el rendimiento en la tarea de destino. Por ejemplo, dado un modelo que identifique distintos tipos de flores, podemos usarlo para identificar rosas.
Unsupervised transfer learning, o "aprendizaje por transferencia no supervisado". En la transferencia no supervisada, los datos de origen y de destino no tienen etiquetas. El objetivo de la transferencia no supervisada es encontrar patrones o características comunes en ambos conjuntos de datos, sin la necesidad de tener etiquetas. Se suele utilizar para la reducción de dimensionalidad o el agrupamiento de datos en diferentes categorías.
Transductive transfer learning, o "aprendizaje por transferencia transductivo". En la transferencia transductiva, la tarea de origen y la tarea de destino son la misma tarea, pero los dominios son diferentes. En este caso, los datos de origen se utilizan para ajustar el modelo a la distribución de los datos de destino, que pueden ser diferentes. La transferencia transductiva se utiliza comúnmente en la clasificación de texto o en la traducción de idiomas, donde la tarea es la misma, pero los dominios pueden ser diferentes. Por ejemplo, un sistema de procesamiento del lenguaje basado en noticias de diarios online, podría entrenarse también a través de mensajes en Twitter u otras redes sociales.

En resumen, la transferencia inductiva se utiliza cuando los datos de origen y destino son diferentes, pero pertenecen al mismo dominio, la transferencia no supervisada se utiliza cuando los datos de origen y destino no tienen etiquetas, y la transferencia transductiva se utiliza cuando la tarea es la misma, pero los dominios son diferentes.

3.2. Estrategias para transfer learning¶

Normalmente a la hora de trabajar con transfer learning se parte de un modelo pre-entrenado de alto rendimiento, desarrollado sobre grandes cantidades de datos de entrada. Sobre esta base, se pueden aplicar dos estrategias principales:

Extraer características. En modelos profundos se suele alcanzar un alto grado de detección de características. Ocurre, por ejemplo, con las redes convolucionales; las últimas capas convolucionales disponen de información de muchos detalles extraídos de las imágenes de entrada, que se pasan a las capas fully connected del final para emitir un resultado. La idea sería utilizar esta misma red quitando la capa final. De este modo la red se comporta como un extractor de características fijas.
Ajuste de modelos. Es un proceso similar al anterior (partimos de un modelo avanzado y pre-entrenado) donde, además de quitar la última capa, podemos re-entrenar selectivamente otras capas para un nuevo propósito. Así, dejamos una serie de capas fijas e inmutables, y otras entrenan y adaptan sus pesos para una nueva tarea. De este modo acortamos el tiempo de entrenamiento (hay capas ya entrenadas) y podemos obtener mejores resultados.

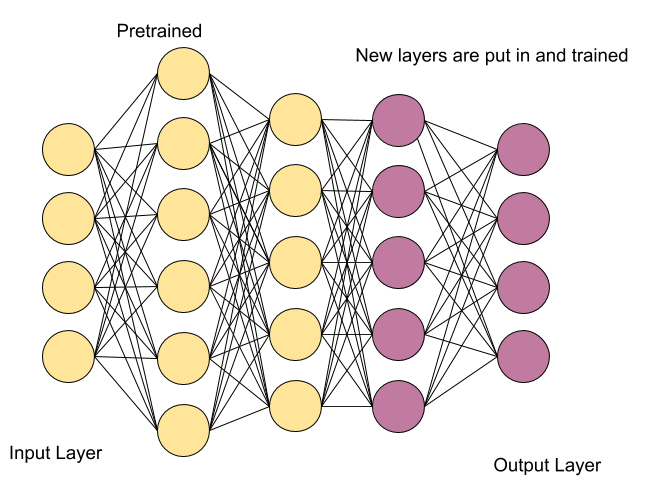
3.3. Ejemplo: clasificación de imágenes¶

Vamos a adaptar mediante transfer learning un modelo pre-entrenado de MobileNet que distingue hasta 1.000 categorías de imágenes distintas. Lo que haremos será utilizar directamente el modelo para que catalogue un conjunto de imágenes, viendo los errores que comete. Después desacoplaremos la capa fully connected del final para añadir otra propia, que entrenaremos específicamente para el nuevo objetivo, viendo cómo se mejoran los resultados.

Usaremos estas imágenes de comidas para ver cómo las cataloga el modelo pre-entrenado. Construimos un pequeño programa que cargue el modelo y procese una a una las imágenes:

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
import tensorflow_hub as hub
import PIL.Image as Image
import tf_keras

# Parte 1: probamos a identificar unas imágenes

url_modelo1 = 'https://www.kaggle.com/models/google/mobilenet-v2/TensorFlow2/035-224-classification/2'
tam_imagenes = (224, 224)
imagenes = ['imagen_prueba_donut.jpg', 'imagen_prueba_guacamole.jpg',
            'imagen_prueba_nachos.jpg']

modelo1 = tf_keras.Sequential([
    hub.KerasLayer(url_modelo1, input_shape = tam_imagenes + (3,))
])

for fichero_imagen in imagenes:
    imagen = Image.open(fichero_imagen).resize(tam_imagenes)
    imagen = np.array(imagen) / 255
    resultado = modelo1.predict(imagen[np.newaxis, ...])
    codigo = np.argmax(resultado[0])
    fichero_etiquetas = tf.keras.utils.get_file('ImageNetLabels.txt',
        'https://storage.googleapis.com/download.tensorflow.org/data/ImageNetLabels.txt')
    etiquetas = np.array(open(fichero_etiquetas).read().splitlines())
    print(fichero_imagen, ":", etiquetas[codigo])

Si ejecutamos el ejemplo, podemos ver que la clasificación es aproximada, pero no del todo correcta. El donut lo cataloga como bagel (panecillo redondo de forma similar a un donut), y los nachos también los cataloga como guacamole.

Ahora utilizaremos el mismo modelo de una forma diferente: en lugar de cargar todo el modelo cargaremos las capas convolucionales que sirven como extractor de características. Después le acoplaremos una red fully connected al final y entrenaremos sólo esta última parte de la red, dejando fijo el resto. Así, el entrenamiento será más rápido, y la complejidad del modelo pre-entrenado que usamos hará que la identificación de las imágenes sea mejor. Para el entrenamiento usaremos este conjunto de imágenes que ya hemos utilizado en un ejercicio anterior, con multitud de imágenes de las tres categorías que nos interesan (donuts, nachos y guacamole).

Por lo tanto, el primer paso será cargar una URL de modelo alternativa, donde sólo seleccionamos la parte del extractor de características. Lo marcamos como no entrenable, para que no se reajusten los pesos que ya tiene ajustados:

# Parte 2: transfer learning
url_modelo2 = 'https://www.kaggle.com/models/google/mobilenet-v2/TensorFlow2/tf2-preview-feature-vector/4'
extractor = hub.KerasLayer(url_modelo2, input_shape = tam_imagenes + (3,))
extractor.trainable = False

Ahora construimos un nuevo modelo donde la primera parte será este extractor de características, y la última una capa fully connected que sí entrenaremos:

modelo2 = tf.keras.Sequential(
    extractor,
    # Crearemos una red para identificar 3 tipos de comida
    tf.keras.layers.Dense(3, activation='softmax')
)
modelo2.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

A continuación, definimos los generadores de imágenes sobre el conjunto de entrenamiento anterior, para que aprenda a predecir las tres categorías o clases que hemos indicado, en el orden en que queramos:

clases = ['donuts', 'guacamole', 'nachos']
batch_size = 32
carpeta_train = '.\\imagenes_comidas\\train'
carpeta_test = '.\\imagenes_comidas\\test'
imagenes_train = 800 * 3
imagenes_test = 200 * 3

gen_imagenes_train = ImageDataGenerator(rescale = 1./255,
                            shear_range = 0.2,
                            zoom_range = 0.2,
                            horizontal_flip = True)
gen_imagenes_test = ImageDataGenerator(rescale = 1./255)

datos_train = gen_imagenes_train.flow_from_directory(\
    directory = carpeta_train,
    target_size=tam_imagenes, color_mode='rgb', 
    classes=clases, 
    class_mode='categorical')

datos_test = gen_imagenes_test.flow_from_directory(\
    directory = carpeta_test,
    target_size=tam_imagenes, color_mode='rgb', 
    classes=clases,     
    class_mode='categorical')

Finalmente, entrenamos el modelo usando estos generadores:

modelo2.fit(datos_train, steps_per_epoch=imagenes_train//batch_size,
    epochs=5, validation_data=datos_test,
    validation_steps=imagenes_test//batch_size)

Tras el entrenamiento, podemos volver a pasar las imágenes de prueba a la red para que prediga los resultados:

for fichero_imagen in imagenes:
    imagen = Image.open(fichero_imagen).resize(tam_imagenes)
    imagen = np.array(imagen) / 255
    resultado = modelo2.predict(imagen[np.newaxis, ...])
    codigo = np.argmax(resultado[0])
    print(fichero_imagen, ":", clases[codigo])

Podemos comprobar cómo ahora la clasificación final de las imágenes de prueba es correcta, y se ajusta a las categorías que nosotros hemos establecido. La duración del entrenamiento, ante una misma complejidad de modelo, también será más corta, porque sólo se reajustan los pesos de las capas finales fully connected. En este caso no se aprecia mucha diferencia porque la complejidad del modelo MobileNet es mayor que la de la red convolucional que hicimos anteriormente, y el proceso de calcular productos por pesos, convoluciones, poolings, etc, es más costoso en esta red. Sin embargo, con menos cantidad de epochs se alcanzan resultados muy satisfactorios.