El muestreo de Thompson¶
En este documento vamos a abordar uno de los algoritmos de aprendizaje por refuerzo que podemos aplicar en estrategias de inteligencia artificial, conocido como muestreo de Thompson (Thompson sampling). Su principal área de aplicación son juegos o programas en los que se quiera buscar el máximo beneficio a partir de ciertos datos en principio aleatorios o desconocidos. Al entrar en juego la aleatoriedad o el desconocimiento de los datos de entrada, hay que recalcar que se trata de un modelo estocástico, donde podremos obtener resultados diferentes cada vez que lo ejecutemos.
1. Un ejemplo introductorio¶
Para ilustrar el funcionamiento de este algoritmo, supongamos que queremos jugar una cantidad de dinero (por ejemplo, 1000 euros) en un conjunto de N máquinas (por ejemplo, N=5). Cada máquina acepta un euro y, aleatoriamente, devuelve el doble del dinero introducido. Es decir, podemos perder el euro que hemos echado o ganar un euro extra. Cada máquina tiene una probabilidad fija de dar premio, pero nosotros no la conocemos. El problema a resolver es... ¿cómo podemos maximizar la cantidad de dinero que ganamos jugando los 1000 euros que tenemos?
1.1. Preparando el problema¶
Vamos a preparar los datos iniciales del problema para resolverlo después en Python. Necesitamos disponer de las probabilidades aleatorias de las N = 5 máquinas: números al azar entre 0 y 1. También almacenamos la cantidad total de dinero a gastar.
import numpy as np
N = 5
dinero = 1000
probabilidades = np.random.rand(N)
1.2. Primer planteamiento¶
Un primer planteamiento puede consistir en jugar 100 euros en cada máquina (500 en total) y, dependiendo de la que nos haya dado más premios, jugar los 500 euros restantes en esa máquina. Esto conformaría nuestro algoritmo para el proceso de decisión (tercer principio de la IA comentado en documentos anteriores).
Vamos con la primera parte: crearemos un array donde almacenaremos los aciertos obtenidos en cada una de las N máquinas (inicializado con ceros). Después, formamos un bucle anidado donde, para cada máquina, jugamos 100 euros consecutivamente en ella y vamos incrementando los aciertos que tengamos.
# Inicializamos un array con N ceros (aciertos en cada máquina)
aciertos = np.zeros(N)
# Bucle para jugar 100 euros en cada máquina e incrementar el contador
# correspondiente
for i in range(N):
for n in range(100):
# Generamos un número aleatorio
aleatorio = np.random.rand()
# Si es menor que la probabilidad de la máquina, contamos un acierto
if aleatorio <= probabilidades[i]:
aciertos[i] += 1
Notar que, para ver si hemos ganado o no, generamos un número aleatorio entre 0 y 1. Si no supera la probabilidad de la máquina en cuestión, es un acierto.
Ahora vamos con la segunda parte: seleccionaremos la máquina que tenga más aciertos (usaremos para ello una función llamada argmax de NumPy, que obtiene el índice con el mayor valor), y jugaremos los 500 euros restantes en esa máquina, incrementando los aciertos que tengamos.
# Nos quedamos con la máquina con más aciertos
maximo = aciertos.argmax()
print("La mejor máquina es:", maximo + 1)
# Jugamos el resto del dinero (500 euros) en esa máquina
for i in range(500):
aleatorio = np.random.rand()
if aleatorio <= probabilidades[maximo]:
aciertos[maximo] += 1
Finalmente, para saber qué beneficios hemos tenido basta con sumar cuántos aciertos ha habido en el array aciertos (tanto en la máquina seleccionada como en el resto de máquinas, usadas durante la primera parte de la prueba).
print(f"Hemos ganado {aciertos.sum()} euros")
2. Fundamentos del muestreo de Thompson¶
La estrategia anterior puede ser buena, pero no es la mejor. Quizá haber jugado 100 euros en cada máquina es excesivo, y nos ha hecho perder mucho dinero que podríamos haber invertido antes en la mejor máquina. O quizá no ha sido suficiente, y hemos elegido una máquina que no es la mejor en cuanto a probabilidad. El muestreo de Thompson es un algoritmo que adapta su decisión en cada iteración, evaluando cuál es la mejor máquina en cada momento.
Para ello, el algoritmo toma una función de distribución (explicaremos este concepto a continuación) llamada β(a,b), que recibe dos parámetros. Simplificaremos la explicación diciendo que cuanto mayor sea el primer parámetro, mejor es la solución elegida, y cuanto mayor sea el segundo parámetro, peor es la solución elegida.
2.1. Funciones de distribución. La función beta¶
Una función de distribución es una función que determina, para un determinado valor, la probabilidad de que una variable tenga dicho valor. Normalmente se representa en una gráfica bidimensional. En el eje X (horizontal) representamos todos los posibles valores que la variable puede tomar, y en el eje Y (vertical) representamos la probabilidad que tiene cada valor, o el número de veces que se ha dado respecto al total estudiado.
Por ejemplo, este gráfico muestra un rango de salarios en el eje X, y la probabilidad de que una persona tenga uno de esos salarios en el eje Y (fuente: diario El País, año 2017, a través de datos del INE).
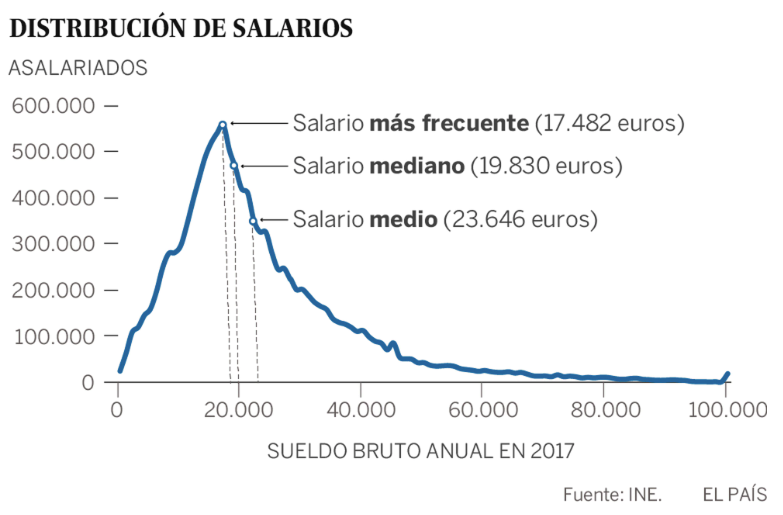
Atendiendo a esta distribución, lo más probable es que, si elegimos una persona al azar de la muestra, esa persona tenga un salario cercano a los 17.482 euros, en este caso. Es poco probable, por ejemplo, que esa persona gane 60.000 euros anuales, según este gráfico de distribución.
En cuanto a las distribuciones beta, no vamos a entrar en su definición completa matemática, que puede ser difícil de digerir. Pero, en pocas palabras, ayudan a determinar cuál es el valor más probable que puede tomar una variable dados los parámetros a y b que la regulan. En el caso que nos ocupa de las N máquinas, cada máquina tiene su propia distribución beta, que indica cuál es el valor más probable o, dicho de otro modo, con qué probabilidad podemos obtener éxito.
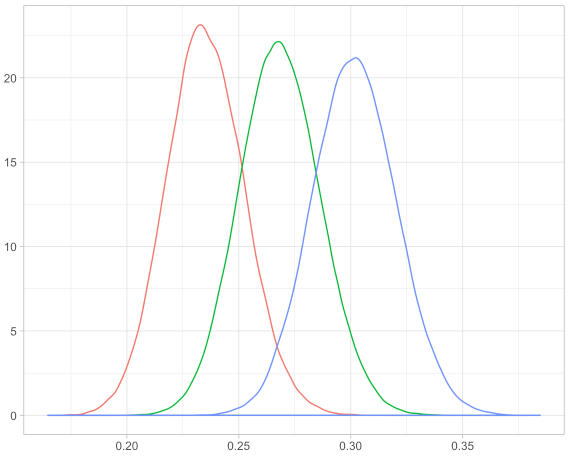
En la gráfica anterior, la máquina representada por la gráfica azul tiene mayor probabilidad de éxito que las otras, ya que su distribución queda más a la derecha (probabilidad cercana a 0.30). Esta distribución se calcula en base a los parámetros a y b que recibe la distribución. Cuanto mayor sea el primero, mejor será la solución que estamos examinando, y cuanto mayor sea el segundo, peor será esa solución. Parece lógico pensar, aplicado a nuestro problema, que el primer parámetro esté asociado al número de aciertos en una máquina i, y el segundo al número de fallos en esa máquina i. Cuantos más aciertos tenga una máquina, mejor será elegirla, y cuantos más fallos hayamos tenido con ella, menos la elegiremos.
2.2. Implementando el segundo planteamiento¶
Por ello, vamos a definir dos arrays: uno para contar los aciertos de cada máquina y otro para los fallos. Los inicializamos ambos a cero. También podemos definir un tercer array para ver cuántas veces se selecciona cada máquina, y así sacar al final estas estadísticas.
aciertos = np.zeros(N)
fallos = np.zeros(N)
seleccionadas = np.zeros(N)
Ahora vamos con nuestro proceso de decisión: recorreremos todo nuestro dinero (es decir, iremos euro a euro) y, en cada iteración, evaluaremos con la función β cuál de las N máquinas tiene mejor valor. Esta función β está incorporada en NumPy, dentro del mismo objeto random que hemos usado para generar datos aleatorios. Le pasaremos como primer parámetro (a) el número de aciertos de cada máquina en ese momento, y como segundo parámetro (b) el número de fallos. La llamada a la función np.random.beta nos dará un valor de lo buena o mala que es esa máquina en cuestión. En realidad, obtiene un valor al azar de la distribución beta que le digamos, con lo que, cuanto más "a la derecha" esté la distribución, mejor valor obtendremos (recuerda el gráfico anterior).
Recorriendo todas las máquinas, veremos cuál es la mejor. Este código podría quedar algo así:
# Bucle para jugar todo el dinero
# En cada iteración, con la función beta elegimos la mejor opción en cada momento
for i in range(dinero):
# Elegimos la máquina en base a la función beta
mejor = 0
elegida = 0
for j in range(N):
beta = np.random.beta(aciertos[j] + 1, fallos[j] + 1)
if beta > mejor:
mejor = beta
elegida = j
# Ya hemos seleccionado una máquina para esta iteración
seleccionadas[elegida] += 1
# ... Falta terminar este bucle
Nota
Como puedes ver, sumamos 1 a cada parámetro a y b porque la definición de la función beta no permite valores de 0 o negativos. En cualquier caso, todas las máquinas parten con una misma configuración inicial de a = 1, b = 1, y luego va variando para cada una, en función de los aciertos y fallos que genere.
¿Cómo terminamos lo que queda de bucle? Una vez hemos elegido la mejor máquina (variable elegida), generamos un número aleatorio como antes y, si no supera la probabilidad de esa máquina, contamos un acierto. Si lo supera, contamos un fallo.
# Vemos si ganamos o no con esa máquina, y actualizamos aciertos/fallos
# Generamos un número aleatorio
aleatorio = np.random.rand()
# Si es menor que la probabilidad de la máquina, contamos un acierto
if aleatorio <= probabilidades[elegida]:
aciertos[elegida] += 1
else:
fallos[elegida] += 1
Finalmente, sólo queda sumar los aciertos para ver cuánto hemos ganado, como en el primer planteamiento. Podemos mostrar también cuántas veces se ha elegido cada máquina con este método.
print(f"Hemos ganado {aciertos.sum()} euros")
for i in range(N):
print(f"La máquina {i+1} ha sido seleccionada {seleccionadas[i]} veces")
2.3. Conclusiones¶
Podemos comprobar el funcionamiento de todo este proceso, y contrastar la primera y segunda estrategias planteadas, a través de este ejemplo hecho en Google Colab.
En este caso, haber gastado 100 euros en cada máquina es, en general, excesivo, y nos hace perder más dinero de la cuenta. Podemos ver cómo con la segunda estrategia las máquinas con peor probabilidad se descartan rápidamente y apenas acumulan intentos. Quizá durante las primeras jugadas haya dudas, y el algoritmo no tenga muy claro cuál es la que tiene mayor probabilidad, y nos haga elegir diferentes máquinas. Pero en poco tiempo los datos convergen y se estabilizan. De este modo nos aseguramos de que elegiremos la mejor máquina tan pronto como la detectemos.
Si recordamos de un documento anterior, en todo problema de inteligencia artificial se tienen una serie de principios básicos: entradas/salidas, recompensa, proceso de decisión y feedback o recompensa. Aplicados a este problema en cuestión:
- La entrada sería la ronda en la que estamos (número de iteración) y el número de aciertos y fallos acumulados de las máquinas hasta ese momento
- La salida sería la máquina que elegimos en la iteración actual (analizando la entrada con la función beta)
- La recompensa o feedback está clara: obtendremos +1 euro si acertamos, y -1 si fallamos (incrementamos aciertos o fallos, respectivamente)
- El proceso de decisión es el bucle for en su conjunto, que analiza la entrada, toma una decisión, recoge el resultado y actualiza los datos de aciertos/fallos
2.4. Entendiendo mejor la función "beta"¶
Imaginemos que una máquina tiene una probabilidad de dar premio del 80% (aunque eso de entrada nosotros no lo sabemos). Durante las primeras 10 pruebas en esa máquina , es posible que su parámetro a sea cercano a 8 y su parámetro b sea cercano a 2. Al cabo de 100 pruebas la proporción no cambiaría: el parámetro a estará cercano a 80 y el b a 20. Y al cabo de 1000 pruebas en esa máquina a estará cercano a 800 y b a 200. En principio, todos estos valores son equivalentes, pero la función de distribución que se dibuja es distinta.
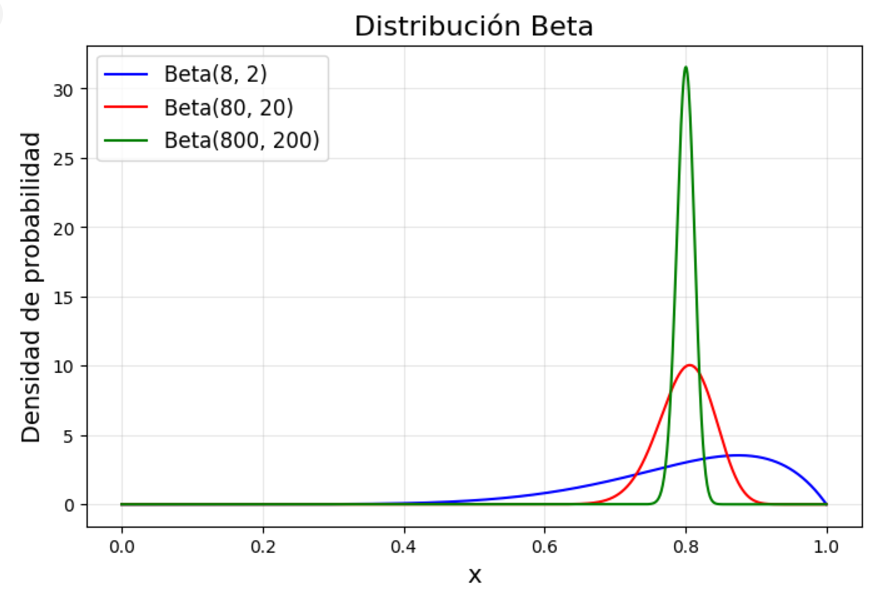
En el caso de pocas pruebas (beta(8, 2), curva azul) el pico de la gráfica está cerca de 0.8 (aunque no coincide), pero la curva es muy ancha, lo que indica que esa probabilidad aún no es muy cierta, y puede variar a los lados. Obtener un valor aleatorio de esa función de distribución puede dar valores muy dispares, entre 0.4 y 1 aproximadamente.
En cambio, al cabo de 100 iteraciones (beta(80, 20), curva roja) la curva se estrecha y se centra más en 0.8. Obtener un valor aleatorio de esa distribución ya acota más el resultado entre 0.7 y 0.9 aproximadamente, con predominio en la zona alrededor de 0.8
Tras 1000 iteraciones (beta(800, 200), curva verde), el estrechamiento es aún más pronunciado en torno a 0.8, ya se tiene mucha más certeza de que la probabilidad es ésa, y el valor al azar tomado estaría en torno a 0.75 - 0.85 aproximadamente.
Ejercicio 1
Vamos a poner en práctica el muestreo de Thompson con este otro supuesto práctico:
Una empresa de comercio electrónico tiene una serie de clientes registrados. Quiere intentar captar a cuantos pueda para ofrecerles un nuevo plan Premium en el que, por una pequeña cantidad anual, podrán gozar de mayores ventajas que el resto.
Para ello, la empresa dispone de 7 diferentes estrategias publicitarias. Unas son más discretas y las otras más "agresivas", en cuanto a lo que se muestra en la página. La empresa no tiene muy claro cuál de estas estrategias va a resultar más adecuada para captar a la mayor cantidad posible de clientes para su plan Premium.
El objetivo no es para tomarlo a la ligera, ya que la empresa tiene un millón de clientes. Suponiendo que el plan Premium cueste 30 euros al año, una estrategia publicitaria que sólo capte al 1% de clientes le reportaría 10.000 x 30 = 300.000 euros. En cambio, si la estrategia consigue captar al 10% de clientes, los beneficios ascenderían a 3.000.000 euros.
Nuestra tarea es determinar cuál de las estrategias tiene más aceptación entre los clientes en el menor tiempo posible. Para ello, tomaremos una muestra de 10.000 clientes y mostraremos a cada cliente una de las estrategias, e iremos viendo si se une al plan o no, de forma que poco a poco iremos descartando las estrategias que menos captan, y quedándonos con la(s) que más.
Deberemos determinar:
- Las entradas al sistema
- La salida
- La recompensa o feedback
- El proceso de decisión
- Finalmente, determinaremos cuál es la estrategia seleccionada y qué porcentaje de los clientes que la han visto se ha suscrito al plan Premium
Debemos suponer una tasa de aceptación relativamente baja de, como mucho, el 20%, para no crear grandes expectativas. Es decir, la probabilidad "teórica" de elegir cualquiera de las estrategias publicitarias no debe superar el 20%.
Ejercicio 2
En este documento CSV se dispone de una serie de resultados de partidos entre equipos de la NBA en la temporada 2020-2021, entre los meses de diciembre y febrero. Verás que es un documento CSV con muchas columnas, pero sólo nos interesan cuatro de ellas:
- Visitor, nombre del equipo visitante
- VisitorPTS, puntos anotados por el equipo visitante
- Home, nombre del equipo local
- HomePTS, puntos anotados por el equipo local
Sobre estos datos vamos a aplicar una estrategia basada en el muestreo de Thompson para, dados dos nombres de equipos que se enfrentan en un partido, estimar quién de los dos va a ganar el partido. Para ello, asumiremos que un equipo será mejor cuantos más partidos haya ganado, y peor cuantos más partidos haya perdido. Será también importante distinguir si los partidos los ha ganado como local o como visitante.
El programa leerá los datos del fichero y construirá su esquema de predicción basado en dicho muestreo de Thompson. En este otro archivo se dispone de un fichero de texto predicciones.txt donde se indica primero el nombre del equipo visitante y luego el del local (separados por coma). El programa deberá estimar para cada partido quién será el ganador. En el fichero predicciones_solucion.txt de ese mismo fichero ZIP se tiene el marcador real que tuvieron esos partidos. En base a las predicciones y a los resultados reales saca por pantalla para cada partido si se acertó o no.