El algoritmo MiniMax¶
En este documento vamos a explicar el algoritmo MiniMax, utilizado en teoría de juegos para elegir la mejor opción en determinados juegos, especialmente juegos por turnos de dos jugadores. Veremos que también puede tener otras aplicaciones, más allá del ámbito de los juegos.
1. Fundamentos¶
MiniMax es un algoritmo utilizado para tomar decisiones en teoría de juegos, y encontrar el mejor movimiento para un jugador, asumiendo que su oponente también intenta buscar la mejor jugada para él (y la peor para su oponente). Por lo tanto, como jugadores, debemos tomar nuestra decisión suponiendo que después el oponente va a intentar perjudicarnos lo máximo posible.
Como decíamos, se utiliza en juegos por turnos de dos jugadores, como el 3 en raya, backgammon, ajedrez, etc, aunque también puede tener otras aplicaciones. Para poderlo aplicar, deben cumplirse una serie de premisas:
- Es un método determinista: siempre que lo aplicamos sobre un mismo estado inicial obtenemos el mismo resultado
- Para estrategias de juegos basados en turnos (normalmente de dos jugadores)
- De suma nula, es decir, lo que gana un jugador es lo mismo que lo que pierde el otro.
- Con información perfecta, es decir, los dos jugadores tienen conocimiento completo del estado del juego en todo momento.
El algoritmo se basa en dos elementos:
- Un maximizador, que intenta obtener la puntuación más alta posible en su turno
- Un minimizador, que intenta obtener la puntuación más baja en su turno.
Cada estado del juego tiene un valor asociado. Los valores altos beneficiarán al maximizador, y los valores bajos al minimizador. Si el maximizador tiene ventaja, el valor final tenderá a ser alto, y si no, tenderá a ser bajo.
Por ejemplo, imaginemos un juego ficticio cuyos posibles estados finales tienen las siguientes valoraciones:
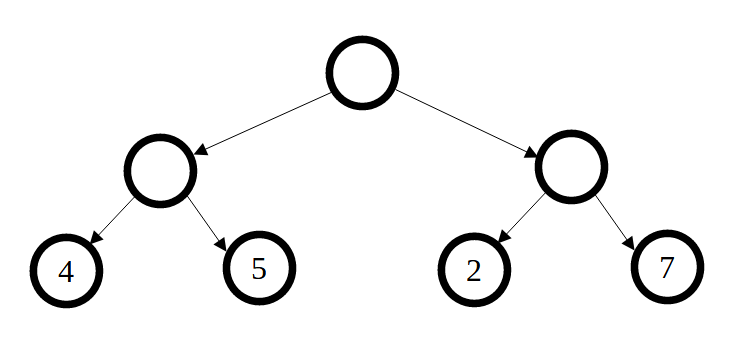
Supongamos que somos el maximizador y nos toca mover. Si elegimos el camino de la derecha para intentar buscar nuestro máximo beneficio (7), luego el minimizador elegirá el subcamino izquierdo para lograr su máxima recompensa (2). En este caso, nos interesará elegir el camino de la izquierda para que el minimizador obtenga un premio menor (4).
Si el juego lo inicia el minimizador, eligiendo el camino derecho para buscar nuestra mejor jugada (2) hará que en el siguiente turno el maximizador elija el subcamino derecho para obtener la suya (7), con lo que saldríamos perdiendo. Será mejor elegir el camino izquierdo para que el maximizador obtenga un premio menor (5).
1.1. Algoritmo general¶
El algoritmo general MiniMax es un algoritmo recursivo donde, a partir de un estado (nodo del árbol de estados), exploramos todas las posibles opciones hasta llegar a los nodos hoja. Dependiendo de si somos maximizador o minimizador, elegiremos la opción que nos convenga. Así quedaría el algoritmo de procesamiento de un nodo N:
funcion MiniMax(N)
{
Si N es nodo hoja, devolver f(N)
Si no:
Generar sucesores de N (N1, N2...)
Evaluar sucesores N1, N2...
Si N es MAX, devolver el máximo de los sucesores
Si N es MIN, devolver el mínimo de los sucesores
}
Hay que tener en cuenta que, en cada nueva llamada recursiva, se invierten los turnos (los nodos hijos de un MAX pasan a ser MIN porque es el turno del oponente, y viceversa).
2. Aplicación: 3 en raya¶
Vamos a poner en práctica este algoritmo jugando al juego del 3 en raya, conocido en inglés como tic-tac-toe. Es un juego con un tablero de 3 x 3 casillas, inicialmente vacías, que dos jugadores van completando por turnos, añadiendo dos tipos de fichas (una para cada jugador). Gana el jugador que consiga formar una fila, columna o diagonal con sus fichas. Si ninguno de los dos lo consigue una vez se llena el tablero, se tiene un empate.
Asumiremos para nuestro juego que el jugador 1 usará como ficha el símbolo de la X mayúscula, y el jugador 2 usará el símbolo de la O mayúscula. Las casillas vacías las representaremos con guiones -. Supondremos que el jugador 1 actúa como maximizador, y el 2 como minimizador. De este modo:
- Aquellos nodos finales u hoja en los que el jugador 1 gane los asociaremos con una puntuación positiva de +1
- Aquellos nodos finales u hoja en los que el jugador 2 gane los asociaremos con una puntuación negativa de -1
- Aquellos nodos finales u hoja donde ninguno gane (empate) los asociaremos con una puntuación de 0
Imaginemos que el tablero se encuentra en esta situación, y le toca elegir al jugador 1 (maximizador, ficha X):
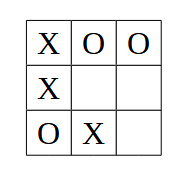
En primer lugar, generaríamos las posibles jugadas del turno del jugador 1:
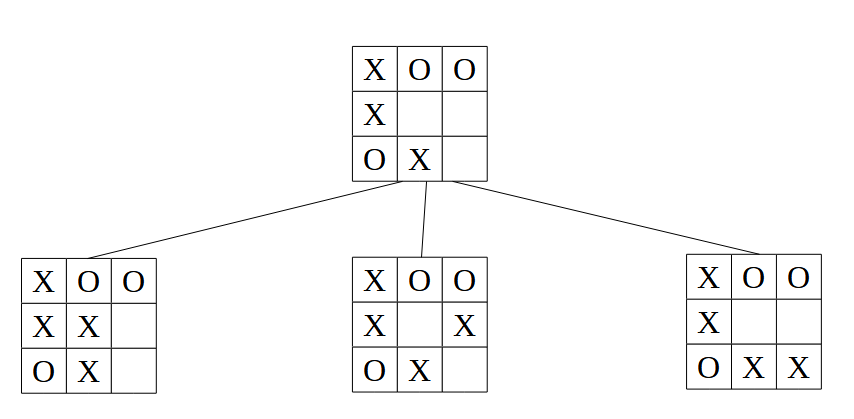
Después, a partir de cada jugada anterior, generamos las dos posibles jugadas del jugador 2:
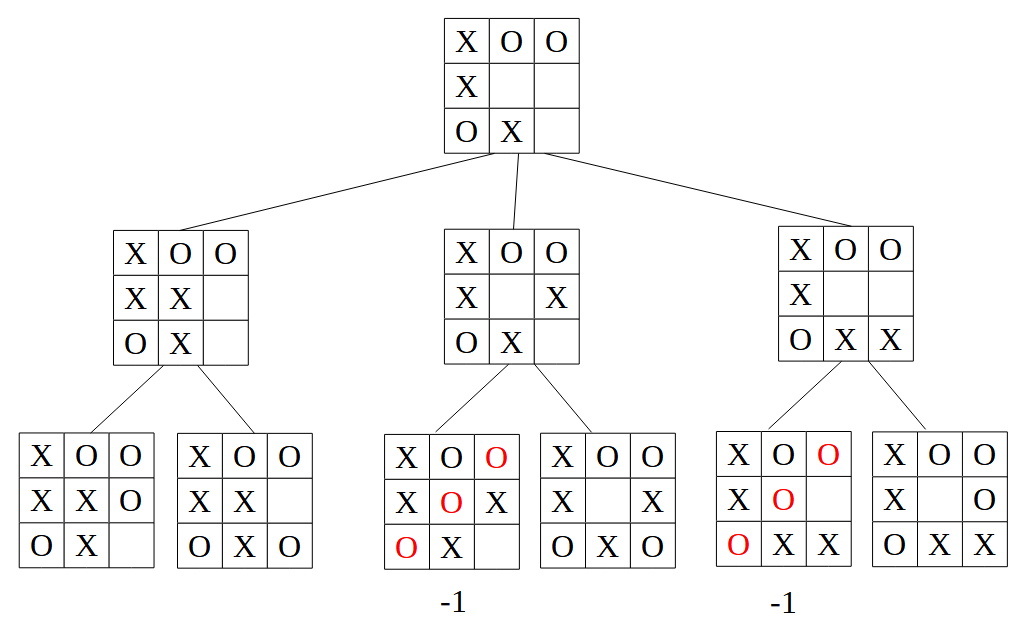
Notar que en este paso ya hay algunas situaciones donde ganaría el jugador 2. Esto serían nodos hoja que ya no hay que seguir explorando. Dejamos marcadas esas jugadas en rojo, con su puntuación asociada (-1, porque gana el jugador 2).
Finalmente, generamos la única posible jugada en el siguiente turno para jugador 1, a partir de cada jugada anterior que aún queda pendiente. Igualmente, marcamos en azul y calificamos con +1 las jugadas donde termine ganando el jugador 1, y en rojo con -1 las que termine ganando jugador 2. Si alguna jugada terminara en empate, la calificaríamos con 0.
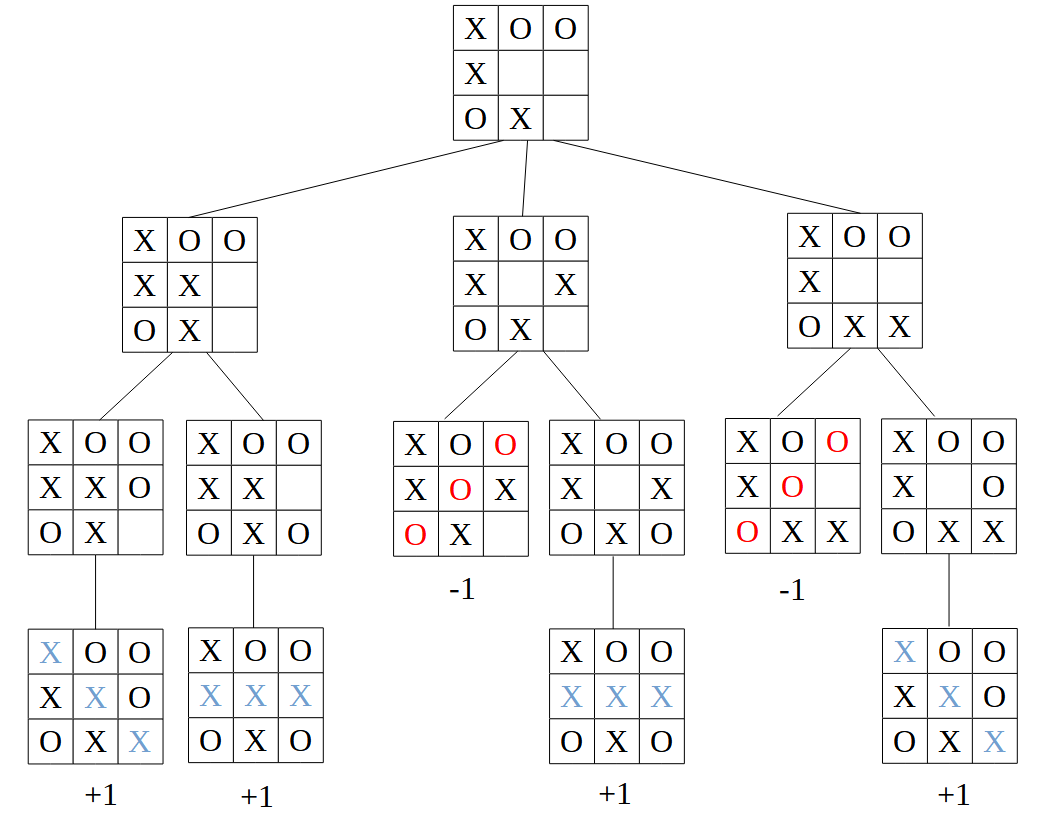
Para decidir qué jugada elegir desde el nodo inicial para el jugador 1, reconstruimos la partida desde los nodos hoja hacia arriba, teniendo en cuenta a quién le tocaría en cada caso. Así, en los niveles donde le toque al jugador 1 elegiremos el nodo con valor máximo, y en los niveles donde le toque al jugador 2 elegiremos los nodos con valor mínimo.
Partiendo desde el nivel inferior, corresponde a jugadas del jugador 1. Como no tiene de dónde elegir (al llegar a ese nivel sólo tiene una posible jugada), simplemente pasamos el valor de cada nodo hoja a su nodo padre:
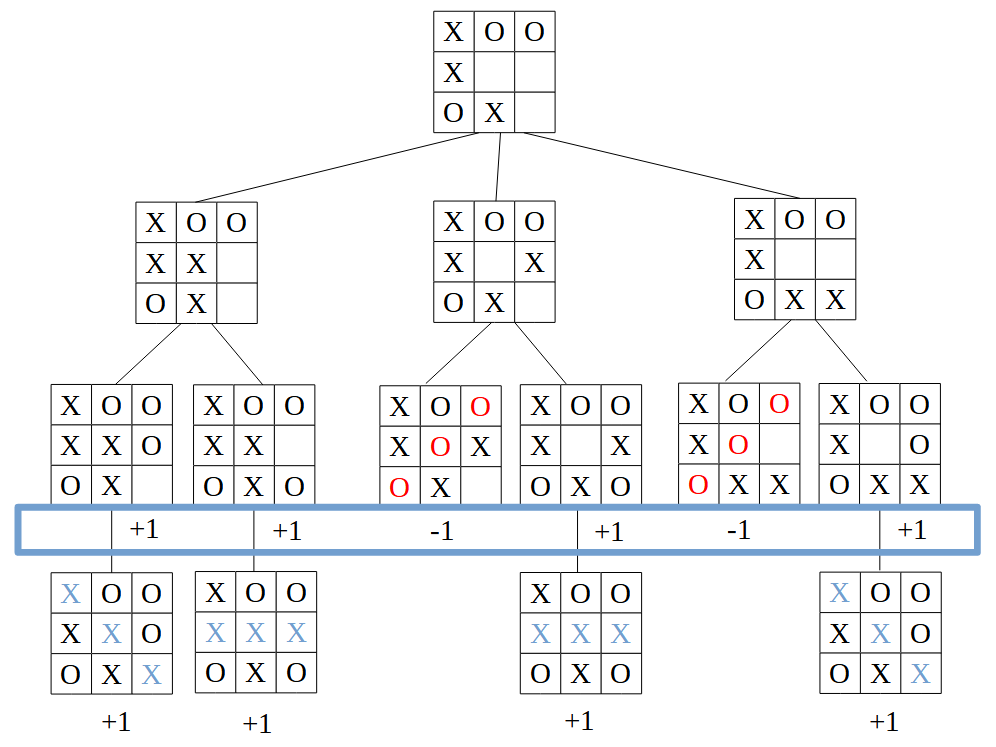
Ahora es el turno del jugador 2 para el siguiente nivel (subimos uno hacia arriba). De cada nodo hijo, elegirá el que tenga el menor valor posible:
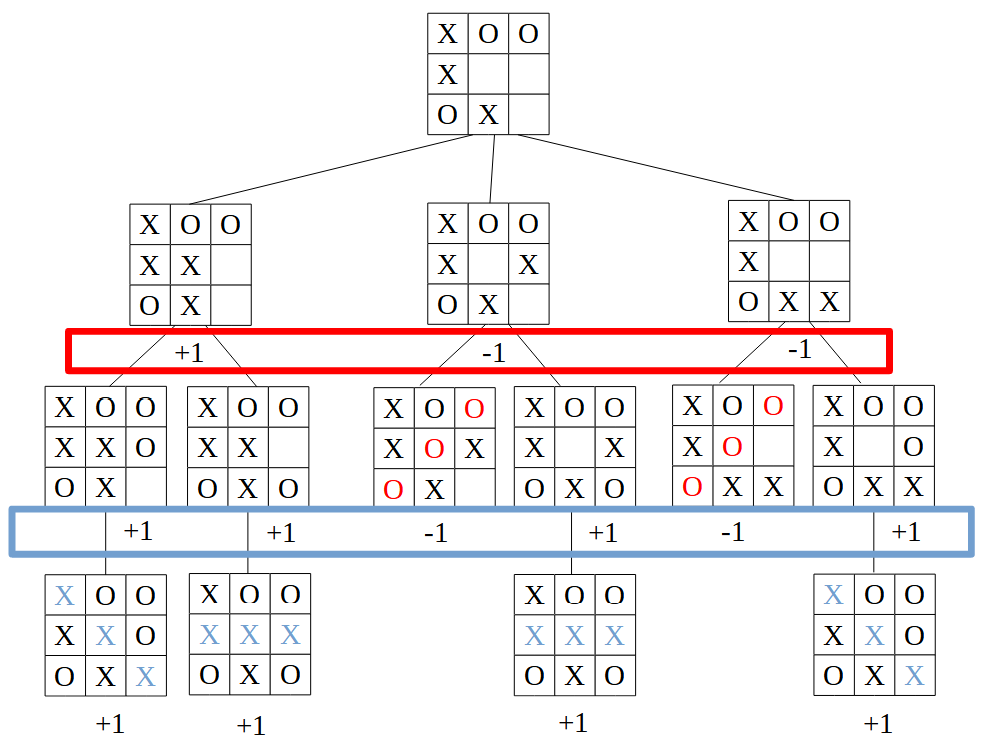
Finalmente, vuelve a ser turno del jugador 1, que buscará el mayor valor entre sus hijos (subimos de nuevo un nivel)
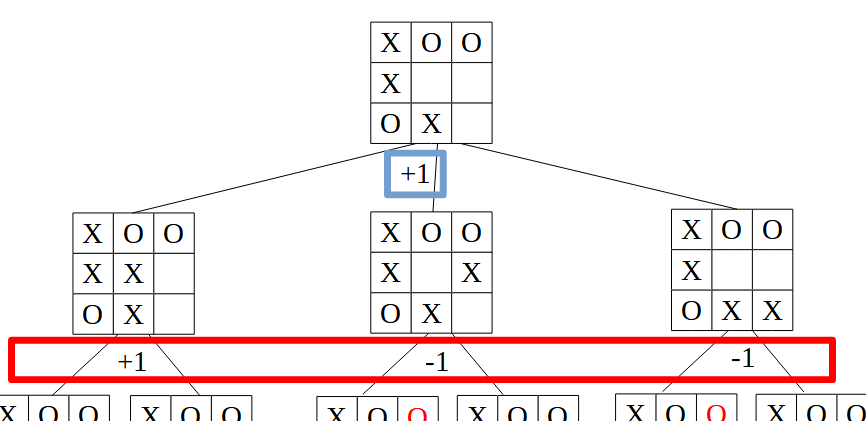
Por lo tanto, el jugador 1 elegirá la jugada de la izquierda, que es la que le garantiza ganar.
2.1. Preparando el entorno del juego¶
Como primer paso, vamos a definir las estructuras de datos que vamos a utilizar para desarrollar el juego. Para definir los tableros de 3 x 3 usaremos NumPy. Partiremos de un tablero con 9 casillas vacías:
import numpy as np
tablero = np.array(['-'] * 9).reshape(3, 3)
Definiremos una función auxiliar imprimirTablero, que reciba un determinado tablero y lo muestre correctamente formateado en pantalla:
def imprimirTablero(tablero):
for i in range(0, tablero.shape[0]):
for j in range(0, tablero.shape[1]):
print(f"|{tablero[i, j]}|", end="")
print()
Definimos también una función generarJugadas, que recibirá como parámetros el tablero actual y a quién le toca jugar (True = jugador 1, False = jugador 2), y generará una lista con todos los posibles siguientes tableros:
def generarJugadas(tablero, turno):
jugadas = []
if turno:
simbolo = 'X'
else:
simbolo = 'O'
for i in range(0, tablero.shape[0]):
for j in range(0, tablero.shape[1]):
if tablero[i, j] == '-':
nuevaJugada = np.array(tablero)
nuevaJugada[i, j] = simbolo
jugadas.append(nuevaJugada)
return jugadas
Observa que lo que hace la función es recorrer las casillas del tablero actual y, cada vez que encuentra un hueco vacío, genera un nuevo tablero a partir del actual y pone una ficha (del jugador correspondiente) en ese hueco. Estos nuevos tableros se agrupan en una lista que se devuelve.
Definimos una función llamada esHoja, que recibe un tablero y determina si es un nodo hoja o no. Devuelve una tupla con un booleano indicando si es hoja (True) o no (False) junto con la valoración del nodo hoja, en caso afirmativo: 1 si gana el jugador 1, -1 si gana el jugador 2, o 0 si es un empate. Si no es un nodo hoja, devolverá 0 como valoración, aunque no se tendrá en cuenta este dato.
def esHoja(tablero):
if any(np.all(tablero[i,:] == 'X') for i in range(3)) or \
any(np.all(tablero[:,i] == 'X') for i in range(3)) or \
np.all(np.diag(tablero) == 'X') or np.all(np.diag(np.fliplr(tablero)) == 'X'):
# Nodo hoja favorable al jugador 1
return True, 1
elif any(np.all(tablero[i,:] == 'O') for i in range(3)) or \
any(np.all(tablero[:,i] == 'O') for i in range(3)) or \
np.all(np.diag(tablero) == 'O') or np.all(np.diag(np.fliplr(tablero)) == 'O'):
# Nodo hoja favorable al jugador 2
return True, -1
elif np.count_nonzero(tablero == '-') == 0:
# Nodo hoja empate
return True, 0
else:
# No es nodo hoja
return False, 0
El grupo if servirá para determinar un nodo hoja en el que gane el jugador 1. El primer elif lo empleamos para determinar un nodo hoja en que gane el jugador 2, y el segundo elif para un nodo hoja con todas las casillas rellenas donde no haya ganado nadie. Finalmente, el else determinará que no se cumple nada de lo anterior y, por tanto, no es un nodo hoja.
2.2. Definiendo el algoritmo¶
Ahora vamos a definir el algoritmo MiniMax que, a partir de un determinado tablero y turno, determine la mejor jugada (bien sea para jugador 1 o 2, según el turno).
def minimax(tablero, turno):
hoja, valor = esHoja(tablero)
resultadoElegido = 0
tableroElegido = np.array([])
if hoja:
return tablero, valor
else:
jugadas = generarJugadas(tablero, turno)
for jugada in jugadas:
tableroJugada, resultadoJugada = minimax(jugada, not turno)
if turno and \
(resultadoJugada > resultadoElegido or len(tableroElegido) == 0):
resultadoElegido = resultadoJugada
tableroElegido = jugada
elif not turno and \
(resultadoJugada < resultadoElegido or len(tableroElegido) == 0):
resultadoElegido = resultadoJugada
tableroElegido = jugada
return tableroElegido, resultadoElegido
Explicamos los pasos que sigue la función:
- Primero comprobamos si el tablero actual es una hoja. Inicializamos las variables
resultadoElegidoytableroElegido, que almacenarán qué jugada se elige en el siguiente turno, y con qué resultado final esperado. - Si el nodo actual es una hoja, devolvemos el tablero tal cual con su valor (ya habríamos terminado)
- Si no es una hoja:
- Generamos todas las posibles jugadas para el turno actual, con el tablero actual
- Recorremos cada posible jugada, y aplicamos recursivamente MiniMax para ese tablero, pasando el turno al otro jugador
- Si es el turno del jugador 1 y el minimax devuelve un resultado mejor que el que tenemos hasta ahora, nos quedamos con ese resultado y la jugada actualmente analizada
- Si es el turno del jugador 2 y el minimax devuelve un resultado peor que el que tenemos hasta ahora, nos quedamos con ese resultado y la jugada actualmente analizada
- Finalmente, devolvemos el resultado mejor para nuestros intereses (después de analizar todas las jugadas), junto con la jugada en sí.
Ejercicio 1
Crea un programa llamado TicTacToe.py y agrupa las piezas que hemos ido poniendo en los ejemplos anteriores. Crea un programa principal que le pida al usuario quién empieza y, en función de eso, cree una partida de 3 en raya donde el jugador 1 será el usuario y el jugador 2 la IA de nuestro programa.
2.3. Descartando jugadas: las podas alpha-beta¶
En el desarrollo del juego, la IA tiene que explorar todas las opciones a partir del tablero actual en busca de una que le haga ganar. Este proceso puede simplificarse descartando opciones que no van a llevar a una solución mejor que una que ya haya encontrado. Es lo que se conoce como podas alpha-beta.
En nuestro caso, cuando estamos evaluando la lista de jugadas, no tiene sentido evaluar más jugadas si ya hemos encontrado una que nos da un resultado ganador (1) para el jugador 1 o perdedor (-1) si le toca al jugador 2. En el primer caso (dejar de explorar cuando encontramos una jugada ganadora para el jugador 1), se le llama poda alpha, y en el segundo (dejar de explorar cuando encontramos una jugada ganadora para el jugador 2) se le llama poda beta.
Nuestra función minimax optimizada podría quedar así:
def minimax_alpha_beta(tablero, turno):
hoja, valor = esHoja(tablero)
resultadoElegido = 0
tableroElegido = np.array([])
if hoja:
return tablero, valor
else:
jugadas = generarJugadas(tablero, turno)
for jugada in jugadas:
tableroJugada, resultadoJugada = minimax_alpha_beta(jugada, not turno)
if turno and \
(resultadoJugada > resultadoElegido or len(tableroElegido) == 0):
resultadoElegido = resultadoJugada
tableroElegido = jugada
if resultadoElegido == 1:
return tableroElegido, resultadoElegido
elif not turno and \
(resultadoJugada < resultadoElegido or len(tableroElegido) == 0):
resultadoElegido = resultadoJugada
tableroElegido = jugada
if resultadoElegido == -1:
return tableroElegido, resultadoElegido
return tableroElegido, resultadoElegido
El único cambio que añadimos es el if interno en cada turno donde, si vemos que la jugada que estamos analizando nos da como ganadores (en uno u otro turno), la devolvemos sin buscar más opciones.
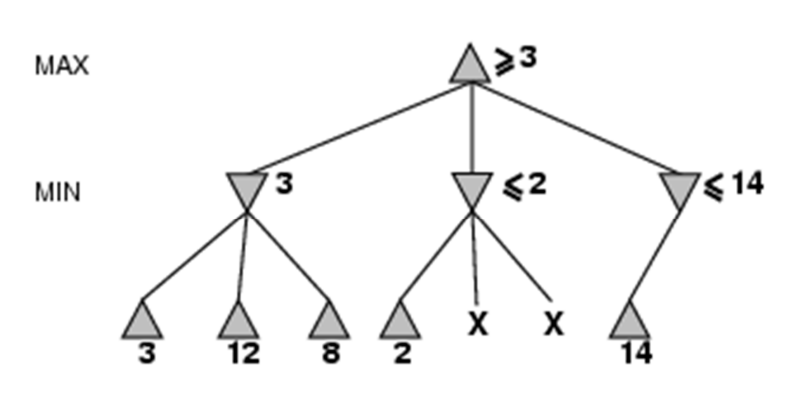
En otros tipos de juegos, la poda es algo más compleja. Por ejemplo, en esta situación hipotética, es turno del maximizador. Expande los nodos y, en el segundo nivel (turno del minimizador), se aplica una poda en el segundo hijo ya que, como el primer resultado es 2, ese nodo va a devolver 2 o menos, y no va a mejorar (para el maximizador) el 3 del primer nodo izquierdo, con lo que el maximizador seguro que no elegirá ese nodo intermedio.
Ejercicio 2
Aplica poda alpha-beta al ejercicio anterior para descartar caminos que no sea necesario explorar. Averigua cuántas llamadas recursivas se harían con la primera versión del programa, y cuántas se hacen con esta poda, para ver lo que supone en términos de eficiencia.
Nota
Puedes ayudarte de variables globales que luego incrementes en cada función con cada llamada. Para usar una variable global desde dentro de una función debes declararla como global en esa función:
variable_global = 0
def funcion():
global variable_global
variable_global += 1
...
3. MiniMax en otros juegos¶
El esquema seguido en el punto anterior para el juego del 3 en raya se puede aplicar de forma similar a otros juegos que cumplan esas características básicas (por turnos de 2 jugadores, de suma nula y con información perfecta). El problema está en que, cuantos más movimientos diferentes, o casillas, tenga el juego, más complejo se vuelve el árbol de posibles jugadas, y en ocasiones puede ser inmanejable construirlo todo (caso del ajedrez). En estos casos, lo que se suele hacer es profundizar desde un estado hasta unos cuantos niveles más y evaluar de algún modo lo buenos o malos que son esos nuevos estados.
Por ejemplo, en el caso del ajedrez, dado un estado del tablero, podemos evaluarlo en base a la puntuación de las fichas de un jugador menos la puntuación de las fichas del otro. Cuanto mayor sea la diferencia, mejor será ese tablero para el jugador 1, y cuanto menor sea, mejor lo será para el jugador 2.
Ejercicio 3
Añadiremos ahora al ejercicio del 3 en raya la opción de que el usuario elija 3 niveles de dificultad:
- Fácil: en este caso, la CPU no usará MiniMax para elegir su jugada, se limitará a rellenar una casilla al azar
- Intermedio: en esta opción, la CPU usará MiniMax al 50%, es decir, en cada turno de la CPU generaremos un número aleatorio entre 0 y 1 y, si es menor de 0.5, usaremos MiniMax para esa jugada, y si no, elegiremos una casilla al azar
- Avanzado: la CPU usará MiniMax en todas las jugadas, como en la solución realizada anteriormente
Ejercicio 4
Vamos a aplicar el algoritmo MiniMax a otro juego por turnos sencillo de implementar: el juego del Nim. Es un juego de 2 jugadores donde se parte con un conjunto de N = 20 fichas en la mesa. Por turnos, cada jugador puede retirar entre 1 y 3 fichas. Pierde el jugador que retira la última ficha.
Elabora un algoritmo MiniMax para que, una vez establecido quién empieza, genere un contrincante inteligente (jugador 2) para un jugador 1 humano.
Solución Ejercicio 4
Aquí puedes ver un vídeo con la solución paso a paso del ejercicio.