Algoritmos genéticos

Los algoritmos genéticos son una rama de lo que se conoce como computación evolutiva, una estrategia de la inteligencia artificial consistente en hacer que el sistema a desarrollar "evolucione" en base a unos parámetros para alcanzar mejores soluciones. Esta computación evolutiva, a su vez, se engloba dentro de la computación basada en modelos naturales que, de algún modo, pretende simular el comportamiento de cierta parte de la naturaleza o del ser humano. Veremos a continuación los principales rasgos de esta estrategia y cómo podemos aplicarla.

1. Fundamentos de los algoritmos genéticos

Los algoritmos genéticos son una estrategia de inteligencia artificial que se aplica en problemas donde queremos que el sistema "aprenda a hacer" algo, y no tenemos muy claro cómo enseñarle. Lo que haremos, como veremos, será imitar el comportamiento de selección natural que existe para los seres vivos, mediante el cual crearemos diferentes versiones del programa e iremos evolucionando y cambiando las mejor preparadas, y descartando las que no obtienen buenos resultados, hasta alcanzar un resultado satisfactorio.

1.1. Conceptos clave

A la hora de trabajar con algoritmos genéticos necesitamos manejar unos conceptos asociados a esta estrategia.

• Partiremos del concepto de individuo: cada una de las instancias del problema que queremos resolver. El conjunto de individuos conformará la población de nuestro algoritmo, del mismo modo que un conjunto de leones conforma la población de una manada en África.
• Cada una de las características relevantes de un individuo se denomina alelo, y juntas constituyen el genotipo de ese individuo. Entendemos por características relevantes, en nuestro caso, aquellas que nos interesa desarrollar para resolver el problema en cuestión.
• Un individuo será "mejor" o "peor" candidato para nuestro problema cuanto mejor sea su genotipo para el objetivo que perseguimos. La ideoneidad de un genotipo la evaluaremos con una función llamada fenotipo o fitness.
• Los individuos de una población pueden iniciar un proceso de reproducción entre ellos, mediante el cual se conforman nuevos individuos. En este proceso de reproducción se da una operación de cruce en la que el nuevo individuo toma ciertas características de uno de sus progenitores y otras características del otro. Por ejemplo, de un padre rubio de ojos marrones y una madre castaña de ojos azules puede salir una niña rubia de ojos azules.
• Algunos individuos también pueden sufrir mutaciones, es decir, alteraciones aleatorias de ciertas características, que no estaban presentes en sus progenitores y que, a partir de ese punto, se pueden transmitir a la futura descendencia de ese individuo. Por ejemplo, altas capacidades intelectuales, lunares o manchas de nacimiento, etc.
• En un momento determinado, la descendencia producida generará un reemplazo de la población anterior, del mismo modo que los individuos de mayor edad dejan tarde o temprano paso a los jóvenes en el mundo natural.
• En todo este proceso, existe una selección de los individuos que mejor se adaptan al entorno en el que viven. Aquellos que no logran adaptarse por alguna característica (debilidad, enfermedad, no descendencia...) desaparecen del proceso evolutivo.

Como vemos, son todo conceptos que se aplican en el mundo natural, a la hora de estudiar la evolución de las distintas especies animales y vegetales. Y son conceptos que asimilaremos también al mundo computacional, para desarrollar nuestros programas.

El esquema (simplificado) que se sigue en el mundo natural, y que intentaremos aplicar en nuestros programas, es el siguiente:

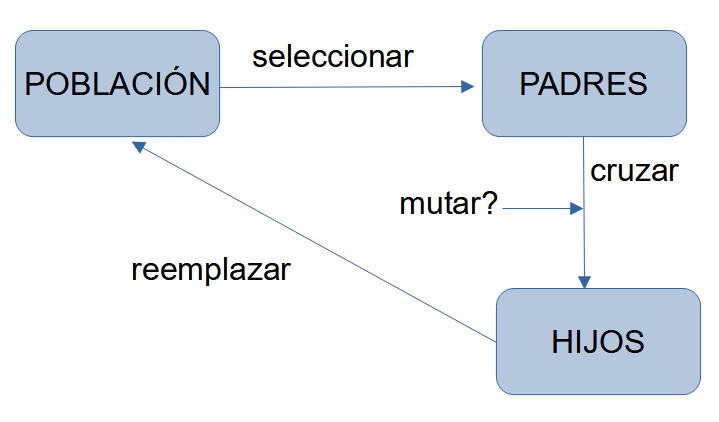
1.2. Proceso general

El proceso general que vamos a seguir es iterativo, a través de un número t de repeticiones, que dependerá de lo que tardemos en alcanzar resultados satisfactorios. Lo podemos describir con los siguientes pasos:

1. Inicializamos t = 0
2. Inicializamos una población inicial de individuos P(t=0). Normalmente, de forma aleatoria.
3. Mientras no se cumpla una condición de parada
4. Evaluar P(t)
5. t = t + 1
6. Seleccionar P(t) desde P(t-1)
7. Cruzar P(t)
8. Mutar aleatoriamente algún(os) individuo(s) del cruce
9. Reemplazar población

Generalmente, el proceso de selección determinará los K individuos mejor preparados (con mejor fenotipo o fitness) de la población, y las operaciones de cruce y mutación se harán sobre esa selección, reemplazando a los individuos menos preparados del conjunto.

Como vemos, el paso 3 es el que define el bucle general que vamos a seguir. Existen dos formas de afrontar los pasos 3, 4 y 6 dentro de ese bucle.

• Estrategias generacionales: durante cada iteración se crea una población completa de nuevos individuos (pasos 3 y 4) que reemplaza completamente a la población anterior (paso 6)
• Estrategias estacionarias: durante cada iteración se elige un subconjunto concreto de población basado en diferentes criterios (normalmente, aquellos mejor adaptados), se cruzan y los nuevos descendientes reemplazan a una parte de la población anterior

Normalmente los modelos estacionarios (aunque a priori pueden resultar más "discriminatorios") suelen tener una convergencia más rápida, al detectar mejor los individuos mejor preparados y seguir a partir de ellos, descartando al resto.

Hay que tener en cuenta, en cualquier caso, que los algoritmos genéticos son un modelo estocástico de obtención de resultados, es decir, el proceso es aleatorio, y por tanto, cada vez que lo ejecutemos podemos obtener resultados diferentes, aunque igualmente satisfactorios.

2. Algoritmos genéticos en Python con PyGAD

Existen algunas librerías específicas en Python para trabajar con algoritmos genéticos, tales como PyGAD o GeneAl. Son librerías open-source que podemos emplear para automatizar gran parte del proceso anteriormente descrito: indicar el número de iteraciones, la función de fitness, la población de individuos, y esperar el resultado final. En este documento veremos cómo usar PyGAD, aunque ambas son más o menos equivalentes.

2.1. Instalación y primeros pasos

La librería se instala como cualquier otra, usando el comando pip:

pip install pygad

Después, deberemos importar el módulo correspondiente en los ficheros donde vayamos a utilizarlo. Como veremos en los ejemplos a continuación, su uso es bastante sencillo: bastará con crear una instancia de la clase GA que incorpora la librería, con una serie de parámetros definidos, y después ponerla en marcha con su método run:

import pygad

instancia_ga = pygad.GA(...)
instancia_ga.run()

Una vez el proceso haya concluido, podremos recoger la mejor solución, o mostrar una gráfica de evolución del aprendizaje, con métodos como best_solution o plot_fitness.

2.2. Un ejemplo introductorio

Como primer ejemplo, veamos un caso simple: imaginemos que tenemos una expresión matemática como ésta:

y = a*x1 + b*x2 + c*x3 + d*x4

Y queremos, dados los valores de y, x1, x2, x3 y x4, determinar qué valores de a, b, c y d encajan en la ecuación. Por ejemplo, así:

30 = a*2 + b*3 + c*5 + d*7

Comenzaremos por importar las librerías que necesitemos (y que tendremos que tener previamente instaladas). Para este caso, además de PyGAD vamos a emplear NumPy para algunas operaciones con vectores numéricos:

import pygad
import numpy as np

Después, guardamos en dos variables los datos de entrada conocidos: el resultado final a obtener (valor de y, que podemos poner en 30 por ejemplo) y los valores de x1 a x4, en un vector o lista:

resultado = 30
valores_x = [2, 3, 5, 7]

La idea es que el algoritmo vaya generando cuartetos de coeficientes a, b, c, d, haciéndolos evolucionar hasta dar alguno que encaje o se aproxime mucho a la solución. Por lo tanto, a la hora de definir las características relevantes de cada individuo de nuestra población (lo que anteriormente hemos denominado alelos, que conforman el genotipo) usaremos también vectores de 4 elementos (tantos como valores de X).

2.3. La función de fitness

La función de fitness deberá devolver un valor numérico, que será mayor cuanto más se aproxime el resultado de la expresión al objetivo (30, en nuestro caso). Para PyGAD, la función de fitness debe recibir tres parámetros: la instancia al propio objeto PyGAD (no suele utilizarse), la posible solución que tenemos que evaluar (cada uno de los individuos de la población), y el índice que ocupa esa solución en la población (aunque este último parámetro casi nunca se utiliza). Podríamos definir una función de fitness como esta:

def fitness(instancia, solucion, indice):
    salida = np.sum(solucion*valores_x)
    resultado_fitness = 1.0 / (np.abs(salida - resultado) + 0.000001)    
    return resultado_fitness

Analicemos la función paso a paso:

• La primera línea realiza el cálculo de ax1 + bx2 + cx3 + dx4 para los valores de coeficientes_x que previamente hemos indicado, y para los valores de a...d que hay en la solucion que se está evaluando.
• Para ver lo bueno o malo que es ese cálculo, vemos su diferencia con respecto al resultado esperado (en valor absoluto). Como queremos que la función devuelva un resultado mayor cuanto menor sea esa diferencia, calculamos su inverso (dividimos 1 entre el resultado). Por si acaso la resta es justo 0, le sumamos una cantidad insignificante y constante de 0.000001.

2.4. El constructor. Inicialización del algoritmo

Ya lo tenemos todo preparado para crear nuestra instancia de algoritmo genético, a través de la clase GA de PyGAD:

instancia_ga = pygad.GA(num_generations=100,
                       sol_per_pop=10,
                       num_genes=len(valores_x),
                       num_parents_mating=2,
                       fitness_func=fitness,
                       mutation_type="random",
                       mutation_probability=0.6)

Explicamos para qué sirve cada uno de los parámetros:

• num_generations indica el número de iteraciones que se realizarán (100, en este caso)
• sol_per_pop indica cuántos individuos hay en la población de cada iteración (10 individuos)
• num_genes indica cuántos alelos hay en cada individuo (tantos como valores de x)
• num_parents_mating indica cuántos individuos se usarán en un cruce (dos es lo normal)
• fitness_func apunta a la función que se usará como fitness, y que debe cumplir el requisito que decíamos antes (recibir una posible solución y un índice como parámetro)
• mutation_type indica el tipo de mutación que se va a producir en las distintas generaciones. El tipo random que usamos en este ejemplo es el más habitual, y consiste en alterar al azar alguno de los alelos.
• mutation_probability indica la probabilidad de que cada uno de los alelos mute. Es un valor entre 0 y 1. Cuanto más cercano a 1 esté, más probabilidad de mutación habrá.

En principio, sólo son obligatorios los parámetros num_generations, num_parents_mating y fitness_func. Los otros son opcionales, y podemos elegir más, según consta en la documentación oficial.

2.5. Ejecución y resultados

Tras configurar nuestro algoritmo genético, lo ponemos en marcha con su método run, y luego podemos recoger los resultados con best_solution y mostrar una gráfica de convergencia con plot_fitness.

instancia_ga.run()

solucion, fitness_solucion, indice_solucion = instancia_ga.best_solution()
print(f"Parámetros de la mejor solución:\n{solucion}")
print(f"Fitness de la mejor solución: {fitness_solucion}")
print(f"Índice de la mejor solución: {indice_solucion}")

instancia_ga.plot_fitness()

El resultado que mostrará será parecido a este (la solución puede variar, al haber varias posibles)

Parámetros de la mejor solución: 
[ 2.09049163  2.45175166 -0.97830055  3.33434742]
Fitness de la mejor solución: 67.4145387749581
Índice de la mejor solución: 0

La gráfica que muestra en este caso es algo así (aunque también puede variar)

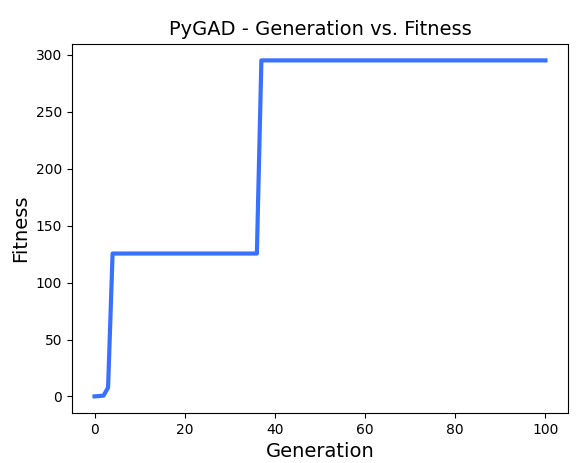
En este caso, podemos ver que ha habido dos "saltos" en la convergencia hacia la solución: uno al inicio del proceso y otro poco antes de llegar a la 40ª iteración. Esta gráfica también puede variar cada vez que ejecutemos el programa, al ser un método estocástico (aleatorio).

Sobre los resultados obtenidos podemos hacer algunas variaciones para ver cómo afectan al resultado final:

• Si incrementamos el tamaño de la población (parámetro sol_per_pop del constructor) obtendremos seguramente una convergencia más rápida (aunque un proceso más lento y más consumo de recursos)
• Si reducimos el número de iteraciones (parámetro num_generations) es posible que no alcancemos una solución apropiada, o también que ahorremos iteraciones cuando ya hemos alcanzado una.

Por ejemplo, podemos repetir el proceso con 30 individuos de población y 50 iteraciones, obteniendo esta otra gráfica de convergencia (mucho más rápida que la anterior):

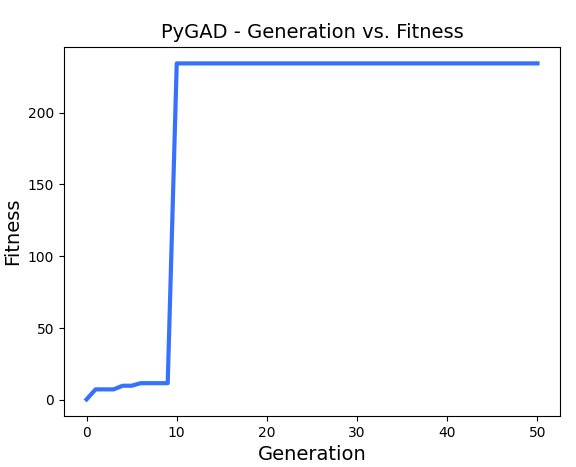
Aquí tienes el ejemplo completo de código para poderlo probar.

Ejercicio 1

Utiliza la librería PyGAD para implementar un algoritmo genético que resuelva una ecuación de segundo grado ax² + bx + c = 0, dados los coeficientes a, b y c. El algoritmo debe detectar dos soluciones DISTINTAS a la ecuación o, de lo contrario, indicar que no existen dos soluciones reales distintas.

3. Implementación manual de algoritmos genéticos

El uso de librerías como PyGAD puede resultar muy útil para programar rápidamente un algoritmo genético. Sin embargo, estas librerías pueden tener sus limitaciones; por ejemplo, a la hora de definir los parámetros de la población a estudiar. En el ejemplo anterior nos basamos en vectores de coeficientes numéricos, pero... ¿qué ocurre si nuestros individuos necesitan almacenar algo más de información? También a la hora de elegir la mutación, o el rango de valores en que movernos, se tiene alguna limitación, o su configuración no es tan sencilla.

En este apartado veremos cómo podemos programar nuestro propio algoritmo genético, definiendo a nuestra conveniencia las funciones para inicializar la población, generar los cruces, mutaciones, función fitness, etc.

Usaremos como hilo conductor el mismo ejemplo visto antes con la librería PyGAD (el ajuste de coeficientes de la expresión matemática), aunque la idea es que el código que hagamos sea fácilmente adaptable a otros supuestos.

3.1. Los individuos

Para representar los individuos de nuestro problema, vamos a definir una clase Individuo. Como atributos de dicha clase tendremos su vector de alelos (coeficientes numéricos reales) y le pasaremos como parámetro la función de fitness que queremos usar para evaluar al individuo. De esta forma, podemos invocar a la función desde el propio objeto, y guardarnos en un atributo la valoración o idoneidad de dicho individuo, dejándola precalculada.

class Individuo:
    def __init__(self, alelos, funcion_fitness):
        self.alelos = alelos
        self.fitness = funcion_fitness(self)

El atributo alelos se asume que será una lista o un vector unidimensional de NumPy. A la función de fitness le pasaremos el propio objeto Individuo, para que lo evalúe y devuelva su valoración, que guardamos en el atributo fitness de cada objeto.

3.2. Un algoritmo genético parametrizable

Vamos a definir ahora la clase que gestionará nuestro algoritmo genético, y en el constructor le añadiremos los parámetros que queramos configurar, igual que hacíamos en la clase GA de PyGAD. En concreto, usaremos estos parámetros:

• Tamaño de la población de individuos
• Tamaño del vector de alelos (número de coeficientes)
• Valor mínimo que permitimos que tome un alelo
• Valor máximo que permitimos que tome un alelo
• Si los valores de los alelos son discretos (enteros) o no (reales)
• Función de fitness que usaremos para evaluar a los individuos de la población. Ésta será una función externa, propia de cada problema, que le pasaremos al algoritmo, igual que hacemos en PyGAD
• Número de cruces que se harán en cada iteración
• Probabilidad de mutación de cada individuo que se genera por cruce
• Número de mutaciones en un individuo (cantidad de alelos que mutan). Podemos indicar que por defecto será 1.
• La población de individuos, que inicialmente será una lista vacía (de objetos de tipo Individuo)

Así, la clase y su constructor pueden quedar así:

class AlgoritmoGenetico:
    def __init__(self, tamano_poblacion, tamano_alelos, valor_minimo, valor_maximo, 
        valores_discretos, funcion_fitness, num_cruces, prob_mutacion, num_mutaciones = 1):
        self.tamano_poblacion = tamano_poblacion
        self.tamano_alelos = tamano_alelos
        self.valor_minimo = valor_minimo
        self.valor_maximo = valor_maximo
        self.valores_discretos = valores_discretos
        self.funcion_fitness = funcion_fitness
        self.num_cruces = num_cruces
        self.prob_mutacion = prob_mutacion
        self.num_mutaciones = num_mutaciones
        self.poblacion = list()
        self.generar_poblacion()

3.3. Generar y ordenar la población de individuos

A la hora de generar la población inicial de individuos, invocamos a un método llamado generar_poblacion al final del constructor anterior. Este método se valdrá de algunos de los parámetros del algoritmo para rellenar el vector poblacion con una cantidad de tamano_poblacion individuos, con tamano_alelo alelos cada uno, con valores entre valor_minimo y valor_maximo. Para generar cada alelo aleatorio, usaremos una función adicional (privada de la clase) que generará un número real o entero, dependiendo del atributo valores_discretos:

def __generar_valor(self):
    if self.valores_discretos:
        return np.random.randint(self.valor_minimo, self.valor_maximo+1)
    else:
        return np.random.uniform(low = self.valor_minimo,
                high = self.valor_maximo, size = 1)[0]

La función generar_poblacion quedaría de este modo:

def generar_poblacion(self):
    while len(self.poblacion) < self.tamano_poblacion:
        alelos = np.array([self.__generar_valor() for i in range(self.tamano_alelos)])
        self.poblacion.append(Individuo(alelos, self.funcion_fitness))

Como vemos, generamos un vector aleatorio de números de tamaño tamano_alelos, generando cada dato con una llamada a generar_valor. Con dicho vector creamos un objeto Individuo, pasándole la función de fitness para que se evalúe y guarde su valoración.

La población de individuos la necesitaremos ordenar periódicamente según su idoneidad (fitness). Podemos usar un método como este:

def ordenar_poblacion(self):
    self.poblacion.sort(key=lambda x: x.fitness, reverse=True)

3.4. Selección, cruce y reemplazo de individuos

Vamos a implementar ahora los métodos que nos permitirán seleccionar dos individuos de la población y cruzarlos para crear otro nuevo.

A la hora de seleccionar dos individuos como progenitores de un nuevo individuo, debemos procurar que estos dos candidatos sean seleccionados aleatoriamente de entre los mejor valorados. Para hacer esto, podemos emplear la librería random de Python (la importamos con import random), y usar su método choices (información aquí). Este método permite definir varios parámetros, pero nos interesan tres:

• El conjunto de datos de entre los que tenemos que seleccionar alguno. En nuestro caso, será el conjunto de individuos, o los índices de dichos individuos en la población (de 0 al tamaño de la población)
• Los pesos que tiene cada individuo, que determinarán la probabilidad con que será elegido. A mayor peso, mayor probabilidad. Este parámetro consiste en un vector del mismo tamaño que el anterior, donde se indica el peso que tiene cada candidato. Podemos usar como peso de cada candidato su propio fitness, de modo que tendrán más probabilidad de ser elegidos los que tengan más fitness, y mucha más probabilidad los que tengan mucho más fitness.
• Cuántos elementos queremos seleccionar. En este caso, los iremos seleccionando de uno en uno.

Usando esto, nuestra función para seleccionar dos individuos de la población (distintos), con una probabilidad acorde a su idoneidad, puede quedar así:

def seleccionar_individuos(self):
    # Indices de los individuos de la población
    indices = range(0, self.tamano_poblacion)
    # Peso para cada individuo según su fitness
    pesos = [x.fitness+0.0000001 for x in self.poblacion]
    # Elegimos el primer individuo
    individuo1 = random.choices(indices, weights=pesos, k = 1)[0]
    # Elegimos al segundo individuo de entre los restantes
    indices_restantes = [i for i in indices if i != individuo1]
    individuo2 = random.choices(indices_restantes, weights=[pesos[i] for i in indices_restantes], k=1)[0]
    return individuo1, individuo2

Nota

Sumamos 0.0000001 en los pesos por si acaso todos los fitness son 0, ya que la función random.choices necesita que la suma de pesos no sea 0.

Una vez tenemos dos individuos seleccionados, debemos cruzarlos para generar otro. La función de cruce puede quedar así, pasándole como parámetro los índices de los individuos seleccionados:

def cruzar(self, individuo1, individuo2):
    nuevos_alelos = np.zeros(self.tamano_alelos)
    for i in range(self.tamano_alelos):
        aleatorio = np.random.rand()
        if aleatorio >= 0.5:
            nuevos_alelos[i] = self.poblacion[individuo1].alelos[i]
        else:
            nuevos_alelos[i] = self.poblacion[individuo2].alelos[i]
    return nuevos_alelos

La función crea un vector de alelos del mismo tamaño que el resto, inicialmente a ceros. Después, va alelo a alelo, y genera un número aleatorio de 0 a 1. Si es mayor de 0.5 toma el alelo del individuo 1, y si no, del individuo 2.

La función de reemplazo de individuos tomará un individuo, y una posición en la población, y directamente reemplazará el elemento de esa posición por el nuevo individuo. En el algoritmo general veremos cómo encajarla exactamente.

def reemplazar(self, hijo, indice):
    self.poblacion[indice] = hijo

3.5. Las mutaciones

Las mutaciones consistirán en alteraciones aleatorias de alelos de los nuevos individuos que se vayan generando. Para ello podemos emplear esta función:

def mutar_individuo(self, alelos):
    for i in range(self.num_mutaciones):
        nuevo_valor = self.__generar_valor()
        alelo_seleccionado = np.random.randint(self.tamano_alelos)
        alelos[alelo_seleccionado] = nuevo_valor

La función recibe un vector de alelos (generado con la función cruzar) y le aplica tantas mutaciones como esté indicado en el atributo num_mutaciones del algoritmo. Para cada iteración, generamos un valor al azar dentro de los límites establecidos, elegimos un alelo aleatoriamente y reemplazamos su antiguo valor por el nuevo generado.

3.6. El proceso general

Vamos a aplicar ahora el proceso general del algoritmo genético, adaptando el proceso que hemos visto al inicio de este documento. Lo recordamos aquí:

1. Inicializamos t = 0
2. Inicializamos una población inicial de individuos P(t=0). Normalmente, de forma aleatoria.
3. Mientras no se cumpla una condición de parada
4. Evaluar P(t)
5. t = t + 1
6. Seleccionar P(t) desde P(t-1)
7. Cruzar P(t)
8. Mutar aleatoriamente algún(os) individuo(s) del cruce
9. Reemplazar población

Los pasos 1 y 2 ya los hemos dado previamente, ya que en el constructor hemos generado una población inicial llamando a generar_poblacion. Por tanto, este método debe ocuparse del bucle del paso 3. Podríamos plantearlo así:

def iniciar_proceso(self, iteraciones, verbose=False):
    for i in range(iteraciones):
        # Evaluamos la población
        self.ordenar_poblacion()
        # Mostramos información de la iteración si procede
        if verbose:
            print("Iniciando iteración", i+1, ", fitness = ",
                    self.poblacion[0].fitness)
        for j in range(self.num_cruces):
            # Seleccionar
            individuo1, individuo2 = self.seleccionar_individuos()
            # Cruzar
            nuevos_alelos = self.cruzar(individuo1, individuo2)
            # Mutar. Mutamos si entra en la probabilidad
            resultado_probabilidad = np.random.rand()
            if resultado_probabilidad < self.prob_mutacion:
                self.mutar_individuo(nuevos_alelos)
            # Se conforma el nuevo individuo
            hijo = Individuo(nuevos_alelos, self.funcion_fitness)
            # Reemplazar población
            self.reemplazar(hijo, self.tamano_poblacion - 1 - j)
    self.ordenar_poblacion()
    return self.poblacion[0]

El método recibe dos parámetros: el número de iteraciones o generaciones que hay que realizar, y un parámetro verbose que, si está a True, indicará que queremos ver información de cómo va el proceso por pantalla (de eso se encarga el if que hay al inicio del bucle).

Al final del proceso, se ordena la población según su fitness y se devuelve el mejor individuo (posición 0).

3.7. Aplicando el algoritmo al proceso

Vamos a aplicar ahora todo este algoritmo a nuestro ejemplo. La función de fitness que usaremos para evaluar los individuos tendrá un comportamiento similar a la anterior. Recibirá como parámetro cada individuo de la población, y devolverá un número que será mayor cuanto mayor sea la idoneidad de ese individuo.

def fitness(solucion):
    salida = np.sum(solucion.alelos*valores_x)
    resultado_fitness = 1.0 / (np.abs(salida - resultado) + 0.000001)    
    return resultado_fitness

Ejercicio 2

Construye un proyecto Python que utilice el algoritmo genético creado en este apartado para resolver el problema de los coeficientes, con los mismos datos de entrada que en el caso de PyGAD. Prueba a ajustar distintos parámetros (iteraciones, tamaño de población, probabilidad de mutación) y observa cómo afectan al resultado final.

4. Aplicaciones de los algoritmos genéticos

Los algoritmos genéticos se pueden emplear en multitud de ámbitos del mundo de la computación. Vamos a ver aquí algunos ejemplos.

• En el aprendizaje de todo tipo de juegos y videojuegos, tanto juegos de tablero convencionales (tres en raya, ajedrez, backgammon) como videojuegos simples tipo Arkanoid, o Flappy Bird a otros más complejos como Super Mario Bros. En algunos de estos casos se combina la potencia de las redes neuronales con los algoritmos genéticos, haciendo que éstos ayuden a entrenar a aquéllas. De esta forma, se puede disponer de una población inicial de redes neuronales, e irlas evolucionando para ver cuál de ellas alcanza mejores resultados en un problema dado.
• Además, los algoritmos genéticos pueden resultar muy útiles para elegir un subconjunto relevante de características dentro de un conjunto de datos, y así poder aplicar el mejor subconjunto de características a problemas de regresión, clasificación, etc.
• También pueden utilizarse para optimizar la estructura de modelos de deep learning, es decir, determinar qué estructura de redes neuronales profundas es la más adecuada para un problema determinado, a nivel de número de capas, conexiones, funciones de activación, etc.
• Son también aplicables a problemas de búsqueda y optimización. Ejemplos típicos pueden ser el de la mochila discreta, o el viajante de comercio. Pero también pueden ayudar a encontrar soluciones en cuestiones más cotidianas, como la mejor forma de secuenciar un conjunto de tareas, o de colocar a los invitados a una boda. En estos casos, hay que tener presente que NO se garantiza obtener una solución óptima, al tratarse de un método estocástico.
• Cualquier tarea de aprendizaje por refuerzo, donde el sistema dé una valoración de lo bien o mal que se está resolviendo un problema, puede plantearse en términos de algoritmos genéticos. Basta con delimitar bien qué parámetros va a usar el problema, y la función de valoración o fitness.

4.1. Ejemplo: el problema de la mochila

El problema de la mochila consiste en averiguar cuál es el mejor conjunto de objetos que podemos incluir en una mochila, dadas unas restricciones. Se parte de un conjunto de objetos con una serie de pesos p = [p1, p2, ... pN], y una serie de valores asociados v = [v1, v2, ... vN]. Tenemos, por otra parte, una mochila con una capacidad de carga máxima P. El problema trata de averiguar cuál es el conjunto de objetos más valioso que podemos cargar en la mochila sin pasarnos de peso.

Podemos plantear los datos básicos del problema: el vector de pesos y el de valores, junto con el peso máximo soportado por la mochila. Por ejemplo:

pesos = [100, 60, 210, 140, 85, 180, 30]
valores = [10, 8, 30, 18, 9, 20, 6]
peso_maximo = 300

A la hora de plantear el problema, podemos definir el conjunto de alelos de cada individuo como un vector de ceros y unos, del mismo tamaño que el vector de pesos o valores. Un 0 indicará que no cargamos ese objeto en la mochila, y un 1 indicará que sí. Por ejemplo, este vector:

[1, 0, 0, 1, 0, 0, 1]

Indica que llevaríamos el primer objeto (peso 100, valor 10), el cuarto objeto (peso 140, valor 18) y el último (peso 30, valor 6), para un peso máximo de 270 (no excedemos el máximo) y un valor final de 34.

Ejercicio 3

Crea un proyecto ProblemaMochila y, usando PyGAD por un lado y el algoritmo genético personalizado que hemos desarrollado en el apartado anterior por otro, intenta resolver el problema de la mochila. Puedes usar los datos de entrada que hemos puesto como ejemplo. Define una función de fitness adecuada, e invoca al algoritmo con los parámetros apropiados para encontrar una solución al problema.

Nota

En el caso de PyGAD, deberás indicar que los genes o alelos deben ser de tipo entero, con un valor mínimo de 0 y un valor máximo de 2 (para que incluya el 1). Echa un vistazo a los parámetros gene_type, init_range_low e init_range_high de la documentación del constructor

Ejercicio 4

Tenemos que realizar una lista de tareas. Cada tarea lleva asociado un tiempo en minutos que cuesta realizarla, y unas dependencias (qué tareas hay que finalizar antes de comenzar con una determinada). Utiliza algoritmos genéticos para, dada la lista de tiempos y dependencias de las tareas, obtenga una solución con el máximo número de tareas que se pueden realizar en un tiempo máximo determinado.

Pista

Puedes representar los tiempos de las tareas en un vector, y las dependencias en un vector de vectores, donde en cada posición se muestran las tareas que hay que completar antes de iniciar esa, o lista vacía si no hay dependencias:

tiempos = [30, 15, 20, 25, 40, 10, 15, 5]
dependencias = [
    [],
    [0, 3],
    [1, 3],
    [4],
    [],
    [4],
    [4, 5],
    [0, 2, 6]
]
tiempo_maximo = 120

En el ejemplo anterior, la tarea 0 no tiene dependencias y dura 30 minutos, la tarea 1 dura 15 minutos, pero hay que completar antes la 0 y la 3, etc.

Ejercicio 5

Haremos ahora una nueva versión del ejercicio anterior donde lo que nos interesa es que el algoritmo nos plantee una secuencia correcta para resolver las tareas, dadas sus dependencias. Por ejemplo, siguiendo el ejemplo anterior, la tarea 1 no puede hacerse antes que la 0. La solución deberá estar formada por una secuencia de números de 0 a N-1 (siendo N el número total de tareas), indicando qué tarea se realiza en cada posición.

Nota

En este caso, puede interesar alterar el código del algoritmo genético para asegurarnos de que los individuos van a tener alelos discretos y distintos entre sí, o bien definir una función de fitness que penalice con 0 a los individuos con alelos iguales en posiciones distintas (lo que indicaría que se va a realizar más de una vez la misma tarea).