Introducción a las redes neuronales y el deep learning¶

1. ¿Qué es el deep learning?¶

El deep learning es una rama dentro del campo del machine learning que produce un aprendizaje y conocimiento más profundos. ¿Qué queremos decir con esto? Imaginemos que desarrollamos un sistema al que le pasamos una serie de características de unas flores (color, tamaño de los pétalos, época de florecimiento, etc) y nos identifique de qué flor se trata.

Ahora vayamos un paso más allá... ¿qué ocurriría si al sistema le pudiéramos pasar directamente una foto de una flor y él mismo fuera capaz de extraer las características relevantes (colores, líneas, tamaños...) e identificar de qué flor se trata? En este segundo caso el sistema ha generado un conocimiento o procesamiento más profundo de los datos de entrada, ha sido capaz de extraer unas características relevantes que, en el primer caso, hemos tenido que proporcionarle nosotros mismos.

El primer ejemplo correspondería a un caso de machine learning simple: proporcionamos una serie de datos de entrada y el sistema produce un resultado. El segundo entra dentro del campo del deep learning: el sistema es capaz de deducir o extraer características de datos inicialmente sin procesar, para producir el mismo resultado.

La técnica más habitualmente empleada dentro de la rama del deep learning son las redes neuronales profundas, entendiendo como profundas el hecho de que estén compuestas por varias capas, lo que les permitirá jerarquizar las características principales de los datos de entrada. En este documento vamos a ver una introducción teórica a qué son y cómo funcionan las redes neuronales.

2. Concepto de red neuronal¶

Una red neuronal, también llamada red neuronal artificial es un modelo computacional que trata de imitar las conexiones neuronales de un cerebro humano. Para ello se definen una serie de neuronas artificiales conectadas entre sí para transmitirse información, de forma que la información entra a la red neuronal por unos puntos de entrada y sale de ella produciendo un resultado.

Las redes neuronales siempre se organizan en capas, con una capa de entrada que recibe la información, una capa de salida que produce un resultado, y una serie de capas intermedias u ocultas que se encargan de procesar la información. Cada neurona se conecta a todas las neuronas de la capa anterior, de modo que los enlaces entre neuronas transmiten unos valores que pueden modificar el resultado que se produzca.

La información se le proporciona a la red a través de su capa de entrada, y esos datos se van procesando por todas las conexiones entre neuronas, produciendo un resultado o salida. Así, por ejemplo, podemos pasar como entrada los datos de una imagen y que la salida catalogue o clasifique la imagen (indique qué es). O bien pasarle unos valores numéricos de entrada y que muestre un valor numérico de salida (por ejemplo, una estimación de temperatura futura a partir de unos datos de entrada).

2.1. Algo de historia¶

Repasemos brevemente los principales hitos históricos que han tenido un impacto importante en el desarrollo de las redes neuronales artificiales.

El primer gran hito lo ubicamos en 1943, cuando McCulloch y Pitt desarrollan el concepto de red neuronal
En 1958, Rosenblatt desarrolla el concepto de perceptrón, cada una de las unidades que compone una red neuronal, explicando su funcionamiento y conexión entre las entradas y la salida.
En 1974, Werbos y otros investigadores idean la estrategia del backpropagation, que se empleará en las redes neuronales para reajustar su funcionamiento y mejorar sus resultados.
Más tarde, en 1986, Rumelhart, Hinton y Williams terminarían de perfilar esta técnica de backpropagation, junto con el concepto de perceptrón multicapa, mediante el que se pueden construir redes neuronales más profundas, con múltiples capas intermedias u ocultas.
Seguimos en 1986, donde se desarrolla la idea de las redes neuronales recurrentes, en las que las neuronas de una capa no sólo pueden conectarse con las de la capa siguiente, sino con las de su misma capa o capas anteriores. Esto ampliará aún más el campo de aplicación de estas redes, pudiendo ser capaces de incluir el factor "tiempo" o "secuencia" en sus predicciones.
Las redes neuronales sufrieron un período de estancamiento a finales del siglo pasado, hasta que los avances en hardware en cuanto a computación paralela permitieron ejecutar en mucho menos tiempo tareas que anteriormente requería de varias horas, e incluso días. Además, el desarrollo de sistemas de big data permitirá almacenar grandes cantidades de datos, muy útiles para entrenar y preparar las redes neuronales.

2.2. Más sobre las entradas y las salidas¶

Hemos visto que una red neuronal dispone de una capa de entrada con la que le proporcionamos la información externa que necesita para trabajar, y una capa de salida a través de la cual emite un resultado. Pero... ¿qué tipos de entradas y salidas podemos utilizar? Veamos algunos ejemplos:

Podríamos desarrollar una red neuronal que nos ayude a calcular el salario que debería tener un trabajador en base a ciertos datos de entrada, como años de experiencia en el puesto de trabajo, formación complementaria, etc. Los datos de entrada serían cada uno de los valores (cuantificables) que podamos considerar relevantes de cada trabajador (años de experiencia, número de horas de formación específicas sobre un tema, etc). Tendremos tantas neuronas en la capa de entrada como datos diferentes queramos captar de cada trabajador. Por otra parte, la salida se dedicará a emitir un valor numérico continuo (salario recomendado), por lo que bastará con una única neurona de salida.
Otro sistema podría consistir en clasificar una serie de imágenes en varias categorías. Por ejemplo, identificar qué imágenes corresponden a flores, a perros, casas o personas. En estos casos, la entrada estará compuesta por tantas neuronas como "valores" tengan las imágenes, y cuando hablamos de "valores" nos referimos a unidades de información. Podríamos poner una neurona por cada píxel, por ejemplo, pero si el píxel está formado por varios colores, quizá interese también una neurona para cada color (rojo, verde, azul). En cuanto a la salida, queremos determinar una clasificación, y en este caso lo habitual será tener en la capa de salida una neurona por cada categoría clasificable. En nuestro ejemplo (flores, perros, casas, personas) harían falta 4 neuronas, de forma que se activará aquella que se corresponda con la categoría asignada por la red a la imagen de entrada.
Un tercer sistema podría consistir en un asistente que ayude a una entidad financiera a evaluar la idoneidad de clientes para la concesión de préstamos. Recibiría como datos de entrada los datos relevantes del cliente (edad, salario anual, cantidad solicitada, otras cargas...) y produciría como salida un veredicto de si es adecuado o no formalizar el préstamo. Nuevamente, tendremos tantas entradas como datos necesitemos del cliente, y la respuesta en este caso es binaria ("sí" o "no"). Podría bastar con una única neurona en la capa de salida que se ponga a 0 o 1, por ejemplo.

Como vemos, la morfología de la capa de entrada y de salida va a depender de los datos que esperamos recibir y del tipo de resultado que debemos generar. Pero, en todos los casos, hay que tener presente que dispondremos de una gran cantidad de datos de entrada (una gran cantidad de datos de trabajadores, o de imágenes a clasificar, o de clientes del banco) y los pasaremos de uno en uno a la red. Es decir, pasaremos los datos de un trabajador y obtendremos una respuesta para ese trabajador, luego pasamos el siguiente y obtenemos una respuesta... y así sucesivamente. A medida que la red va produciendo estos resultados, se irán contrastando con los que debería haber producido, y la propia red será capaz de ajustar sus parámetros para dar resultados más ajustados en la próxima tanda de intentos.

3. Componentes y funcionamiento de una red neuronal¶

Pasemos ahora a detallar los diferentes elementos que conforman una red neuronal y las relaciones que existen entre ellos.

3.1. La neurona o perceptrón¶

Cada neurona de una red neuronal se denomina perceptrón, y tiene una estructura como la siguiente:

Como podemos ver, cada perceptrón o neurona de la red recibe una serie de entradas x₁ .. x_n, que son ponderadas con una serie de pesos w₁ .. w_n, de modo que, en cada perceptrón, se le da más peso o importancia a unas entradas que a otras. Además, internamente el perceptrón suma al resultado ponderado de sus entradas un umbral, sesgo o bias b. De este modo, podemos considerar la salida de una neurona como una combinación o función lineal de sus entradas, sumándole el bias:

y = w₁x₁ + ... + w_nx_n + b

Podemos ver así el perceptrón como un elemento que define una función lineal (una recta). Esto nos puede servir, por sí solo, para identificar dos tipos de elementos en un problema (los que queden a ambos lados de la recta), o para definir un mecanismo de regresión lineal, y usar la recta para predecir un valor y dado(s) otro(s) x.

El resultado final que produce la neurona se le pasa a una función de activación, que es la que determina la salida final que produce dicho perceptrón. Hablaremos a continuación de dicha función de activación, pero, en lo que a un perceptrón se refiere, nos podemos quedar con la idea de que procesa varios datos de entrada y produce un único resultado, aplicando una combinación lineal de sus entradas.

3.2. Las conexiones y pesos¶

Las salidas de los perceptrones de una capa conformarán las entradas de los perceptrones de la capa siguiente, y así sucesivamente, hasta llegar a la capa de salida, donde cada perceptrón emite una salida, y la combinación de todas las salidas será la respuesta de la red neuronal a la información proporcionada como entrada.

Los pesos de las conexiones entre neuronas determinarán el resultado final producido por cada perceptrón, y por tanto, el resultado final emitido por la red. Ajustar estos pesos es la tarea crucial de estos sistemas, lo que determina si la red se ajusta a lo que buscamos y resuelve el problema que le proponemos de forma adecuada. Esto se consigue en la fase de entrenamiento, como veremos a continuación.

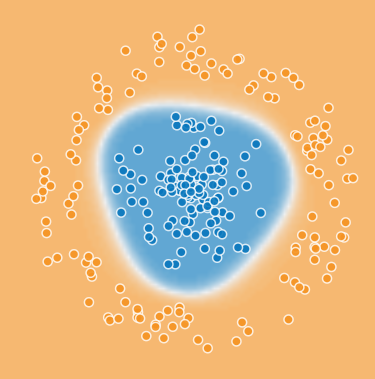
¿De qué sirve conectar varios perceptrones? Hemos visto que el uso de un único perceptrón sólo sirve para hacer una división o ajuste lineal de un espacio de resultados. Combinar varios perceptrones nos servirá, como veremos, para establecer delimitaciones o identificaciones no tran triviales, como ésta:

3.3. La salida y la función de coste¶

Mediante esta combinación de pesos y valores de entrada, combinadas con su función de activación, cada neurona "pasa" un resultado a las neuronas de la siguiente capa, hasta que, en la capa de salida, las neuronas producen un resultado.

La diferencia entre el resultado producido por la red y el que se debería haber producido determinará lo bien o mal que la red ha realizado sus cálculos. Para calcular esta diferencia se utiliza una función de coste, también llamada función de pérdida o loss, y el objetivo de la red será minimizar el resultado de esta función de coste.

Existen diferentes funciones de coste que podemos aplicar en nuestras redes neuronales. Algunas de las más habituales son:

Error absoluto medio (MAE, Mean Absolute Error): consiste en calcular la diferencia en valor absoluto entre el valor real y y el valor estimado y', y calcular la media de esta diferencia para las n entradas que proporcionemos a la red.

MAE = sum(|y - y'|) / n

Error cuadrático medio (MSE, Mean Squared Error): consiste en calcular el cuadrado de la diferencia entre los dos valores anteriores, para cada entrada pasada a la red, y calcular la media de las n entradas.

MSE = sum((y - y')²) / n

Error cuadrático logarítmico medio (MSLE, Mean Squared Logarithmic Error): es similar al anterior, pero aplica el logaritmo sobre la diferencia. Se utiliza cuando no queremos penalizar tanto los errores como en el caso anterior. Dado que el logaritmo de un valor es inferior al valor en sí, la diferencia entre logaritmos también será inferior, y por tanto el error cometido será menor:

MSLE = sum((log(y+1) - log(y'+1))²) / n

Sobre las dos funciones anteriores se pueden aplicar variantes, como la raíz cuadrada (RMSE y RMSLE, respectivamente), que consisten en calcular la raíz cuadrada del valor obtenido con las fórmulas anteriores
La entropía cruzada (cross-entropy) es una función de coste empleada en tareas de clasificación. Mide de algún modo la diferencia de información entre la clasificación emitida por la red y la real. Cuanto más se asemejen, menor será la entropía.

3.4. El entrenamiento¶

Inicialmente los pesos de las conexiones entre neuronas se asignan aleatoriamente, ya que, en principio, no se sabe cuáles van a ser los valores adecuados. El entrenamiento consiste en ir ajustando esos pesos para que las salidas que ofrece la red se ajusten lo máximo posible a las que consideramos correctas. En la gran mayoría de los casos, esto consiste en un sistema de aprendizaje por refuerzo, donde disponemos de una batería de datos de entrada con resultados correctos, de forma que los pasamos a la red, contrastamos las salidas emitidas con las esperadas y, en base a la función de coste, la red reajusta los pesos para el siguiente intento.

Ajuste de los pesos

¿Cómo se reajustan los pesos de una tanda de entradas para la siguiente? A través de un método denominado backpropagation o retropropagación. Esta técnica fue introducida en el campo de las redes neuronales, junto con la idea del perceptrón multicapa, en los años 70-80, y supuso un importante avance en este campo de la IA, ya que permite ajustar los pesos de las conexiones al error cometido en una sola pasada por la red, y acercarse poco a poco al error mínimo, en lugar de la técnica que se utilizaba hasta entonces, consistente en ir variando aleatoriamente los pesos y probando cada vez para ver si se ajustaba mejor al resultado esperado.

El método funciona en dos etapas:

Una primera etapa forward o hacia adelante, donde le pasamos los datos de entrada a la red, se calculan las salidas correspondientes y se obtiene el resultado final producido con los pesos actuales de las conexiones. Con esto se puede calcular el error cometido por la red en su estimación, en cada una de sus salidas, como la diferencia entre lo que debería haber producido y lo que ha producido realmente (función de coste).

Una segunda fase hacia atrás o backward, donde el error calculado se propaga hacia atrás, desde la capa de salida. Cada neurona recibe la fracción del error que ella misma ha cometido y, en función de eso, ajustará los pesos de las conexiones.

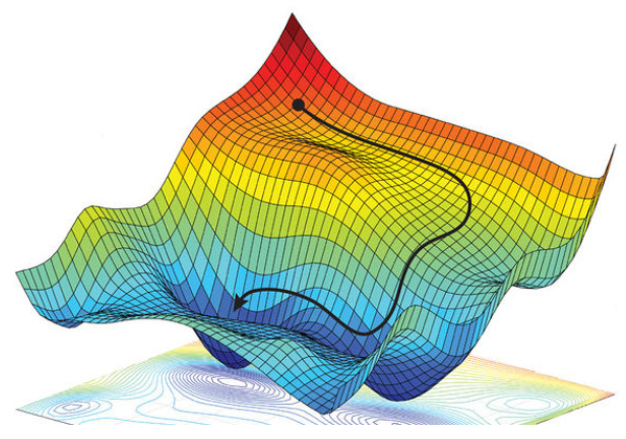
La técnica más habitual para este ajuste es el descenso por gradiente, que se basa en ajustar los pesos en busca de un mínimo error. Se pasan todos los registros de entrada de que se dispone para entrenar la red, se comparan las salidas emitidas con las esperadas y se calcula con ello el error cometido, usando la función de coste escogida. Esa función de coste ayuda a detectar cómo de grande es el error, para actualizar los pesos de las conexiones en la etapa de retropropagación e ir minimizando dicho error.

Sobre esta técnica se pueden aplicar distintas variantes u optimizaciones, que básicamente lo que hacen es modificar el learning rate o tasa de aprendizaje, un factor que determina la longitud de los pasos que se dan buscando el mínimo. Así, habrá estrategias que lo encuentren más rápidamente, otras que tarden más, y otras que den pasos tan grandes que nunca lleguen a encontrarlo. Pero la idea en general es, desde el resultado que se ha obtenido, encontrar el camino que poco a poco nos lleve al punto de mínimo error. Algunos ejemplos de optimizadores que veremos en otras sesiones son el descenso por gradiente estocástico (SGD), el optimizador adam, etc.

3.5. La función de activación¶

La función de activación es la que determina la salida final que produce cada neurona, modulando el resultado de la combinación lineal de pesos y entradas. La idea final es que el valor final esté limitado a un rango y/o que se agrupe en ciertos valores concretos.

Existen diferentes tipos de funciones de activación, y podemos elegir unas u otras dependiendo del tipo de salida requerido. Es más, podemos elegir diferentes funciones de activación para las diferentes capas o niveles de la red, ya que puede interesar que en algunas capas se tenga un tipo concreto de salida, y en otras otro.

Algunos ejemplos de funciones de activación

Algunas de las funciones de activación más habituales que podemos usar en nuestras redes neuronales son las siguientes:

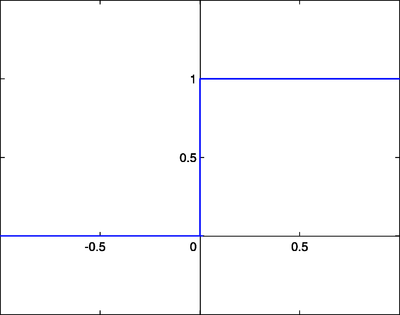
Función escalonada. Limita la salida de una neurona a dos valores: uno si no se llega a un umbral determinado, y otro si se sobrepasa dicho umbral. No es una función útil en muchos casos, porque limita mucho las posibilidades de "moldear" la salida.

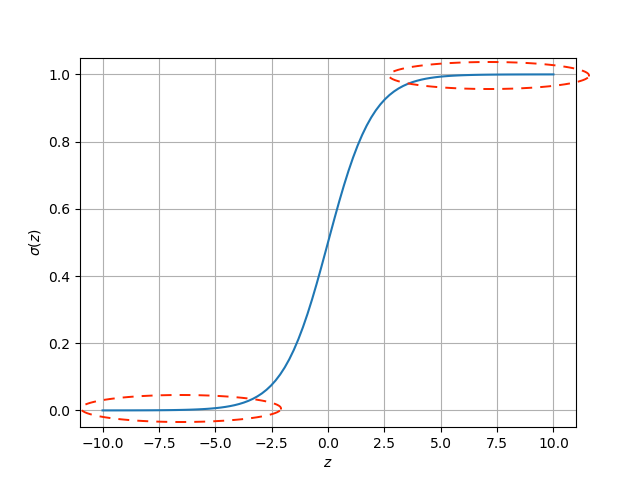
Función sigmoide o sigmoidea establece una curva entre 0 y 1 de modo que los valores excesivamente grandes se agrupan en torno a 1, y los excesivamente pequeños en torno a 0, pero en medio se tiene una transformación no lineal. Su uso facilita el proceso de backpropagation buscando minimizar el error, ya que es derivable y podemos encontrar la pendiente para el descenso por gradiente. Pero su cálculo es costoso. Puede usarse en problemas de clasificación binaria (dos tipos de resultados finales), en lugar de la escalonada.

Función de tangente hiperbólica, similar a la anterior, pero con un rango de entre -1 y 1.

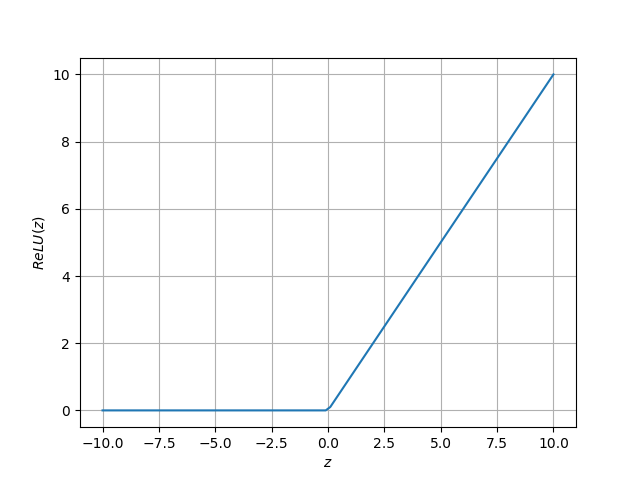
Función de unidad rectificada lineal (ReLU). Se comporta como una función lineal si es positiva, y constante a 0 si es negativa. Es fácilmente computable, pero no es derivable. Se utiliza con frecuencia por su rapidez computacional, y en los casos en los que queramos "desactivar" neuronas si el resultado no alcanza un cierto umbral.

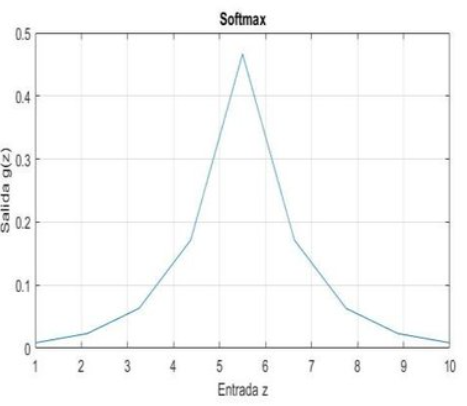
Función softmax, empleada para categorizar resultados en distintos grupos. Suele emplearse en la capa de salida de ciertas redes, dedicadas a clasificar datos de entrada. Se define una neurona de salida por cada clase, con una función softmax que asigna una probabilidad de 0 a 1 de pertenecer a dicha clase.

Ejemplos de uso

El uso de una u otra función de activación dependerá del tipo de comportamiento o clasificación que queramos alcanzar en nuestra red neuronal. Podemos definir una función de activación diferente para cada capa de nuestra red, y así dar forma al resultado final, dependiendo de si queremos una clasificación lineal, curva, etc. Lo iremos viendo con algunos ejemplos más adelante, pero daremos ahora algunos ejemplos introductorios.

Imaginemos, para empezar, una red que debe determinar si se le concede un préstamo a un cliente de un banco o no. En este caso interesará modular la salida en dos valores posibles sí/no o 0/1. Nos puede interesar una función de activación escalonada, o también una sigmoidea si queremos suavizar la respuesta en forma de probabilidad (un valor cercano a 1 indicaría que el préstamo es aconsejable, uno cercano a 0 que no es recomendable).
Imaginemos, por otro lado, un sistema de clasificación de imágenes en categorías. En este caso en la capa de salida puede interesar tener una función de activación softmax (una neurona por cada categoría, con función de activación softmax). Así, la salida mostrará la probabilidad de que la imagen de entrada sea de cada una de las categorías referidas. Además, en este caso podría ser interesante que las capas intermedias utilicen una función de activación ReLU, para que se desactiven o activen las neuronas en función de si detectan o no ciertas características propias de ciertas categorías de imágenes. Por ejemplo, si la imagen no es de una persona, que se desactiven las neuronas especializadas en detectar rasgos faciales, como ojos o bocas.

3.6. Resumen¶

Enlazamos a continuación unos vídeos externos que explican muy bien los conceptos importantes que hemos tratado hasta ahora.

Aquí tenemos un vídeo que explica el comportamiento de una neurona, cómo funcionan o se ajustan sus pesos y los problemas que es capaz de resolver
Aquí se explican los beneficios de conectar varias neuronas, y cómo podemos adaptar el comportamiento de la red a diferentes tipos de salidas usando funciones de activación.
Adicionalmente, aquí puedes consultar una explicación intuitiva de en qué consiste el algoritmo de backpropagation. En este vídeo se explica también en qué consiste la técnica del descenso por gradiente, usada en backpropagation para minimizar el error cometido.

4. Tipos de redes neuronales¶

Existen distintos tipos de redes neuronales, que se aplican dependiendo del resultado que se esté buscando. En próximos documentos analizaremos con detalle algunas de ellas, pero una primera clasificación podría ser esta:

Redes neuronales artificiales. Redes "tradicionales", con una o varias capas ocultas (estas últimas llamadas redes o perceptrones multicapa), que se emplean para tareas generales de regresión o clasificación.
Redes neuronales convolucionales. Utilizadas para tareas de visión o procesamiento de imágenes (clasificación de imágenes, detección de objetos en imágenes, etc)
Redes neuronales recurrentes. Empleadas para analizar series temporales de datos. Así se puede predecir el valor de una determinada serie en un futuro, o analizar un conjunto de palabras para comprender extraer su significado general.
Auto-encoders. Empleadas para procesar o transformar los propios datos de entrada. Pueden utilizarse para mejorar imágenes, por ejemplo.
... etc.