Redes recurrentes¶

En este documento abordaremos el estudio de las redes neuronales recurrentes (RNN, Recurrent Neural Networks), útiles cuando interviene el factor tiempo en el estudio de los datos, o cuando queremos procesar una secuencia de datos de entrada donde el orden entre ellos es un elemento a tener en cuenta.

1. Presentando el problema a resolver¶

Para ilustrar el tipo de problema que pretenden resolver las redes recurrentes, veamos un ejemplo sencillo. Imaginemos una secuencia de los números del 1 al 5 (es decir: 1, 2, 3, 4, 5) que se repite consecutivamente en el tiempo:

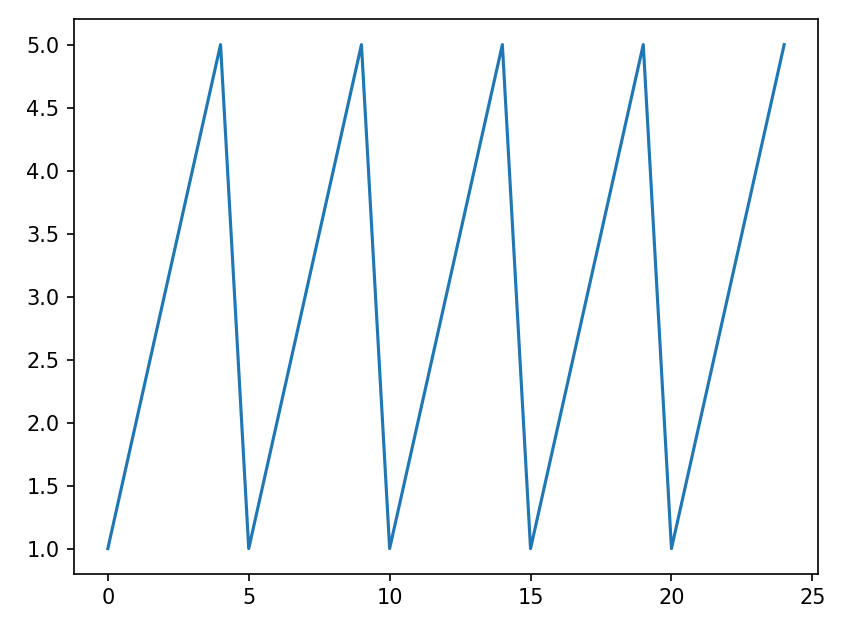
Vamos a plantear una red neuronal convencional a la que le pasemos una secuencia consecutiva de 1000 de estos valores, e intente aprender a predecir el siguiente valor. Construimos primero el conjunto de valores objetivo y como una secuencia 1-5 repetida 1000 veces. Las x correspondientes serán los números de orden de cada valor, del 0 en adelante (o del 1 en adelante, como prefiramos):

import numpy as np
from keras.models import Sequential
from keras.layers import Dense

y = np.array(list(np.arange(1, 6))*1000)
# y = [1, 2, 3, 4, 5, 1, 2, 3, 4, 5, 1, 2, 3 ...]
x = np.arange(0, len(y))
# x = [0, 1, 2, 3, 4, 5, 6, 7, 8...]

Ahora vamos a construir todo un perceptrón multicapa, con varias capas densas, que intente predecir, para un valor de x, su correspondiente y:

modelo = Sequential()
# Un solo dato de entrada (cada valor de la secuencia)
modelo.add(Input(shape=(1,)))
modelo.add(Dense(25, activation='linear', kernel_initializer='uniform'))
modelo.add(Dense(25, activation='linear', kernel_initializer='uniform'))
modelo.add(Dense(25, activation='linear', kernel_initializer='uniform'))
modelo.add(Dense(1, activation='linear', kernel_initializer='uniform'))

Compilamos el modelo y lo entrenamos con el conjunto de datos inicial:

modelo.compile(loss='mae')
modelo.fit(x, y, epochs=100)

Ahora vamos a pedirle que nos prediga cuáles son los siguientes 3 números de la secuencia:

print("Predicción de siguientes números:")
x_test = np.array([len(y), len(y)+1, len(y)+2])
y_pred = modelo.predict(x_test).flatten()
print(y_pred)

Obtendremos como resultado algo parecido a esto:

[2.9656572 2.9656527 2.965648 ]

¿Qué es lo que ha ocurrido? Básicamente hemos planteado un problema de regresión lineal. La red ha distribuido los puntos, ha calculado la recta que mejor se aproxima a ellos y la ha prolongado en el tiempo, permitiendo así calcular los puntos siguientes. El problema es que la recta es una línea horizontal en este caso, que pasa cerca de la media de valores que estamos introduciendo, que es 3.

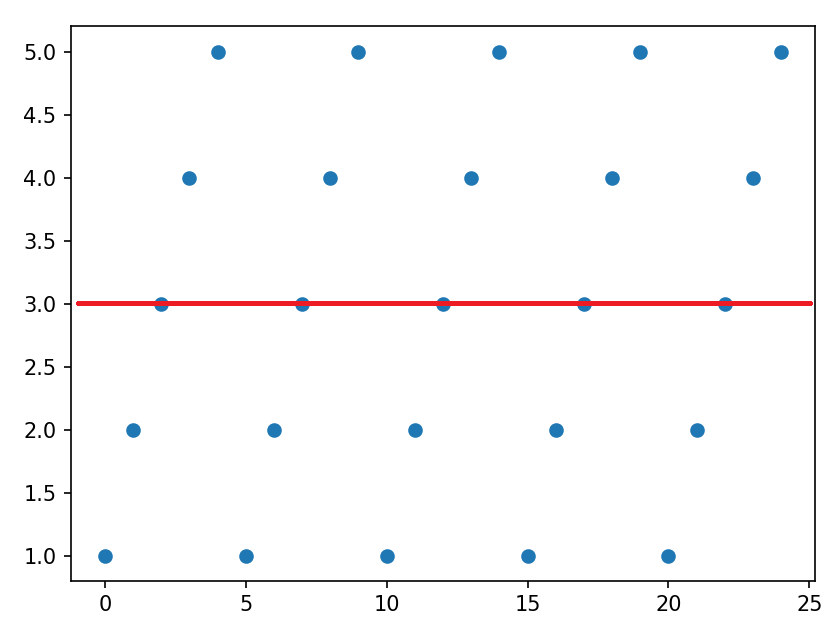
Dicho de otro modo, esta red convencional, por muchas capas y neuronas que pongamos, es incapaz de predecir un valor teniendo en cuenta la secuencia previa de valores que hay. Además, hemos planteado mal el enfoque de entradas y salidas. Intentamos que la red prediga cuál va a ser el n-ésimo elemento de la serie, dados los n valores previos, cuando en realidad deberíamos preguntarle qué número sigue a una secuencia dada como entrada. Por ejemplo, "para la secuencia [2 3 4 5 1 2 3 4], ¿cuál es el siguiente número?". Veremos a continuación cómo podemos reformular el problema.

1.1. Los timesteps¶

Un paso importante en la configuración de redes que deban predecir un valor futuro en una secuencia es la definición de los timesteps. Este parámetro hace referencia a cuántos instantes o pasos atrás necesitamos tener en cuenta, o será capaz de recordar la red. Es un parámetro que puede calcularse de forma empírica, haciendo pruebas con varios valores (1, 10, 20...). La idea es, dado un timestep T tomar el conjunto de entrenamiento e ir haciendo grupos de T valores e intentar predecir con ellos el T+1. Por ejemplo, si T = 10, tomaríamos los 10 primeros valores e intentaríamos predecir el 11, y luego tomaríamos los valores del 2 al 11 e intentaríamos predecir el 12, y así sucesivamente.

El código podría quedar así, partiendo una variable df (dataframe de Pandas) con los datos de entrada ya preparados:

T = 10
df = ... # Preparar dataframe

X_train = []
y_train = []
# Añadimos los T valores correspondientes
# y el valor a predecir
# Ponemos columna 0 suponiendo que el dataframe
# sólo tiene una columna a estudiar
for i in range(T, len(df)):
    X_train.append(df[i-T:i, 0])
    y_train.append(df[i, 0])
# Convertirmos las listas a arrays de NumPy
X_train, y_train = np.array(X_train), np.array(y_train)

Note

El conjunto X_train en el ejemplo anterior es un array bidimensional de datos, donde en cada fila tenemos una secuencia de T valores. En algunos casos podría interesar tener un array tridimensional, donde podamos almacenar en paralelo varias secuencias de un mismo valor, o secuencias de distintos valores para un mismo fenómeno o punto de partida. Podemos usar algo como X_train = np.reshape(X_train.shape[0], X_train.shape[1], N), siendo N el número de capas paralelas que queramos añadir.

1.2. Reformulando el ejemplo anterior¶

Volvamos al ejemplo anterior donde intentamos predecir cuál será el siguiente valor en una secuencia continua de números del 1 al 5. Vamos a intentar resolver el problema ahora usando una red convencional y timesteps.

Comenzamos igual que antes, definiendo la secuencia de valores repetidos 1, 2, 3, 4, 5... En este caso no serán necesarios los valores de x:

import numpy as np
from keras.models import Sequential
from keras.layers import Dense

y = np.array(list(np.arange(1, 6))*1000)

El siguiente paso será configurar los conjuntos de entrada con el correspondiente timestep. Por ejemplo, vamos a tomar un T = 5, que coincide con la secuencia de 5 dígitos que se repite.

T = 5
X_train = []
y_train = []
for i in range(T, len(y)):
    X_train.append(y[i-T:i])
    y_train.append(y[i])
X_train, y_train = np.array(X_train), np.array(y_train)

Así quedarán los vectores que hemos definido:

Elemento	Secuencia (5 números)	Elemento	Resultado
`X_train[0]`	`[1 2 3 4 5]`	`y_train[0]`	`1`
`X_train[1]`	`[2 3 4 5 1]`	`y_train[1]`	`2`
`X_train[2]`	`[3 4 5 1 2]`	`y_train[2]`	`3`
...	...	...	...

Ahora construimos la red. Añadiremos tres capas ocultas de 5 neuronas cada una, por ejemplo, y una capa de salida de una neurona que emitirá cuál es el valor que seguirá a la secuencia de entrada:

modelo = Sequential()
modelo.add(Input(shape=(X_train.shape[1],)))
modelo.add(Dense(5, activation='linear', kernel_initializer='uniform'))
modelo.add(Dense(5, activation='linear', kernel_initializer='uniform'))
modelo.add(Dense(5, activation='linear', kernel_initializer='uniform'))
modelo.add(Dense(1, activation='linear', kernel_initializer='uniform'))

Compilamos y entrenamos la red con los datos de entrada X_train e y_train.

modelo.compile(optimizer='adam', loss='mae')
# Con un número bajo de epochs nos bastará para 
# comprobar los resultados en este caso
modelo.fit(X_train, y_train, epochs=10)

Note

Podemos comprobar cómo, en este caso, la función de pérdida va disminuyendo, mientras que en el ejemplo anterior no bajaba de un cierto valor de loss, cuando ya había ajustado la recta de regresión.

Ahora vamos a pedirle a la red que nos prediga cuál va a ser el siguiente valor dadas unas secuencias de números de entrada (tenemos que respetar el mismo formato de entrada de datos que en el entrenamiento):

print("Predicción de siguientes números:")
x_test = np.array([np.array(list(np.arange(1, 6))), 
    np.array([3, 4, 5, 1, 2]),
    np.array([5, 1, 2, 3, 4])])
y_pred = modelo.predict(x_test).flatten()
print(y_pred)

Como secuencias de prueba le hemos pasado tres distintas:

Una con los números 1, 2, 3, 4, 5 (el siguiente número sería el 1)
Otra con los números 3, 4, 5, 1, 2 (el siguiente número sería el 3)
Otra con los números 5, 1, 2, 3, 4 (el siguiente número sería el 5)

El resultado que obtendremos es muy aproximado al real (mejoraría si añadimos más epochs al entrenamiento):

[0.9957801 2.9836855 5.048282 ]

Como vemos, el incluir el factor tiempo mejora mucho la predicción de resultados basados en secuencias temporales. Sin embargo, el uso de una red neuronal convencional se quedará corto en muchos casos, o se limitará a "memorizar" las secuencias de entrenamiento para saber qué dato va a continuación en cada caso. Necesitamos un paso más para poder predecir mejor el resultado en series temporales. Echemos un vistazo a las redes recurrentes.

2. Fundamentos de las RNR¶

Como decimos, ciertos problemas no pueden resolverse con los datos tomados en un instante determinado. Por ejemplo:

¿Cómo podríamos predecir el valor de una acción en el futuro? Necesitamos conocer la secuencia de valores que ha ido tomando dicha acción a lo largo de los días.
¿Cómo podemos determinar si una reseña o crítica a un restaurante es positiva o negativa? No nos basta con una sola palabra, necesitamos saber la frase entera que se ha escrito, y el orden en que se han indicado las palabras.
¿Cómo podemos predecir qué va a pasar en una película? No basta con el fotograma actual, necesitamos saber la trama que ha ido ocurriendo hasta este momento en la película.

Una red neuronal tradicional no serviría para este tipo de problemas, puesto que su salida únicamente está condicionada por una entrada (un valor, una imagen), pero no tenemos forma de proporcionarle una secuencia de datos y que los tenga todos en cuenta para tomar su decisión final. Para solucionar este problema surgieron las redes neuronales recurrentes. La primera idea fue propuesta por Jordan en 1986, y más tarde, en 1997, Hochreiter y Schmidhuber propusieron las neuronas LSTM que, como veremos, ayudaron a mejorar el funcionamiento general de este tipo de redes.

2.1. Las neuronas recurrentes¶

Las redes neuronales recurrentes están compuestas por neuronas recurrentes. Una neurona recurrente se diferencia de la neurona o perceptrón tradicional en que dispone de un bucle recurrente, que les permiten mantener un estado en el tiempo. Así, la salida en un instante de tiempo t de una neurona (llamemos a esa salida y_t), vendrá dada por la entrada a la neurona en ese instante x_t y la salida en el instante anterior y_t-1. También podemos ver esto como una secuencia de pasos en una neurona, donde cada paso conecta su estado al siguiente paso.

Una red recurrente estará formada por muchas neuronas de este tipo, cada una recibiendo su(s) entrada(s) x y produciendo su(s) salida(s) y.

2.2. Ámbitos de aplicación¶

El hecho de disponer de neuronas recurrentes permite aplicar las RNR en diferentes tipos de problemas:

Uno a uno: serían los problemas convencionales que se pueden resolver con perceptrones multicapa clásicos: a una entrada determinada le corresponde una salida.
Muchos a uno: se reciben muchos datos de entrada secuencialmente para producir una salida. Por ejemplo, a partir de una reseña en un restaurante (secuencia de muchas palabras) concluir si es una reseña positiva o negativa (un único resultado final). Es lo que se denomina análisis de sentimiento.
Uno a muchos: se recibe un único dato de entrada a partir del cual la salida debe constar de una secuencia de datos. Por ejemplo, a partir de una imagen, emitir una descripción de lo que contiene dicha imagen (secuencia de palabras).
Muchos a muchos: se recibe una secuencia de varios datos como entrada y se emite una secuencia de varios datos como salida. Ejemplos típicos son los sistemas de traducción automática (caso 1 del esquema anterior, donde necesitamos algo de contexto previo para empezar a traducir), o los subtítulos automáticos en vídeos (caso 2, donde se subtitula sobre la marcha cada entrada que se recibe).

2.3. El problema del gradiente. Las neuronas LSTM.¶

Como hemos visto, una red neuronal recurrente puede acudir a datos de estados anteriores para ayudar a predecir la salida del instante actual. En ocasiones sólo es necesario un contexto cercano al estado actual para poder deducir la salida. Por ejemplo, si decimos "El perro dice X", podemos concluir analizando tres o cuatro palabras previas que la palabra X debería ser "guau".

Pero en algunas ocasiones hace falta irse más atrás para poder deducir adecuadamente el resultado que se tiene que generar, y esto es un problema para las redes recurrentes ya que, a medida que aumenta la distancia temporal, se diluye más la información que se había recibido. También a la hora de propagar el error cometido desde un instante t, se debe propagar a instantes anteriores.

A medida que el error viaja hacia atrás, o necesitamos acudir a instantes más lejanos en la secuencia, la información de que se dispone sobre esos instantes es más remota, y la medida del error cometido entonces se distorsiona, dependiendo del valor del gradiente. Para valores bajos hará que poco a poco se vaya diluyendo en el tiempo hacia atrás (vanishing gradient, desvanecimiento del gradiente), y para valores altos hará que se vaya agrandando hacia atrás (exploding gradient). Esto constituye un problema grave en el desarrollo de las redes recurrentes ya que, si los estados anteriores están mal calibrados, afectarán a las predicciones futuras de nuevas entradas.

Afortunadamente, en 1997 Hochreiter y Schmidhuber encontraron una solución al problema a través de las neuronas LSTM (Long Short-Term Memory), que permiten dotar a las neuronas no sólo de memoria a corto plazo, sino también a largo plazo. La diferencia principal entre una neurona LSTM y una neurona recurrente es que las primeras incluyen una celda o bucle de memoria. El mecanismo por el que se definen estas neuronas es bastante complejo de explicar, y no profundizaremos mucho en él en este documento. Aquí tenéis un artículo que explica en detalle los mecanismos de las neuronas LSTM, y aquí otro artículo alternativo o complementario.

Básicamente, la idea consiste en añadir un canal adicional c, que atraviesa los estados, y al que se le pueden añadir a través de ciertas válvulas los datos de la información siguiente. De esta manera, modulando las nuevas entradas, se decide qué parte de la información se conserva, y cuál dejamos pasar a los siguientes estados.

Fuente: colah.github.io

Así, las neuronas LSTM incluyen una serie de puertas que permiten controlar la información que entra y sale de la celda de memoria:

Puerta de entrada: controla los valores de entrada que se van a utilizar para actualizar el estado de la memoria. Viene dada por una combinación de funciones sigmoide y tangente hiperbólica. En la figura anterior correspondería a la puerta central de la figura.
Puerta de salida: decide qué parte de la memoria de la celda se usará para el estado siguiente. La función es una combinación de sigmoide y tangente hiperbólica. Corresponde a la puerta derecha en la figura anterior
Puerta de olvido: controla el mantenimiento del contenido de la memoria, y decide cuánta información del estado anterior debe olvidarse. Viene definida por una función sigmoide sobre la entrada y el estado anterior, de modo que si es cercano a 0 la información se olvida y si es cercano a 1 se mantiene. Corresponde a la puerta izquierda en la figura anterior.

En las neuronas recurrentes se tiene una función de activación convencional para producir un nuevo resultado, y una función de activación recurrente para modular la salida que retroalimentará a la neurona. La función de activación convencional normalmente es una tangente hiperbólica (tanh), y la función de activación recurrente suele ser una sigmoide.

2.4. Recurrencia bidireccional¶

En algunas ocasiones interesa no sólo el contexto previo, sino el contexto posterior, a la hora de tomar una decisión o emitir un resultado acertado. Por ejemplo, si estamos analizando si una reseña es positiva o negativa, puede que al principio pueda parecer negativa si identificamos alguna palabra suelta ("horrible", "desastre"...). Pero, si vamos mas allá, puede que la propia reseña luego matice ese resultado y tengamos que descartar esa palabra.

Para facilitar esto, las neuronas recurrentes pueden tener dos conexiones, en direcciones opuestas:

3. Redes recurrentes con Keras/TensorFlow¶

Veamos ahora cómo se definen redes recurrentes en Keras/TensorFlow.

3.1. Elementos necesarios y construcción de la red¶

Para construir redes recurrentes necesitaremos algunos viejos conocidos de otros documentos, como la clase Sequential del paquete keras.models, o las capas Input, Dense y Dropout de keras.layers. A esto último añadiremos ahora la clase LSTM, también de keras.layers, para definir las capas recurrentes.

Respecto al constructor de LSTM, recibe estos parámetros:

units: número de neuronas recurrentes en la capa. Podemos ajustarlo de forma experimental, aunque en general interesarán valores altos para añadir complejidad a la red y que sea capaz de aprender secuencias más o menos complejas. También podemos variar el número de unidades en las distintas capas recurrentes.
return_sequences: booleano que indica si queremos ir apilando los valores de retorno. Será True si queremos conectar esta capa recurrente con otra posterior, y normalmente se pone a False en la última (salvo algunos casos de muchas salidas).
input_shape: en el caso de omitir la capa de entrada, en este parámetro indicamos el número de conexiones de entrada de la red. Este parámetro sólo se ajusta en la primera capa LSTM, ya que el resto tomará automáticamente el tamaño de las capas anteriores. También podemos omitir este parámetro si especificamos una capa Input inicial, como en las redes multicapa convencionales.
Además, existen otros parámetros que permiten definir, por ejemplo, las funciones de activación. En el caso de capas LSTM se pueden configurar dos funciones de activación: una para generar el valor para la capa siguiente (normalmente es una función tanh), y otra para la propia recurrencia de la capa (normalmente es una función sigmoide). Ambos parámetros vienen inicializados con sus funciones por defecto.

Aquí vemos cómo construir una red con varias capas recurrentes (LSTM), incluyendo dropout entre ellas.

modelo = Sequential()

# Capa de entrada
modelo.add(Input((X_train.shape[1], 1)))

# Capas LSTM
modelo.add(LSTM(units=50, return_sequences=True))
modelo.add(Dropout(0.2))
modelo.add(LSTM(units=50, return_sequences=True))
modelo.add(Dropout(0.2))
modelo.add(LSTM(units=50, return_sequences=True))
modelo.add(Dropout(0.2))

# Capa final LSTM (return_sequences = False)
modelo.add(LSTM(units=50))
modelo.add(Dropout(0.2))

# Capa de salida (por ejemplo, con 1 neurona)
modelo.add(Dense(units=1))

Sobre el formato de datos

Como ya podemos intuir, para entrenar las redes recurrentes tendremos que proporcionar los datos en secuencias. Así, por ejemplo, para una red muchos a uno, cada muestra de entrenamiento constará de una secuencia de entrada y de una etiqueta o valor de salida. El conjunto de datos de entrada será un array tridimensional donde:

En la primera dimensión indicaremos el número de ejemplos que pasaremos a la red
En la segunda dimensión indicaremos la longitud de cada secuencia de datos, que típicamente se suele asociar a X_train.shape[1].
En la tercera dimensión las características de cada dato (normalmente cada dato consta de un solo valor, pero podría tener más)

En el caso de la salida se tendrán dos dimensiones, donde la primera indicará el número de resultados producidos, y la segunda el valor de cada resultado (nuevamente, en el caso de una red muchos a uno).

3.2. Compilación, entrenamiento y predicción¶

Para compilar la red, usaremos el método compile, especificando el optimizador y la función de pérdida, como en anteriores ejemplos.

modelo.compile(optimizer='adam', loss='mse')

Para entrenar a la red, usamos el método fit indicando los conjuntos de entrenamiento X e y:

modelo.fit(X_train, y_train, epochs=100, batch_size=32)

A la hora de predecir, usamos el método predict indicándole el conjunto de datos de entrada, que deberán tener una forma similar a los que hemos utilizado para entrenar.

predicciones = modelo.predict(X_test)

3.3. Un ejemplo¶

Volvamos a nuestro ejemplo inicial de predecir una secuencia de valores continuos del 1 al 5. Vamos a reemplazar el perceptrón multicapa del intento anterior por una red recurrente. Los primeros y últimos pasos no cambian, sólo cambiaremos el modelo de red por este otro, con tres capas recurrentes:

import numpy as np
from keras.models import Sequential
from keras.layers import Dense, Dropout, LSTM

... # El código para configurar X_train e y_train no cambia

modelo = Sequential()

modelo.add(Input((X_train.shape[1], 1)))

modelo.add(LSTM(units=5, return_sequences=True))
modelo.add(Dropout(0.2))
modelo.add(LSTM(units=5, return_sequences=True))
modelo.add(Dropout(0.2))
modelo.add(LSTM(units=5))
modelo.add(Dropout(0.2))

modelo.add(Dense(units=1))

... # El código para compilar, entrenar y probar la red no cambia

Notar que en este caso la entrada es una tupla con dos valores a la primera capa recurrente la definimos con input_shape, ya que en el caso de redes recurrentes necesitamos definir una tupla con el tamaño del conjunto de valores de entrada (5, en nuestro caso), y cuántos conjuntos de valores se pasarán a la vez como entrada (1).

Los resultados obtenidos en este caso son similares a los de la red multicapa, aunque ligeramente peores:

[0.9254465 2.7648053 4.4466567]

El motivo del empeoramiento es que, en redes recurrentes, normalmente hacen falta capas más densas para retener la información previa y procesarla correctamente; subiendo el número de neuronas a 20 o 30 en las capas ocultas mejoramos el resultado. Podríamos pensar que esto es un retroceso con respecto a lo que ya sabemos... Sin embargo, como veremos en ejemplos posteriores, el uso de redes recurrentes LSTM supone una mejora importante en la predicción de valores en secuencias temporales más complejas

Puedes descargar aquí el código fuente de los distintos ejemplos que hemos realizado sobre este problema de la secuencia de valores de 1 a 5: una red MLP sencilla (v1), una red MLP con timesteps (v2) y esta última versión con capas LSTM (v3).

3.4. Ajuste de hiperparámetros en una RNR¶

A la hora de mejorar el comportamiento de una red neuronal recurrente, existen algunos hiperparámetros que podemos ajustar, además de los habituales en una red neuronal convencional:

Por un lado, podemos intentar aumentar el conjunto de datos de entrada de que disponemos, para tener más información con la que entrenar a la red
También podemos variar el tamaño del timestep, para ver qué rango de valores optimiza los resultados obtenidos
En el conjunto de datos de entrada podemos añadir otras secuencias en paralelo. Por ejemplo, si estamos analizando el valor de una acción, tomaríamos la secuencia de valores de dicha acción en el tiempo como entrada. Pero, si tenemos conocimiento de que otras acciones pueden afectar al valor de la acción que estamos estudiando, podríamos añadir al dataset de entrada otras secuencias con los valores de esas otras acciones.
Agregar más capas LSTM y/o más unidades en cada capa, para dotar a la red de mayor capacidad de análisis.

Ejercicio 1

Descarga este dataset sobre valores de una acción a lo largo de varios años. Utiliza este documento Google Colab para cargar el dataset y predecir el valor de la acción durante 2017, tomando como base los valores en los años previos. Crea para ello una RNR con los parámetros que se te indican en el documento Colab.

Ejercicio 2

Sobre el ejercicio anterior, evalúa el funcionamiento de otros modelos de red, como estos:

5 capas recurrentes de 80 neuronas cada una, optimizador adam, T = 90, 50 epochs
4 capas recurrentes de 80 neuronas cada una, optimizador sgd, T = 30, 100 epochs

Determina qué modelo ha obtenido mejores resultados (contando también con la RNR del ejercicio anterior)

3.5. Redes recurrentes bidireccionales¶

Keras dispone de una capa especial llamada Bidirectional, en el paquete keras.layers, que nos permite crear capas recurrentes con conexión bidireccional (hacia adelante y hacia atrás). Se utilizan como un wrapper que encapsula la capa LSTM que queremos convertir en bidireccional. Por ejemplo:

modelo = Sequential()

...
modelo.add(Bidirectional(LSTM(units=50, return_sequences=True)))
...
modelo.add(Dense(units=1))

Ejercicio 3

Partiendo del Ejercicio 1 anterior, prueba otro modelo diferente transformando la red recurrente inicial en una bidireccional. Haz todas las capas LSTM bidireccionales salvo la primera, que toma los datos de entrada. Compara los resultados (y el tiempo de entrenamiento) de esta red con la original.