Q-learning¶

En este documento analizaremos la técnica de Q-learning, una técnica de aprendizaje por refuerzo que resuelve problemas de tomas de decisiones que cumplan una serie de requisitos que explicaremos a continuación.

1. Introducción¶

Q-learning es una estrategia de aprendizaje por refuerzo que trabaja en un entorno determinado, donde nos podemos encontrar en un número finito de estados (inputs) con un número finito de acciones a realizar en cada estado. Por ejemplo, elegir qué camino tomar en un laberinto para llegar a una salida; existe un número finito de estados (cada una de las casillas del laberinto) y un número finito de acciones a realizar desde cada estado (a qué otras casillas podemos llegar en el siguiente movimiento).

Cada vez que iniciemos una acción a desde un estado e obtendremos una recompensa R. Igual que ocurre con otras estrategias similares, se tratará de maximizar esta recompensa pero, esta vez, aplicando una serie de fórmulas y principios particulares que analizaremos a continuación.

2. Un ejemplo introductorio¶

Supongamos que queremos mover un robot por un almacén, para ir de una ubicación a otra. Cada una de las posibles ubicaciones del almacén la identificamos con una letra, y definimos también los muros que separan las distintas ubicaciones, por los que el robot no podrá pasar.

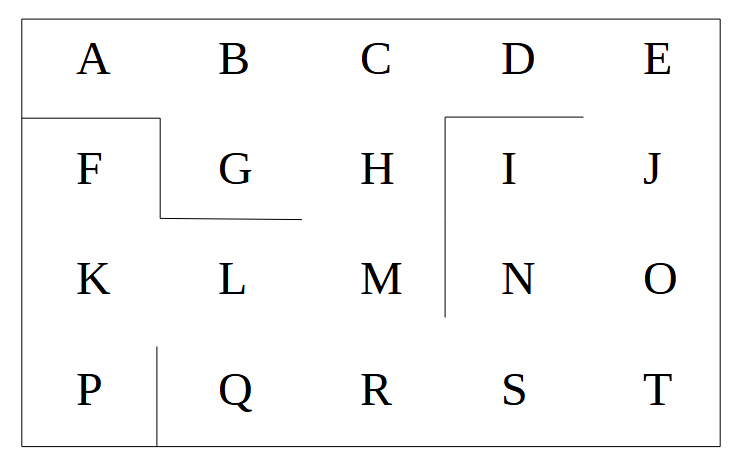
Supongamos, por concretar más, que queremos dirigir a nuestro robot desde el punto B al punto I. Tendremos que hacerlo de forma que sepa elegir el camino más corto (en verde en la imagen inferior). Es decir, que el camino más corto le aporte mayor recompensa que el resto de opciones.

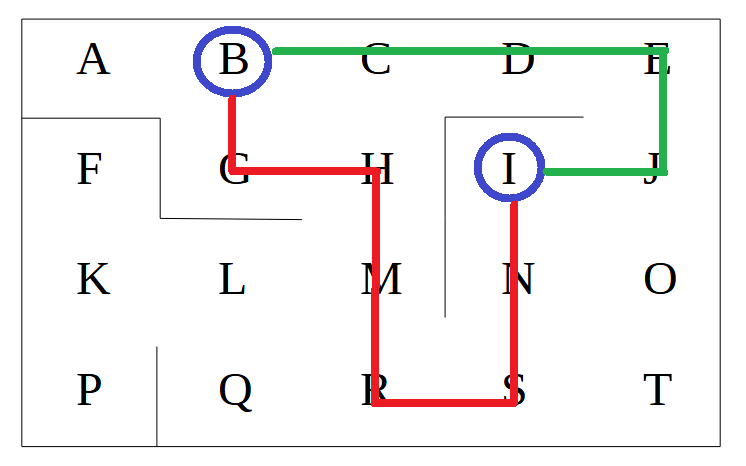
2.1. Definiendo el entorno¶

Comenzaremos definiendo el entorno: estados o inputs del problema, acciones a realizar y recompensas a obtener.

El estado o input en un instante específico será la letra o casilla en que nos encontramos en el mapa (en el ejemplo anterior, de la A a la T). Codificaremos cada letra con un código numérico: A = 0, B = 1... T = 19. Observa que tenemos un número finito de estados, como corresponde a una de las premisas de Q-learning.
La acción será a qué casilla nos queremos mover. Así, el conjunto (nuevamente finito) de posibles acciones serán los códigos de las casillas: del 0 al 19 en el ejemplo anterior.
La recompensa debe determinar qué puntuación nos llevaremos cuando, a partir de un estado e, emprendemos la acción a (R(e,a)). Como tenemos un número finito de estados y de acciones, la forma simple de definir esto es con una matriz bidimensional, donde al estado (fila) le corresponde la recompensa (columna). Asignaremos un 0 a las transiciones imposibles. Por ejemplo, si desde el estado A no podemos acceder directamente al estado D, la recompensa R(A,D) será 0, para evitar que se tome esa decisión. Inicialmente asignaremos una recompensa de 1 a las acciones que sí se pueden realizar (casillas conectadas). Obtendremos una matriz como ésta:

  A B C D E F G H I J K L M N O P Q R S T
A 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
B 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
C 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
D 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
E 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0
F 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
G 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
H 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
I 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0
J 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0
K 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0
L 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 0 0
M 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0
N 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0
O 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 1
P 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
Q 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0
R 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0
S 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1
T 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0

¿Cómo podemos reforzar que el sistema (robot) se dirija a un punto concreto Y de la lista? Tenemos que asignar una recompensa más alta a ese punto (por ejemplo, 1000), en el array de recompensas. Si, por ejemplo, el objetivo es llegar al punto I, como en nuestro ejemplo, todos los valores a 1 de la columna I se pondrían a 1000.

Vamos a definir en Python este entorno inicial para nuestro problema: crearemos un diccionario donde asociaremos cada letra con su código numérico:

import numpy as np

def generar_estados():
    estados = {
        'A': 0,
        'B': 1,
        'C': 2,
        'D': 3,
        'E': 4,
        'F': 5,
        'G': 6,
        'H': 7,
        'I': 8,
        'J': 9,
        'K': 10,
        'L': 11,
        'M': 12,
        'N': 13,
        'O': 14,
        'P': 15,
        'Q': 16,
        'R': 17,
        'S': 18,
        'T': 19
    }
    return estados

Hemos incorporado la librería NumPy porque nos será de utilidad para definir los distintos vectores y matrices, y realizar algunos cálculos. Definiremos ahora las acciones, como una secuencia de códigos equivalentes a las letras anteriores. La acción 0 significará ir a la casilla A, la acción 1 ir a la casilla B, etc.

def generar_acciones(tamano):
    return np.arange(0, tamano)

También crearemos una tabla bidimensional con las recompensas por ir de un estado a otro, según el ejemplo anterior:

def generar_recompensas():
    return np.array([
        [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0]
    ])

Nota

Podríamos poner a un valor alto (1000, por ejemplo) los unos de la columna I. Esto lo dejaremos pendiente para un ejercicio posterior.

En nuestro programa principal cargamos los códigos, las acciones y el mapa. Acciones habrá tantas como códigos (estados) tenga nuestro problema.

estados = generar_estados()
acciones = generar_acciones(len(codigos))
recompensas = generar_recompensas()

2.2. El valor Q¶

El valor Q (Q-value) asociado a un estado e y una acción a indica lo bueno que es para nuestro propósito emprender la acción a desde el estado e. Se representa como Q(e, a), y es un valor numérico real. Inicialmente, todos estos valores Q se ponen a 0, porque de entrada no sabemos lo bueno o malo que es tomar cada acción desde cada estado.

def inicializar_valores_q(filas, columnas):
    return np.zeros([filas, columnas])

# main
estados = generar_estados()
acciones = generar_acciones(len(estados))
recompensas = generar_recompensas()
valores_q = inicializar_valores_q(recompensas.shape[0], recompensas.shape[1])

Vemos que creamos una matriz Q del mismo tamaño que la matriz de recompensas. En cada casilla Q(e, a) tendremos el valor Q actual que se obtiene eligiendo la acción a desde el estado e. Estos valores Q se van a ir actualizando en sucesivas iteraciones, a medida que vayamos calculando cuál es el mejor camino. Para actualizar el valor debemos hacer uso del siguiente concepto: la diferencia temporal.

2.3. La diferencia temporal¶

Supongamos que estamos en un estado e en una iteración específica t (lo representamos como e_t), y emprendemos en ese instante la acción a (a_t). Esto nos va a proporcionar la recompensa R(e_t, a_t), y nos va a llevar al estado e_t+1.

La diferencia temporal en un instante t (indicada como TD(e_t, a_t)) es la diferencia entre el valor Q de ese estado y acción en ese instante (Q(e_t, a_t)), y la recompensa que obtenemos en ese estado y acción más el mejor valor Q de los posibles estados a los que podemos ir:

TD_t(e_t, a_t) = R(e_t, a_t) + γ · max(Q(e_t+1, a)) - Q(e_t, a_t)

donde γ es un factor de corrección, un número real entre 0 y 1. Cuanto mayor sea, más importancia o peso se le da a los valores de Q circundantes. Dicho de otro modo, un valor cercano a 0 dará más peso a las recompensas inmediatas, y un valor cercano a 1 premiará también buscar valores altos a largo plazo (en nuestro caso, llegar a casillas cercanas valiosas).

Por ejemplo, supongamos la siguiente situación en una tabla de valores Q hipotética para nuestro ejemplo:

  A B C D E F G H I J K L M N O P Q R S T
A 0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
B 2 0 5 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0
C 0 2 0 10 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
D 0 0 2 0 19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
...

Supongamos que estamos en el estado B (fila 2), y elegimos pasar al estado C (columna 3). El valor Q actual de esa casilla es 5. Calcularíamos la diferencia temporal de este modo:

Primero obtenemos la recompensa R de ir de B a C. Según la tabla de recompensas anterior es 1.
Buscamos en la tabla de valores Q para el estado C (fila 3) cuál es el mayor valor. En este caso tenemos el valor 10, correspondiente a ir al estado D. Multiplicamos este máximo valor por un factor de corrección γ. Por ejemplo podemos suponer que γ = 0.7, con lo que obtendremos 7 como resultado. Si tuviéramos un coeficiente γ pequeño este valor sería cercano a 0, y apenas sumaríamos por los valores Q circundantes.
Sumamos los dos datos anteriores (recompensa y máximo valor de Q multiplicado por γ) y le restamos el valor de Q actual: 1 + 7 - 5 = TD = 3

Esta diferencia temporal representa lo bien que nuestra IA va a aprender. Como inicialmente los valores Q se ponen a cero, la IA buscará obtener buenas recompensas R(e, a), para obtener con ellas buenas diferencias temporales. Si obtenemos una buena recompensa, el valor Q de nuestro estado actual para la acción emprendida aumentará, de forma que la IA recordará cómo llegó a obtener una buena recompensa desde ese estado. Así, en futuras iteraciones la IA ya no sólo va a buscar obtener buenas recompensas, sino buscar valores Q altos, que le indicarán que va en camino de la recompensa máxima. Llegará un momento en que la IA tendrá disponible la secuencia de valores Q que le lleven a la recompensa máxima.

2.4. Actualización de valores Q: la ecuación de Bellman¶

Nos falta una pata en esta mesa que estamos construyendo: hemos visto qué son los valores Q, y cómo calcular la diferencia temporal para saber qué acciones nos producen mejores resultados desde cada estado. Pero necesitamos actualizar los valores Q para que las siguientes veces que pasemos por un estado ya sepamos cuál es la acción más recomendable.

Aquí entra en juego la ecuación de Bellman, llamada así en honor a su creador Richard Bellman, uno de los pioneros en el campo del aprendizaje por refuerzo. Según esta ecuación, el valor Q en un instante t determinado (Q_t(e_t, a_t)) será igual al valor Q en el instante anterior (Q_t-1(e_t, a_t)) más la diferencia temporal en ese instante, multiplicada por un factor de corrección α entre 0 y 1:

Q_t(e_t, a_t) = Q_t-1(e_t, a_t) + α · TD_t(e_t, a_t)

Retomando el ejemplo anterior donde habíamos obtenido un TD = 3, suponiendo un α = 0.8, tendríamos que el nuevo valor de Q para el estado B con la acción C sería 5 + 0.83 = 7.4*.

Valores pequeños de α harán que el aprendizaje sea más lento (los incrementos de Q serán más pequeños), y valores altos harán que el aprendizaje vaya más rápido.

2.5. Aplicando el algoritmo¶

Aplicaremos un proceso iterativo (N iteraciones, siendo N ajustable según el proceso), con estos pasos en cada iteración t:

Elegir un estado e_t al azar
Desde ese estado, realizar una acción a_t aleatoria tal que R(e_t, a_t) > 0 (es decir, elegir una acción válida que lleve a otro estado, en nuestro caso)
Alcanzamos el siguiente estado e_t+1 y obtenemos la recompensa R(e_t, a_t)
Calculamos la diferencia temporal TD_t(e_t, a_t) = R(e_t, a_t) + γ · max(Q(e_t+1, a)) - Q(e_t, a_t)
Actualizamos el valor Q usando la ecuación de Bellman: Q_t(e_t, a_t) = Q_t-1(e_t, a_t) + α · TD_t(e_t, a_t)

El objetivo será construir una IA que devuelva el camino más corto entre dos ubicaciones X e Y cualesquiera del mapa anterior.

Definimos ahora nuestro algoritmo iterativo sobre N = 1000 repeticiones. Definimos también constantes para los coeficientes γ y α por ejemplo:

N = 1000
gamma = 0.75
alpha = 0.9

for i in range (N):
    # Algoritmo

El algoritmo en sí puede quedar como sigue, uniendo las piezas de los pasos indicados antes:

Elegir un estado e_t al azar

estado_actual = np.random.randint(0, len(estados))

Desde ese estado, realizar una acción a_t aleatoria tal que R(e_t, a_t) > 0 (es decir, elegir una acción que lleve a otro estado, en nuestro caso)

acciones_validas = []
for j in range(len(estados)):
    if recompensas[estado_actual,j] > 0:
        acciones_validas.append(j)

Alcanzamos el siguiente estado e_t+1 y obtenemos la recompensa R(e_t, a_t)

siguiente_estado = np.random.choice(acciones_validas)

Calculamos la diferencia temporal TD_t(e_t, a_t) = R(e_t, a_t) + γ · max(Q(e_t+1, a)) - Q(e_t, a_t)

TD = recompensas[estado_actual, siguiente_estado] + \
    gamma * valores_q[siguiente_estado, np.argmax(valores_q[siguiente_estado,])] - \
    valores_q[estado_actual, siguiente_estado]

Actualizamos el valor Q usando la ecuación de Bellman: Q_t(e_t, a_t) = Q_t-1(e_t, a_t) + α · TD_t(e_t, a_t)

valores_q[estado_actual, siguiente_estado] += alpha * TD

Ejercicio 1

Crea un programa almacen_q_learning.py con los pasos indicados hasta este momento. Define el código para optimizar el recorrido desde el punto B hasta el punto I, e imprime la matriz de valores Q resultantes cada 200 iteraciones, para ver cómo cambian.

Nota

Recuerda que, para dirigir al robot al objetivo (punto I) debemos dar una recompensa mayor en la columna I.

Solución Ejercicio 1

Aquí puedes ver un vídeo con la solución paso a paso del ejercicio.

Ejercicio 2

Partiendo del Ejercicio 1, compara las matrices Q finales que se obtienen con 1000 iteraciones variando los coeficientes del algoritmo:

γ = 0.75 y α = 0.9 como en el ejemplo inicial
Dejando los dos valores a 0.1
γ = 0.7 y α = 0.1

2.6. Aplicando inferencia¶

Ahora que ya tenemos el algoritmo construido, queda saberlo aplicar: ya tenemos la matriz de valores Q construida para alcanzar un objetivo Y determinado. ¿Cómo podemos "preguntar" cuál es la ruta más adecuada para ir desde un punto X hasta ese objetivo?

Definiremos una función ruta, a la que le pasaremos un estado inicial y uno final:

def ruta(letra_inicial, letra_final):
    solucion = [letra_inicial]
    estado_actual = estados[letra_inicial]
    estado_final = estados[letra_final]
    while(estado_actual != estado_final):
        siguiente_estado = np.argmax(valores_q[estado_actual,])
        # Convertimos el código del siguiente estado en su letra
        # Obtenemos la clave del diccionario a partir del valor
        siguiente_letra = \
            [letra for letra, estado in estados.items() \
             if estado == siguiente_estado][0]
        solucion.append(siguiente_letra)
        estado_actual = estados[siguiente_letra]
    return solucion

Ejercicio 3

Completa el ejercicio anterior preguntando la ruta para ir del punto B al punto I.

Ejercicio 4

Modulariza adecuadamente el código para poder ir de cualquier punto a cualquier punto: al principio le preguntaremos al usuario el punto origen y destino (letras), y construiremos con ello el array de valores Q correspondiente, para luego mostrar la respuesta.

3. Aplicaciones del Q-learning¶

El algoritmo de Q-learning se puede aplicar a multitud de ámbitos:

Ya hemos visto que es especialmente apropiado para tareas de robótica y control de sistemas, optimizando el movimiento de robots en entornos controlados.
También podemos aplicarlo en juegos y estrategia, para aprender a jugar a ciertos juegos con estados y acciones finitas, como el ajedrez o el Go.
En el ámbito de las finanzas, podemos emplearlo para tomar decisiones sobre la compra/venta/mantenimiento de activos financieros, buscando maximixar el beneficio obtenido
En el campo de la salud podemos utilizarlo, por ejemplo, para estimar las dosis adecuadas de medicación en pacientes, en base a sus síntomas y datos analíticos en cada momento.

Ejercicio 5

Queremos desarrollar un asistente virtual de compras que recomiende a los usuarios otros productos que les puedan interesar. Vamos a aplicar la estrategia de Q-learning para determinar cuál es el producto más adecuado que recomendar a un usuario en base a las compras previas que se hayan realizado. Utilizaremos como catálogo de productos este archivo CSV.

Para definir las recompensas, utilizaremos una matriz bidimensional N x N, siendo N el total de productos del catálogo. En cada casilla [i, j] iremos incrementando en 1 la recompensa cada vez que el usuario con el producto i en su historial de compras elija también el producto j. Inicialmente esta tabla de recompensas estará rellena con ceros. La tabla de valores Q, también inicialmente a ceros, será del mismo tamaño. Al finalizar el programa guardaremos ambas tablas en dos ficheros recompensas.txt y valores_q.txt, para recuperarlas en la siguiente sesión.

Elabora un programa que, repetidamente:

Le pida al usuario que elija un producto del catálogo para comprar (introduciendo su id o código)
Incremente la recompensa del producto elegido, en base a los productos previamente comprados por el usuario
Recalcule el valor Q de haber elegido ese producto con su historial previo de compras
Muestre al usuario un producto del catálogo como recomendación

Cuando el usuario introduzca un código 0 de producto, finalizará el programa y guardará las tablas actualizadas para la siguiente vez

Solución Ejercicio 5

Aquí puedes ver un vídeo con la solución paso a paso del ejercicio.