Ejemplos de tratamiento de datos

Cuando necesitamos desarrollar una aplicación en el mundo real normalmente los datos que necesitamos para nuestra aplicación no están directamente disponibles en un formato adecuado. A menudo, incluso, estos datos provienen de diferentes fuentes de datos. En cualquier caso, debemos disponer de algún mecanismo para recuperar esos datos, limpiar las partes que no nos interesen y dejar el resto estructurado en un formato adecuado para nuestro programa. Además, conviene conocer la composición de estos datos y sus características relevantes. Este proceso general se suele componer al menos de tres etapas, que no necesariamente se deben realizar en el orden que aquí se indica.

• Limpieza de datos (data cleaning): consiste en procesar los datos para eliminar las partes que no interesen y dar un formato adecuado a las que sí. Por ejemplo, gestionar los valores nulos que pueda haber, o los valores anómalos, ver el tipo de dato adecuado para cada columna, etc.
• Ingeniería de datos (data engineering): consiste en generar nuevos datos a partir de los que ya existen. Aquí entran aspectos como la selección de características relevantes, la conversión de variables categóricas en numéricas, o el escalado de los datos para que todos tengan el mismo peso o importancia.
• Análisis exploratorio de datos (EDA, Exploratory Data Analysis), que consiste en analizar los datos de que disponemos buscando patrones o información relevante: medias, modas, tendencias, distribución de valores, etc. Para ello se suele hacer uso de las representaciones gráficas que ya hemos explicado en este documento y que también se pueden resumir en este otro.

La calidad o precisión de las decisiones que pueda tomar un programa dependen en gran parte de la calidad de los datos que le proporcionamos de entrada. En general, podemos considerar que los datos de que disponemos son de calidad si se ajustan a las operaciones que sobre ellos se realizan. Dicho de otro modo, no hay un estándar para medir esa calidad de los datos y, en general, dependerá de su adecuación al programa en cuestión.

En este documento veremos algunos ejemplos de técnicas de tratamiento y análisis de datos que podemos aplicar en nuestros desarrollos, siempre como paso previo a la ingesta de datos por parte de la aplicación. Hay que tener en cuenta que, en muchas ocasiones, este proceso de tratamiento y limpieza de datos puede llevar mucho más tiempo que lo que supone el desarrollo del modelo en sí.

1. Presentación del caso de prueba

Tomaremos como base este dataset que contiene información sobre datos de salud de distintos pacientes: género, edad, peso, colesterol... Pretendemos desarrollar un modelo que prediga la presión sanguínea alta de un paciente (también llamada presión sistólica, almacenada en la columna ap_hi) a partir del resto de información. Como veremos, el documento CSV tiene muchas características, pero algunas de ellas van a resultar irrelevantes para determinar el valor objetivo, y otras que sí van a ser relevantes tendrán datos incompletos que tendremos que gestionar.

Podemos crear un cuaderno en Google Colab y cargar el CSV para ir probando en él los pasos que explicaremos a continuación.

1.1. Carga de librerías

Comenzaremos importando las librerías necesarias para nuestro proyecto:

• NumPy (alias np)
• Matplotlib (módulo pyplot con alias plt)
• Pandas (alias pd)
• Seaborn (alias sns)

Además, de la librería sklearn incorporaremos algunos módulos que nos van a resultar de utilidad para ciertas tareas puntuales:

• Módulo mean_absolute_error de sklearn.metrics, que usaremos para medir cómo de buenos o malos son los cálculos que haremos
• Módulo train_test_split de sklearn.model_selection para poder definir conjuntos de entrenamiento y test en nuestros datos
• Clase DecisionTreeRegressor de sklearn.tree para aplicar un árbol de decisión al final, para hacer una estimación más o menos aproximada de algún parámetro del CSV en cuestión. En nuestro caso, estimaremos la presión sanguínea alta o sistólica (columna ap_hi).

# Importar librerías
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

from sklearn.metrics import mean_absolute_error
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor

1.2. Carga del CSV y presentación inicial de los datos relevantes

A continuación, cargaremos los datos del archivo CSV, mostraremos su estructura en pantalla y haremos un primer análisis del dato objetivo (columna ap_hi, presión sanguínea alta). Deberás subir el archivo CSV proporcionado a tu espacio de trabajo en Colab.

# Cargar datos de CSV en variable "datos"
datos = pd.read_csv('datos_salud2.csv')
# Guardarnos en una variable "valor_objetivo" el nombre de columna objetivo "ap_hi"
valor_objetivo = 'ap_hi'

# Mostrar 5 primeras filas
print(datos.head())

# Mostrar tamaño del dataset (filas y columnas)
print(datos.shape)

# Mostrar información relevante de columna 'ap_hi', con su método 'describe'
print(datos[valor_objetivo].describe())

Como podemos observar, disponemos de 70.000 registros, donde el valor máximo es 16020, y el mínimo es -150, siendo el promedio 128.82 aproximadamente. Algunos de estos valores son muy anómalos, ya que una presión de 16020 es totalmente excesiva, y no se pueden tener presiones sanguíneas negativas. Más adelante veremos cómo gestionar estos valores.

2. Limpieza de datos (data cleaning)

Comenzaremos por el proceso de limpieza de datos, que consistirá fundamentalmente en detectar y corregir los valores nulos, las anomalías, y estudiar el tipo de dato más adecuado para cada columna.

2.1. Gestión de valores nulos (missing values)

En algunas ocasiones es posible que algún campo o columna de nuestros datos tenga algún valor nulo o faltante. Esto supone una pérdida de información, que se puede manifestar de distintas formas. Por ejemplo, si nos falta un valor numérico normalmente éste aparece como NaN (Not a Number) una sintaxis especial para identificar datos que se suponen numéricos pero no lo son. En otros casos podemos encontrarnos con un valor NA (Not Available) cuando ese dato en concreto no está disponible.

Por ejemplo, consideremos el siguiente listado de datos personales, donde falta la edad de una persona y el peso de otra:

Nombre	Edad	Peso
Juan	70	75
Ana	NaN	70
Mario	30	NaN
Laura	26	67

Dependiendo del problema, podemos optar por descartar la fila con valores omitidos, o por intentar reemplazar el valor omitido por otro simulado que no sea discordante con el resto, como por ejemplo la media, mediana o moda.

2.1.1. Detección o conteo de valores nulos

La función isnull obtiene si una determinada casilla tiene o no valor. Podemos combinarla con la función sum para saber cuántas casillas vacías tenemos. Podemos construir un ejemplo como el anterior y ver cuántas casillas nulas hay:

import numpy as np
import pandas as pd

datosIniciales = {'Nombre': ['Juan', 'Ana', 'Mario', 'Laura'], 
    'Edad': [70, np.NaN, 30, 26], 
    'Peso': [75, 70, np.NaN, 67]}
datos = pd.DataFrame(datosIniciales)

print("Número de casillas nulas:")
print(datos.isnull().sum())
# Dirá que la columna "Nombre" no tiene valores perdidos
# y la columna "Edad" y "Peso" tienen un valor perdido cada una

Podríamos obtener, por ejemplo, todas las filas de un data frame que tengan nula una determinada casilla:

nulos_edad = datos[datos['Edad'].isnull()]

El siguiente fragmento de código construye una tabla donde, para cada columna, muestra el porcentaje de casillas nulas que tiene respecto al total de filas:

valores_nulos = datos.isnull().sum().sort_values(ascending=False)
# Añadimos "reset_index" para numerar las filas resultantes
ratio_nulos = (valores_nulos / len(datos)).reset_index()
ratio_nulos.columns = ['Caracteristica', 'RatioNulos']
ratio_nulos

2.1.2. Opciones ante la presencia de valores nulos

Si detectamos la presencia de valores nulos en una columna X, básicamente tenemos dos alternativas:

• Una consiste en reemplazar el valor nulo por un valor representativo, que puede ser por ejemplo la media o mediana de valores de la columna (en el caso de valores numéricos) o la moda (el valor que más se repite, útil para valores categóricos). También hay otras opciones, como reemplazar por el valor máximo o el mínimo de la columna. Es lo que se conoce como imputación de valores. Usaremos en cualquier caso el método fillna sobre la columna en cuestión, indicando el valor de reemplazo.

# Reemplazo por ceros
datos['X'].fillna(0, inplace=True)

# Reemplazo por la media
datos['X'].fillna(datos['X'].mean(), inplace=True)

# Reemplazo por la mediana
datos['X'].fillna(datos['X'].median(), inplace=True)

# Reemplazo por la moda (devuelve un array con las ocurrencias mayores)
datos['X'].fillna(datos['X'].mode()[0], inplace=True)

• Otra consiste en eliminar las filas o registros que contengan un valor nulo en esa columna. No es aconsejable en algunos casos porque pueden suponer mucha pérdida de información pero, si se opta por esta opción, podemos utilizar la función dropna de Pandas. Esta función altera el contenido de la colección sobre la que se aplica (además, debemos especificar el parámetro inplace=True, habitual en Pandas para actualizar la colección original).

# Borrar filas con algún campo nulo
datos.dropna(inplace=True)

# Borrar filas que tengan en la columna "X" un valor nulo
datos.dropna(subset=['X'], inplace=True)

2.1.3. Aplicación al ejemplo

En lo que respecta a nuestro ejemplo, vamos a mostrar el porcentaje de nulos que hay en cada columna, usando el código anterior:

valores_nulos = datos.isnull().sum().sort_values(ascending=False)
# Añadimos "reset_index" para numerar las filas resultantes
ratio_nulos = (valores_nulos / len(datos)).reset_index()
ratio_nulos.columns = ['Caracteristica', 'RatioNulos']
ratio_nulos

Vemos que las columnas con nulos son age, gender y cardio. En general son porcentajes muy bajos de nulos, y podríamos eliminar las filas afectadas con dropna, pero vamos a optar por diferentes alternativas

• Reemplazaremos los valores nulos de la edad (columna numérica) por la media de la columna
• Reemplazaremos los valores nulos del género (columna no numérica) por la moda de la columna
• Eliminaremos las filas que tengan el campo cardio nulo

# Reemplazo de edades nulas por la media
datos['age'].fillna(datos['age'].mean(), inplace=True)
# Reemplazo de géneros nulos por la moda
datos['gender'].fillna(datos['gender'].mode()[0], inplace=True)
# Eliminación de cardios nulos
datos.dropna(subset=['cardio'], inplace=True)

2.2. Tipos de datos de las columnas

Vamos a analizar ahora el tipo de datos de cada columna para ver si es el adecuado. Esto se puede ver fácilmente con la propiedad dtypes del dataset:

datos.dtypes

En nuestro ejemplo podemos ver que las columnas numéricas tienen un tamaño de 64 bits, cuando en realidad podrían ser de 32. También vemos que la columna ap_lo (presión sanguínea baja o diastólica) está marcada como tipo object, no numérica, lo que dificultará su uso en algunas operaciones. Cambiaremos su tipo también a int32:

datos = datos.astype({'age': 'int32', 'height': 'float32', 
  'weight': 'float32', 'ap_hi': 'int32', 'ap_lo': 'int32'})

Nota

En el caso de que una columna tenga valores NA o inf es posible que no admita la conversión a tipo numérico. Habría que convertir o eliminar primero esos valores, para luego tratar el tipo de dato.

2.3. Gestión de anomalías (outliers)

Podemos definir una anomalía como la observación de algún dato que difiere significativamente del resto. Lo que se conoce en términos técnicos como un outlier. Por ejemplo, la siguiente lista contiene medidas de la altura de una puerta realizadas por diferentes personas:

2.1m, 2.3m, 4.5m, 2.2m, 2.4m

Claramente podemos detectar una anomalía en el tercer valor (4.5m) que difiere significativamente del resto. Los datos que extraemos del mundo real a menudo contienen este tipo de anomalías, y es importante detectarlas y gestionarlas aplicando alguna técnica conocida.

2.3.1. Detección gráfica de anomalías

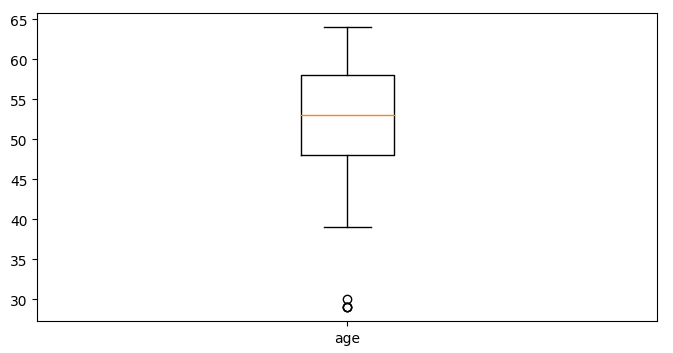
Una primera aproximación a la detección de anomalías (en columnas numéricas) puede ser un gráfico de cajas (box plot), que represente la distribución de los valores de esa columna. Los puntos que queden más allá de los bigotes de las cajas serán las anomalías destacadas de ese campo.

Aplicado a nuestro ejemplo, podemos sacar el diagrama de cajas de las columnas age, height, weight, ap_hi y ap_lo:

# En este caso conviene sacar gráficos separados porque las magnitudes de los datos son diferentes
categorias = ['age', 'height', 'weight', 'ap_hi', 'ap_lo']
for var in categorias:
  fig, ax = plt.subplots(figsize=(8, 4))
  ax.boxplot(labels=[var], x=datos[var])

Se puede ver fácilmente qué valores son anómalos en cada categoría. Aquí vemos el caso de la edad:

2.3.2. Detección de anomalías de forma matemática

Ver las anomalías en un gráfico puede ayudar a hacernos una idea de qué valores son los que hay que controlar en una categoría. Sin embargo, para poder detectarlas en el código y poderlas eliminar/modificar es necesario disponer a veces de algún método matemático. En este apartado proponemos varias alternativas.

Una estrategia habitual es la detección de anomalías basada en la mediana, que considera la mediana de un conjunto de valores como punto de referencia. Esta mediana simplemente es el valor del elemento central de un conjunto ordenado de valores. A partir de esta mediana, se define un cierto umbral alrededor, y cualquier valor que exceda ese umbral se considera una anomalía. Por ejemplo, dado un conjunto de valores en la variable valores y un umbral de 0.3, podríamos detectar qué valores son anómalos de este modo:

import numpy as np
import pandas as pd

valores = ... # Suponemos un conjunto de valores
mediana = np.median(valores)
umbral = 0.3
outliers = []
for elemento in valores:
    if abs(mediana - elemento) > umbral:
        outliers.append(elemento)

Otra alternativa es la detección de anomalías basada en la media. Consiste en utilizar la media de valores como punto de referencia, junto con la desviación típica. Esto evita tener que definir umbrales arbitrarios como en el caso anterior. Simplemente descartamos o anotamos como anomalías todos aquellos valores que excedan el rango de la media más/menos la desviación típica. Así quedaría para el ejemplo anterior:

media = np.mean(valores)        
desviacion = np.std(valores) 
outliers = []
for elemento in valores:
    if media - desviacion > elemento or media + desviacion < elemento:
        outliers.append(elemento)

En el caso de que la desviación típica sea un umbral insuficiente, podemos optar por una variante conocida como puntuación Z, que consiste en definir como umbral un múltiplo de la desviación típica (puntuación Z) que indica a cuántas desviaciones típicas está un valor con respecto a la media:

Z = (valor - media) / desviación típica

Si la puntuación Z excede un cierto umbral razonable, consideramos al valor una anomalía. Aquí vemos cómo quedaría el ejemplo anterior usando una puntuación Z de 1.5:

media = np.mean(valores)        
desviacion = np.std(valores)   
outliers = []
for elemento in valores:
    z = abs(elemento - media) / desviacion
    if z > 1.5:
        outliers.append(elemento)

Finalmente, podemos optar por la técnica del rango intercuartil (IQR, InterQuartile Range). Un cuartil es una medida que divide el conjunto de valores en 4 áreas o intervalos. El rango intercuartil (IQR) es la zona que agrupa las dos áreas intermedias (segundo y tercer cuartil).

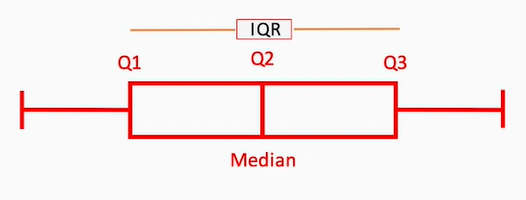
• El primer cuartil (Q1) deja a su izquierda el 25% de los valores
• El segundo cuartil (Q2) es siempre la mediana
• El tercer cuartil (Q3) deja a su izquierda el 75% de los valores

Según esta técnica, todos los valores que queden fuera de este rango IQR se consideran anomalías y deben descartarse. Podemos aplicar algún tipo de umbral para corregir esto e incluir valores que no se diferencien demasiado.

En Python, la función percentile de NumPy automáticamente ordena el vector de valores y calcula los cuartiles o percentiles que le digamos (es decir, los valores que suponen un X% del total de valores). Así quedaría el código en el ejemplo anterior:

import numpy as np
import pandas as pd

# Nos interesan los cuartiles del 25% y 75%
Q1, Q3 = np.percentile(valores, [25, 75])
IQR = Q3 - Q1
outliers = []
for elemento in valores:
    if elemento < (Q1 - 1.5 * IQR) or elemento > (Q3 + 1.5 * IQR):
        outliers.append(elemento)

En este caso, hemos utilizado como umbral 1.5 veces el valor del IQR, descartando los valores que queden más allá, por arriba o por abajo.

2.3.3. Aplicación al ejemplo

¿Qué hacer con los datos que son outliers? Dependerá del problema en sí. Podemos descartarlos (quitarlos de la secuencia original de datos) o imputarlos (asignarles un valor alternativo, como por ejemplo el límite superior o inferior del umbral, entre otras opciones). En nuestro caso tomaremos las siguientes decisiones, en vista de los gráficos de caja obtenidos:

• Ignoraremos las anomalías de la edad, ya que corresponden a pacientes jóvenes (en torno a 30 años) pero podemos tenerlos en cuenta.
• Eliminaremos los registros de pacientes con altura superior a 230 cm
• Asignaremos un umbral inferior de 25 kg a todos los pacientes que pesen menos de esa cantidad (ignoraremos las anomalías de exceso de peso, porque pueden ser reales)
• Eliminaremos todas las presiones sanguíneas (ap_hi y ap_lo) que sean negativas o superiores a una puntuación Z de 2.

# Eliminar pacientes con altura superior a 230 cm
datos = datos[datos['height'] <= 230]

# Asignar 25 Kg a los pacientes que pesen menos de esa cantidad
datos['weight'] = datos['weight'].apply(
    lambda x: 25 if x < 25 else x
)
# Eliminar presiones sanguíneas negativas
datos = datos[(datos['ap_hi'] >= 0) & (datos['ap_lo'] >= 0)]

# Eliminar presiones sanguíneas superiores a Z = 2
# Paso 1: Obtenemos valores anómalos
media1 = datos['ap_hi'].mean()
media2 = datos['ap_lo'].mean()
desv1 = datos['ap_hi'].std()
desv2 = datos['ap_lo'].std()
outliers1 = []
outliers2 = []
Z = 2
for elemento in datos['ap_hi'].values:
    z = abs(elemento - media1) / desv1
    if z > Z:
        outliers1.append(elemento)
for elemento in datos['ap_lo'].values:
    z = abs(elemento - media2) / desv2
    if z > Z:
        outliers2.append(elemento)
# Paso 2: eliminar filas con outliers
datos = datos[~datos['ap_hi'].isin(outliers1)]
datos = datos[~datos['ap_lo'].isin(outliers2)]

Si consultamos la propiedad shape del dataset tras estos pasos de limpieza podremos ver que se han eliminado poco más de 1.000 registros de los 70.000 que teníamos inicialmente, lo que es una cantidad aceptable.

3. Ingeniería de características (feature engineering)

Ahora que ya hemos hecho una limpieza inicial de los datos de entrada, vamos a pasar al proceso de feature engineering. Entre otras cosas, este proceso consiste en:

• Codificar las variables categóricas (textuales) para darles un valor numérico, que es más apropiado para hacer operaciones matemáticas con estos valores de cara a obtener una predicción o resultado final
• Elegir qué características del conjunto de datos son más relevantes para el cálculo que queremos realizar. Es lo que se conoce como feature selection.
• Escalar los valores numéricos en un rango homogéneo, para que no haya valores con una magnitud superior a la de otros.

3.1. Codificación de variables categóricas

En muchas colecciones de datos habrá datos alfanuméricos, también llamados categorizados. Por ejemplo, nombres de ciudades, o calificaciones alfabéticas ("buena", "muy buena"...). Estos datos categorizados no suelen formar parte de algunos análisis por la imposibilidad de hacer operaciones con ellos: no podemos sacar la media de unas ciudades, por ejemplo, o multiplicar una valoración "buena" por un coeficiente numérico.

Para evitar esto y hacer que esos datos también formen parte del problema a resolver, lo que se suele hacer es codificarlos en datos numéricos. Existen para ello distintas estrategias; comentaremos aquí un par de ellas:

• Codificación de etiquetas (label encoding)
• Codificación one hot

3.1.1. Codificación de etiquetas (label encoding)

El etiquetado de datos categóricos consiste en asignar un valor numérico a cada posible valor categórico de una serie de datos. Por ejemplo, imaginemos una tabla como la siguiente, que podría almacenar algunos datos de participantes de un club deportivo:

Nacionalidad	Edad	Peso	Socio
España	34	88.4	Si
Portugal	38	95.6	Si
España	30	90.2	No
Francia	40	96.7	No
Portugal	37	99.3	Si
España	32	82.4	Si

Podemos construir un data frame en Pandas de este modo:

import pandas as pd

datos = { 'Nacionalidad': ['España', 'Portugal', 'España', 
                           'Francia', 'Portugal', 'España'],
          'Edad': [34, 38, 30, 40, 37, 32],
          'Peso': [88.4, 95.6, 90.2, 96.7, 99.3, 82.4],
          'Socio': ['Si', 'Si', 'No', 'No', 'Si', 'Si']
        }

df = pd.DataFrame(datos)

Si quisiéramos establecer una conexión entre los datos de las personas y si son socios o no, no podríamos hacer nada con la nacionalidad, porque es categórica. Tendríamos que asignarle un valor numérico equivalente para poder, por ejemplo, multiplicarla por un coeficiente en una ecuación y establecer así una correlación entre la nacionalidad y la probabilidad de ser socio o no.

Para ello, el primer paso que tendremos que hacer es definir el tipo de dato de la(s) columna(s) afectada(s) como category en lugar del tipo por defecto object que les asigna Pandas:

df['Nacionalidad'] = df['Nacionalidad'].astype('category')

Después, podemos obtener los códigos que automáticamente se han asignado a cada categoría con las propiedades cat.codes, e incluso crear otra columna con ello:

df['Cod_Nacionalidad'] = df['Nacionalidad'].cat.codes

También podemos aplicar este tipo de codificación a la columna Socio, obteniendo los valores alternativos 0 y 1:

df['Socio'] = df['Socio'].astype('category')
df['Cod_Socio'] = df['Socio'].cat.codes

Obtendremos como resultado algo así:

  Nacionalidad  Edad  Peso Socio  Cod_Nacionalidad  Cod_Socio
0       España    34  88.4    Si                 0          1
1     Portugal    38  95.6    Si                 2          1
2       España    30  90.2    No                 0          0
3      Francia    40  96.7    No                 1          0
4     Portugal    37  99.3    Si                 2          1
5       España    32  82.4    Si                 0          1

3.1.2. Codificación one hot

La codificación de etiquetas anterior puede resultar problemática en algunas ocasiones. Al asignar un valor numérico diferente a cada categoría de un conjunto, sin quererlo, se establece un orden. Así, para el ejemplo anterior, si por ejemplo obtenemos que España tiene el valor 0, Portugal el 1 y Francia el 2, si usamos esas codificaciones en un sistema de machine learning se podría llegar a deducir que Francia es mayor o mejor que España porque 2 > 0.

Como ése no suele ser el propósito, una alternativa consiste en utilizar la codificación one hot. Una de las principales características de este tipo de codificación es que no puede haber ninguna relación de orden entre los elementos codificados, porque se codifican en distintas columnas, como veremos a continuación.

Para aplicar codificación one hot con Pandas sobre una columna determinada, podemos emplear el método get_dummies, indicando el data frame con los datos, las columnas que queremos codificar (en el parámetro columns, en forma de lista), y el prefijo que queremos darle a cada nueva columna que se genera. Apliquémoslo a la columna de nacionalidad anterior, de este modo:

df = pd.get_dummies(df, columns=['Nacionalidad'], prefix='Nac')

La función get_dummies devuelve un data frame donde se sustituyen las columnas indicadas por las nuevas. Esto elimina la columna categórica Nacionalidad y la reemplaza por las columnas one hot que se generan. Obtendremos este resultado:

   Edad  Peso Socio  Nac_España  Nac_Francia  Nac_Portugal
0    34  88.4    Si           1            0             0
1    38  95.6    Si           0            0             1
2    30  90.2    No           1            0             0
3    40  96.7    No           0            1             0
4    37  99.3    Si           0            0             1
5    32  82.4    Si           1            0             0

Si no queremos perder la columna categórica por algún motivo, podemos usar la función de este otro modo: lo que hacemos es generar las columnas one hot aparte (sólo pasándole la columna o columnas a codificar, en lugar de todo el data frame), y luego enlazarlas con join al data frame original:

columnas_one_hot = pd.get_dummies(df['Nacionalidad'], 
    columns=['Nacionalidad'], prefix='Nac')
df = df.join(columnas_one_hot)

Obtenemos este otro resultado:

  Nacionalidad  Edad  Peso Socio  Nac_España  Nac_Francia  Nac_Portugal
0       España    34  88.4    Si           1            0             0
1     Portugal    38  95.6    Si           0            0             1
2       España    30  90.2    No           1            0             0
3      Francia    40  96.7    No           0            1             0
4     Portugal    37  99.3    Si           0            0             1
5       España    32  82.4    Si           1            0             0

Como podemos ver, se generan tantas columnas como posibles valores tiene la categoría, y así se pone a 1 la columna a la que pertenece, y a 0 el resto.

3.1.3. Cuándo usar cada tipo de codificación

Existen otros tipos de codificación de datos categóricos que no hemos mencionado aquí, pero el uso de una u otra técnica obedecerá a ciertas premisas en el problema y los datos que estemos manejando.

En general, usaremos codificación one hot cuando no haya ninguna relación de orden entre las categorías, y usaremos label encoding cuando sí pueda haber cierta relación de orden o preferencia entre los valores categóricos. Para la columna Socio del caso anterior podríamos elegir cualquiera de las dos opciones, ya que sólo toma dos valores (0 o 1), e incluso podríamos querer decir que ser socio (1) es "mejor" que no serlo (0), según el problema. También usaremos label encoding para valoraciones, como en el siguiente ejemplo, donde sí interesa establecer un orden o gradación entre las categorías:

Valoración	Codificación
Mala	0
Regular	1
Buena	2
Muy buena	3

Hay que tener en cuenta que, en este caso, los label encoders que hemos utilizado antes no tienen por qué asignar una numeración "correcta" para nuestros intereses, y tendríamos que hacerlo manualmente. Podemos crear una nueva columna paralela a la original Valoracion, llenarla con un valor inicial (cero, por ejemplo), y luego poner el valor a 1 en el caso de valoraciones Regular, 2 para valoraciones Buena, etc.

# Creamos columna Codificacion a partir de la Valoracion
datos['Codificacion'] = datos['Valoracion'].map(
    {'Mala':0, 'Regular':1, 'Buena':2, 'Muy buena':3})

3.1.4. Aplicación al ejemplo

Volvamos a nuestro ejemplo de datos de salud. En el dataset tenemos varias columnas categóricas. Aquí indicaremos lo que vamos a hacer con ellas:

• La columna gender toma los valores M (masculino) o F (femenino). Crearemos una codificación one hot para distinguir con ceros y unos la pertenencia a uno u otro grupo.
• Las columnas cholesterol y gluc pueden tomar los valores Normal, Above Normal y Well Above Normal. En este caso sí nos interesa que haya una gradación o relación de orden, ya que un nivel de colesterol Normal es mejor que uno Above Normal, y éste a su vez es mejor que el Well Above Normal. Para estas columnas usaremos label encoding.
• Las columnas smoke, alco, active y cardio tienen valores Yes/No, que podemos codificar indistintamente como one hot o label encoding, ya que el resultado será el mismo (valores 1/0). Nos aseguraremos, en cualquier caso, que el valor Yes equivalga a 1 y el No a 0.

# Codificación "one hot" de la columna "gender"
datos = pd.get_dummies(datos, columns=['gender'], prefix='Gender')

# Codificaciones "label encoding" de "cholesterol" y "gluc"
datos['cholesterol'] = datos['cholesterol'].map({'Normal':0, 'Above Normal':1, \
    'Well Above Normal':2})
datos['gluc'] = datos['gluc'].map({'Normal':0, 'Above Normal':1, \
    'Well Above Normal':2})

# Codificaciones binarias de columnas SI/NO
datos['smoke'] = datos['smoke'].map({'No':0, 'Yes':1})
datos['alco'] = datos['alco'].map({'No':0, 'Yes':1})
datos['active'] = datos['active'].map({'No':0, 'Yes':1})
datos['cardio'] = datos['cardio'].map({'No':0, 'Yes':1})

# Vemos cómo queda el dataset
print(datos.head())

En algunas ocasiones, la codificación one hot genera información redundante. En nuestro caso, tenemos ahora dos columnas Gender_F y Gender_M que nos indican si un paciente es hombre o mujer. Nos bastaría con una de las dos, ya que si no pertenece a un género automáticamente se le asigna el otro. Así que eliminamos, por ejemplo, la columna Gender_M del estudio.

datos.drop('Gender_M', axis=1, inplace=True)

3.2. Selección de características (feature selection)

Vamos a abordar en este apartado la selección de las características o columnas más relevantes para nuestro estudio. Saber elegir las características correctas o adecuadas para un problema puede repercutir en múltiples ventajas, tales como la reducción del proceso de aprendizaje, el ahorro de memoria de almacenamiento o la simplificación del modelo a considerar. Además, ayuda a evitar la codependencia o colinearidad entre atributos. Es decir, si un atributo depende fuertemente de otro, quizá analizando uno de los dos sea suficiente, y podemos descartar el segundo.

Existen distintas estrategias que nos pueden ayudar a tomar esta decisión. Por ejemplo, podemos entrenar a nuestro sistema con diferentes combinaciones de características, y ver en cuáles se obtienen resultados significativamente diferentes. En nuestro caso vamos a optar por analizar la correlación entre los valores, a través de un mapa de calor de correlación (correlation heatmap) gracias a Pandas y Seaborn. Este mapa nos mostrará de forma gráfica las dependencias entre las diferentes variables involucradas: una correlación alta (cercana a 1) entre dos variables indicará que cuando una aumenta la otra también lo hace, y esto puede significar que una influye mucho en el valor de la otra (y es determinante para calcularlo), o bien que las dos tienen un comportamiento similar (y podemos prescindir de una de ellas). También tenemos que tener en cuenta la correlación inversa (cercana a -1) y ver qué hacer en esos casos.

En definitiva, podemos eliminar características del conjunto por dos motivos:

• Porque sean redundantes (muy correlacionadas con otras que ya vamos a incluir)
• Porque sean irrelevantes (no afecten al resultado que se quiere obtener)

Construimos un mapa de calor de correlación sobre nuestro dataset, de este modo:

plt.figure(figsize=(16, 6))
heatmap = sns.heatmap(datos.corr(), vmin=-1, vmax=1, annot=True)
heatmap.set_title('Correlación datos salud')
plt.show()

Esto generará un gráfico de correlación como este:

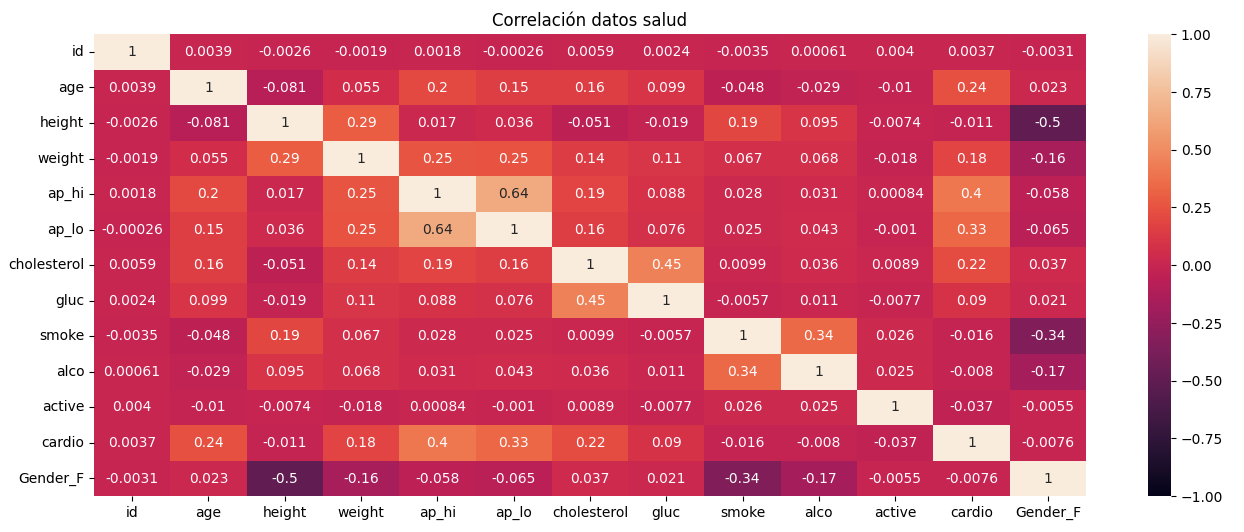
En base a este mapa de correlación, podemos ir a la columna ap_hi, que es la que corresponde a nuestra variable objetivo, y ver qué otras variables son las que más influyen en su valor. Podemos ver que son la presión sanguínea baja (ap_lo), si padece o no problemas cardíacos (columna cardio), el peso (weight), la edad (age) y si tiene o no colesterol. El resto de valores son muy cercanos a 0, es decir, no parecen muy relacionados con la presión sanguínea alta y se pueden eliminar. Además, entre estas variables seleccionadas (ap_lo, cardio, weight, age y cholesterol) no existe una correlación fuerte, lo que nos permitiría eliminar alguna de ellas y quedarnos con un conjunto más reducido.

Vamos entonces a quedarnos únicamente con estas columnas de nuestro dataset:

columnas_relevantes = ['age', 'weight', 'ap_lo', 'cholesterol', 'cardio']
datos = datos[columnas_relevantes + [valor_objetivo]]
datos.head()

3.3. Escalado de características (feature scaling)

El escalado de características o feature scaling es una herramienta muy habitual en el procesamiento de datos. Consiste en dejar un conjunto de valores en un rango común o delimitado. Esto es bastante útil, por ejemplo, en el campo de las redes neuronales. Imaginemos una red que toma imágenes como datos de entrada. Los valores de los colores de esas imágenes pueden estar definidos en distintos rangos, según el formato de la imagen (0 a 255 para imágenes en escala de grises, o valores mayores para algunos modelos de color). En este caso, podría interesar que los valores de los colores de los píxeles estuvieran normalizados en un rango de 0 a 1 para un mejor tratamiento.

Otro ejemplo quizá más ilustrativo. Imaginemos que tenemos datos de clientes de una entidad bancaria. Guardamos su edad, sus ingresos anuales, provincia, etc:

Edad	Ingresos	Provincia
34	28000	Sevilla
40	30000	Toledo
54	32000	Oviedo
43	38000	Badajoz

Si queremos determinar cómo de parecidos o diferentes son dos individuos en base a ciertos datos de entrada (por ejemplo, edad y e ingresos), esto se puede conseguir calculando la "distancia" entre estos dos individuos en base a esos parámetros:

raiz_cuadrada((edad1 - edad2)^2 + (ingresos1 - ingresos2)^2)

El problema aquí lo encontramos en que ingresos y edad se mueven en rangos de valores diferentes, por lo que a la hora de determinar la diferencia entre dos individuos van a ser mucho más determinantes los ingresos, por ser valores mucho más altos. Así, una diferencia de ingresos de apenas 500 euros va a marcar mucho más la diferencia entre individuos que una diferencia de edad de 30 años. Para evitar este problema, podemos escalar los datos a un rango común (por ejemplo, que ambas columnas se muevan en un rango de 0 a 1). Vamos a ver cómo se hace.

3.3.1. Escalado por normalización

Una primera estrategia de escalado es la normalización, también llamada escalado min-max, que deja todos los valores del conjunto en el rango de 0 a 1, aplicando la siguiente fórmula a cada valor:

val_normalizado = (val_actual - val_min) / (val_max - val_min)

Imaginemos un conjunto de datos como este:

import pandas as pd

datosIniciales = {'Nombre': ['Juan', 'Ana', 'Mario', 'Laura'], 
    'Edad': [70, 40, 30, 26], 
    'Sueldo': [2800, 1200, 1750, 1420]}
datos = pd.DataFrame(datosIniciales)

Podemos aplicar el escalado min-max a la colección, aplicándolo a cada columna afectada:

datos['Edad'] = (datos['Edad'] - datos['Edad'].min()) / \
    (datos['Edad'].max() - datos['Edad'].min())

datos['Sueldo'] = (datos['Sueldo'] - datos['Sueldo'].min()) / \
    (datos['Sueldo'].max() - datos['Sueldo'].min())

En el caso de que todas las columnas de la colección sean numéricas y queramos normalizarlas, podemos aplicar una sola fórmula a todo el data frame (no es el caso de este ejemplo):

datos = (datos - datos.min()) / (datos.max() - datos.min())

3.3.2. Escalado por estandarización

Una segunda alternativa consiste en calcular la media y desviación típica del conjunto de datos a tratar. El valor normalizado se calcula entonces como:

val_normalizado = (val_actual - media) / desviación

En este caso, el rango de valores ya no va de 0 a 1, y admite valores negativos, pero al menos está acotado a un rango más controlado. Así quedaría en nuestro ejemplo anterior:

datos['Edad'] = (datos['Edad'] - datos['Edad'].mean()) / \
    datos['Edad'].std()

datos['Sueldo'] = (datos['Sueldo'] - datos['Sueldo'].mean()) / \
    datos['Sueldo'].std()

3.3.3. Aplicación al ejemplo

Vamos a aplicar el escalado a nuestro ejemplo. Las columnas codificadas como one hot no es necesario escalarlas, puesto que ya están acotadas en un rango 0-1. Las columnas codificadas como label encoding podríamos escalarlas si quisiéramos, en el caso de que las etiquetas tuvieran valores más altos. Pero en nuestro caso sólo van del 0 al 2. Así que nos centraremos en la edad, el peso y la presión sanguínea baja. Aplicaremos el escalado por estandarización.

# Escalamos la edad
datos['age'] = (datos['age'] - datos['age'].mean()) / datos['age'].std()
# Escalamos el peso
datos['weight'] = (datos['weight'] - datos['weight'].mean()) / datos['weight'].std()
# Escalamos la presión baja
datos['ap_lo'] = (datos['ap_lo'] - datos['ap_lo'].mean()) / datos['ap_lo'].std()

4. Análisis exploratorio de datos

El análisis exploratorio de datos (EDA) es una etapa que puede darse simultáneamente a las dos anteriores, y nos permite sacar ciertas conclusiones sobre los datos con los que estamos trabajando. De hecho, ya hemos hecho uso de ella cuando hemos mostrado los diagramas de cajas de las columnas numéricas para conocer la distribución de valores y ver posibles anomalías, y también cuando hemos obtenido el mapa de calor de correlación para conocer qué parámetros eran más relevantes para definir el valor objetivo. También cuando hemos empleado el método describe para obtener los datos estadísticos de la columna objetivo ap_hi, y conocer sus valores máximos, mínimos, media, etc.

También podemos obtener otras representaciones numéricas y gráficas, como por ejemplo un histograma con la distribución de valores de la columna objetivo ap_hi, o también gráficos de dispersión (scatter plots) que muestren la dependencia de cada columna relevante con la variable objetivo. Podemos mostrar todo esto en una matriz de 3 filas y 2 columnas, por ejemplo:

fig, ax = plt.subplots(nrows=3, ncols=2, figsize=(12, 10))
for i in range(0, len(columnas_relevantes)):
  fila = i // 2
  columna = i % 2
  ax[fila, columna].scatter(x = datos[columnas_relevantes[i]],
    y = datos[valor_objetivo])
  ax[fila, columna].set_title(columnas_relevantes[i] + " frente a " + valor_objetivo)
ax[2, 1].hist(datos[valor_objetivo], bins=10)
ax[2, 1].set_title("Distribución de valores de " + valor_objetivo)

5. Desarrollo de un modelo simple

Para terminar con este ejemplo vamos a construir un modelo de árbol de decisión que entrene con el conjunto de datos que hemos definido, y mediremos su precisión final (accuracy).

5.1. Definición de la métrica

En primer lugar, vamos a definir la métrica, es decir, una función que determine cómo de bien o mal estamos haciendo nuestra tarea (estimar la presión sistólica). Emplearemos para ello como medida el error absoluto medio (MAE).

def metrica(valores_reales, valores_predichos):
    return mean_absolute_error(valores_reales, valores_predichos)

En este caso el MAE puede resultar adecuado para obtener el error cometido, y nos devolverá cómo nos equivocamos (en promedio) con las estimaciones respecto a los valores reales, calculando la diferencia en valor absoluto entre unas y otras, y obteniendo la media de esos errores.

5.2. Definición de conjuntos de entrenamiento y test

En todo proceso de estimación es necesario disponer de un conjunto de datos con los que "practicar" y entrenar al sistema, y otro conjunto de datos, con resultados conocidos, con los que determinar si el sistema realmente ha aprendido a hacer las cosas adecuadamente o no. Este segundo conjunto se suele denominar datos de validación.

Usaremos la función train_test_split de sklearn para dividir automáticamente nuestro conjunto original de datos en dos partes: una para entrenamiento y otra para validación.

# Indicamos que el 20% de los datos son para test
# El parámetro random_state sirve para que, aleatoriamente, siempre se elijan
# los mismos datos para test.
df_train, df_val = train_test_split(datos, test_size=0.2, random_state=12)

5.3. Definición del modelo

Vamos ahora a definir un árbol de decisión simple para evaluar cómo de bien o mal estima esta presión sistólica con estos datos de entrenamiento y test:

modelo_arbol = DecisionTreeRegressor(random_state=12, max_depth=7,  
    min_samples_split=10)
modelo_arbol.fit(df_train[columnas_relevantes], df_train[valor_objetivo])
predicciones = modelo_arbol.predict(df_val[columnas_relevantes])
error_val = metrica(df_val[valor_objetivo], predicciones)
print(f'Métrica para datos de validación: {error_val}')

Si hemos seguido los pasos de este documento probablemente obtengamos un error promedio en torno a 7.6, es decir, 7 puntos de diferencia entre la presión predicha y la real. Es algo mejorable, pero nos da una idea, en definitiva, de los pasos que se deben seguir para preparar un conjunto de datos de cara a la definición de un modelo.

5.4. Algunas consideraciones finales

Hemos visto durante estos últimos apartados algunas estrategias de escalado y codificación de datos. Nos puede surgir la duda de cuándo aplicar unas u otras, y sobre qué datos de entrada en concreto. Realmente no hay una respuesta universal a esta pregunta, porque va a depender mucho del conjunto de datos de entrada y de lo que queramos hacer con ellos (regresión, clasificación, etc). Pero podemos dar algunas pautas generales a tener en cuenta:

• Normalmente escalaremos columnas que tengan rangos de valores muy dispares entre sí, para aunarlas todas en un rango común (usando normalización o estandarización, como queramos)
• Los valores one hot pueden escalarse o no, hay razones buenas en ambos casos, pero hay que tener en cuenta que, si los escalamos, perderemos esa noción de "pertenencia a una categoría" que nos dan los ceros y unos de cada columna, ya que pasarán a tener otros valores. Es habitual, por tanto, no escalarlos en muchos problemas.
• Los valores a predecir (típicamente conocidos como columna y o variable dependiente) también podemos decidir si escalarlos o no, dependiendo del problema: si estamos en un problema de clasificación, lo normal será no escalarlos, para que se asigne cada registro a una categoría igual a las que teníamos de entrada. Si estamos en un problema de regresión y hemos escalado los parámetros de entrada, es posible que también nos interese escalar el valor de salida (eje vertical).

6. Ejercicios adicionales

A continuación se proponen una serie de ejercicios adicionales para reforzar algunos de los conceptos vistos en este documento, tales como la detección de anomalías, la gestión de valores nulos o la codificación de variables categóricas.

Ejercicio 1

Crea un programa llamado OutliersParquesEolicos.py que utilice este archivo CSV sobre parques eólicos en Castilla y León e identifique los parques que sean outliers en cuanto a potencia total. Aplica la técnica del IQR para identificarlo, tomando como umbral 0.5 veces el IQR

Ejercicio 2

Crea un programa llamado CasasRuralesTelefonos.py que cargue en un data frame los datos de este archivo CSV de casas rurales de la provincia de Castellón. Queremos quedarnos con el id, localidad, nombre y telefono de las casas rurales que tengan un teléfono definido, descartando el resto. El programa debe mostrar por pantalla el listado final procesado, y cuántas casas rurales se han descartado por tener datos nulos. Convierte también la columna telefono a entero de 32 bits, para que no se muestre con decimales.

Ejercicio 3

Crea un programa llamado ParquesEolicosProvinciaGrafico.py que utilice este archivo CSV sobre parques eólicos de la comunidad de Castilla y León. Nos interesa saber la potencia total media de los parques eólicos por provincia, pero algunas potencias totales no están disponibles. Deberás asignarles como valor la moda, y luego mostrar un gráfico de barras como este con los datos finales:

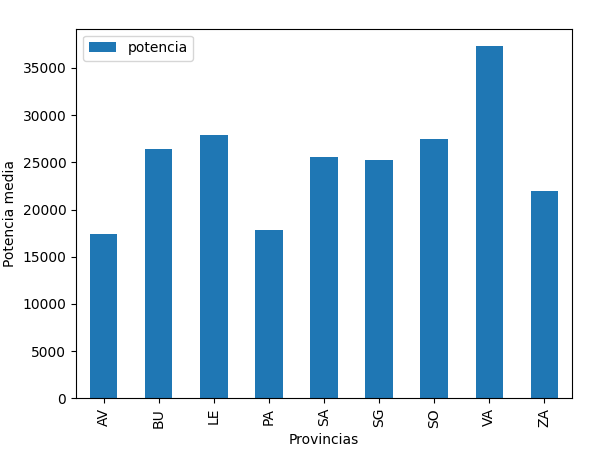
Después, prueba a reemplazar los valores perdidos por la media (en lugar de la moda) y genera de nuevo el gráfico resultante.

Ejercicio 4

Crea un programa llamado DatosParquesEolicos.py que utilice este archivo CSV sobre parques eólicos en Castilla y León y haga lo siguiente:

• Crea una nueva columna llamada potencia_unitaria_norm que normalice los valores de la columna potencia_unitaria entre 0 y 1
• Codifica los valores de la columna provincia usando one hot encoding