Conceptos matemáticos relevantes¶
Para poder trabajar adecuadamente en el mundo del análisis y la ciencia de datos es recomendable conocer y entender ciertos conceptos matemáticos, especialmente algunos relacionados con la estadística y la probabilidad. En este documento vamos a recopilar aquellos más relevantes.
1. Tipos de datos¶
Los datos que podemos manejar para resolver un problema computacional pueden ser de distintos tipos, y tener distintas características.
1.1. Nivel de estructuración¶
Para empezar, podemos catalogar los datos en tres categorías principales:
- Estructurados: son datos organizados en cierto modo, típicamente usando una tabla. En estas tablas, cada observación independiente se refleja en una fila, y cada característica relevante que hemos extraído de ella es una columna de esa fila.
- No estructurados: datos que existen sin una organización o jerarquía determinada, como por ejemplo una imagen, o una opinión en una web.
- Semi-estructurados: no siguen una estructuración rígida en forma de tabla, como los datos estructurados, pero sí se agrupan formando un patrón determinado. Hablaríamos, por ejemplo, de información almacenada en formato XML o JSON.
Evidentemente, a la hora de abordar un problema de IA o de análisis de datos es mucho mejor disponer de datos estructurados o, al menos, semi-estructurados. Pero la inmensa mayoría de información que podemos encontrar en Internet aparece sin estructurar: noticias, vídeos, comentarios, etc. El analista de datos debe ser capaz de acceder a esa información de algún modo, extraer lo que le sea relevante y convertirlo en información estructurada. Es lo que se conoce como pre-procesamiento de los datos.
1.2. Datos cuantitativos y cualitativos¶
Además de lo estructurada que tengamos la información, también podemos hablar de datos cuantitativos o cualitativos. Los datos cuantitativos aportan información numérica, sobre la que se pueden hacer operaciones matemáticas (sumas, medias, etc). Los datos cualitativos aportan información textual o categórica, sobre la que no se pueden aplicar cálculos matemáticos.
Para un programa informático normalmente los datos cualitativos son poco valiosos y, en especial, para modelos de IA no suelen resultar útiles, ya que, a la hora de predecir o inferir un resultado en base a ciertos datos de entrada, lo habitual será hacer algún tipo de cálculo o combinación matemática de esos datos, y esto resultará imposible si los valores no son numéricos. Así que otro proceso importante en el campo del análisis de datos es la cuantificación de los valores cualitativos.
Por su parte, los datos cuantitativos pueden clasificarse a su vez en datos discretos (sólo pueden tomar ciertos valores determinados, como por ejemplo valores enteros sin decimales) y continuos (pueden tomar cualquier valor dentro de un rango numérico determinado).
1.3. Los niveles de datos¶
Cada dato que recopilemos para nuestro análisis puede pertenecer a uno de estos cuatro niveles:
- El nivel nominal se aplica a datos que se describen según un nombre o categoría. Por ejemplo, la nacionalidad de una persona. Es un nivel poco flexible, ya que no permite hacer ninguna operación con esos datos.
- El nivel ordinal proporciona una ordenación de los valores para ese dato. Esto permite ver cuál es mejor o peor, pero no permite otras operaciones como la suma de valores. Por ejemplo, el estado en que se encuentra un vehículo podría catalogarse como Malo - Regular - Bueno, incluso codificarse numéricamente como 0 - 1 - 2. Esto da una idea de cómo de bien o mal está un vehículo, incluso compararlo con el estado de otros.
- El nivel de intervalo se aplica a datos que pueden tomar un valor numérico comprendido en un rango determinado. Por ejemplo la temperatura en una ciudad a lo largo del año se mueve entre ciertos límites determinados. Esto permite hacer operaciones de comparación, ordenación, y también aritméticas, como calcular la media de temperaturas anual.
- El nivel de ratio se aplica a datos numéricos que no tienen un rango específico de valores. Por ejemplo, el saldo en una cuenta bancaria. Podemos aplicar todas las operaciones que se aplicarían con datos de intervalo, pero sin esa limitación de rango.
2. Algunos conceptos básicos¶
Antes de entrar en más materia, vamos a repasar brevemente algunos conceptos matemáticos básicos que usaremos a continuación, para entender mejor a qué nos vamos a referir.
2.1. Vectores, series y matrices¶
Normalmente los datos con que trabajamos en un problema los querremos tener estructurados, como hemos dicho antes. Esto implica disponer las observaciones fila a fila en una tabla, donde cada atributo concreto se ubica en una columna de la tabla.
Entendemos por vector o serie a una secuencia lineal o unidimensional de datos. Por ejemplo, si tenemos una tabla con datos de los socios de un gimnasio, la información completa de uno de esos socios (nombre, dirección, teléfono, etc) sería un vector o serie con los datos de ese socio. Asimismo, la recopilación de todos los nombres de los socios sería un vector (columna) con esa información.
A la tabla completa que recopila toda la información de los socios se le suele llamar también matriz (en este caso, una matriz bidimensional de información, aunque en algunos casos se pueden tener más dimensiones).
2.2. Teoría de conjuntos¶
En algunas ocasiones trabajaremos con datos que forman conjuntos de información. Por ejemplo, el conjunto de socios de un gimnasio. Un conjunto es básicamente una colección de elementos que son distintos entre sí (es decir, no puede haber un mismo elemento repetido).
Un conjunto tiene una magnitud (el número de elementos que forman parte de él), y se pueden aplicar ciertas operaciones elementales sobre dicho conjunto:
- Obtener un subconjunto (elementos del conjunto que cumplan con un cierto criterio, como por ejemplo socios del gimnasio mayores de 60 años)
- Pertenecer a un superconjunto (por ejemplo, el conjunto de los números impares pertenece al superconjunto de los números enteros)
- Obtener elementos comunes entre dos o más conjuntos, operación llamada intersección. Por ejemplo, socios del gimnasio que también estudian inglés en la escuela de idiomas.
- Juntar los elementos de varios conjuntos, operación llamada unión (donde también se eliminarían los elementos duplicados que formaran parte de ambos conjuntos). Por ejemplo, socios del gimnasio junto con los del club de tenis.
- Obtener los elementos de un conjunto que no forman parte de otro (operación conocida como diferencia). Por ejemplo, socios del gimnasio que no son alumnos de la universidad.
3. Estadística¶
La estadística es una rama de las matemáticas que se ocupa de la recolección, organización, análisis, interpretación y presentación de datos. Su objetivo principal es describir y comprender fenómenos a través del uso de datos, permitiendo hacer inferencias o deducciones sobre un conjunto de datos a partir de una muestra representativa de los mismos. Esto se logra mediante la aplicación de diversos métodos y herramientas que ayudan a interpretar la variabilidad de los datos y a tomar decisiones informadas.
Existen dos ramas dentro de la estadística: por un lado está la estadística descriptiva, que se centra en describir los datos objeto de estudio, calculando ciertos parámetros o medidas representativas como la media, desviación típica, etc, para tener una visión clara y completa de lo que suponen. Por otro lado está la estadística inferencial, que busca hacer predicciones o inferencias de nuevos datos en base a los datos de que se dispone.
A continuación explicaremos algunos de los elementos y valores clave que utiliza la estadística descriptiva, qué significan y cómo se calculan, ya que la ciencia de datos hace un uso bastante frecuente de estos valores.
3.1. Muestras y poblaciones¶
En estadística es muy importante distinguir los conceptos de muestra y población. Entendemos por población al conjunto completo de elementos o individuos que nos interesa estudiar. Este conjunto puede llegar a ser muy extenso y, por este motivo, lo que se suele hacer es seleccionar un subconjunto de elementos para hacer el estudio, que es lo que se denomina muestra.
Ejemplo
Por ejemplo, imaginemos que queremos realizar un estudio estadístico sobre las edades de los miembros de un club. El club puede tener miles de socios así que vamos a tomar una muestra de unos pocos. Supongamos (aunque es una reducción demasiado extrema) que elegimos a cinco socios del club, con edades de 20, 22, 28, 58 y 22 años. Utilizaremos este ejemplo en los siguiente subapartados para calcular ciertas variables estadísticas relevantes.
3.1.1. Distribuciones¶
La distribución de un conjunto de valores nos dan una medida de cuántas veces ocurre cada valor en el conjunto, y entre qué rango de valores se mueve dicho conjunto. Esto se suele representar por un tipo de gráfico llamado histograma que representa, para cada posible valor del conjunto (eje horizontal X) cuántas veces se repite en dicho conjunto (frecuencia o densidad, en el eje vertical Y). Por ejemplo, así podría representarse el conjunto de edades de una muestra de individuos:
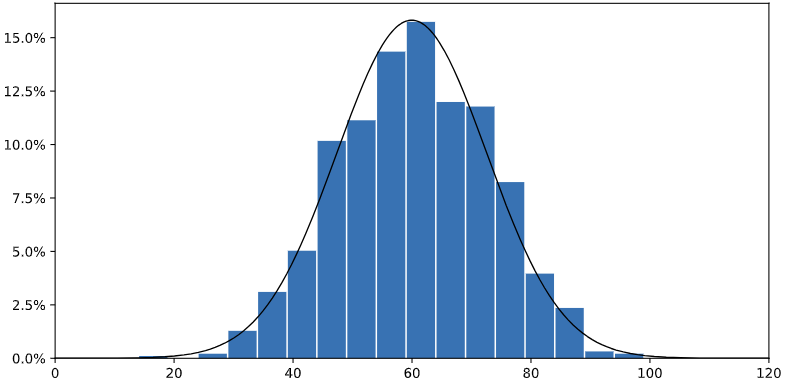
En este caso, podemos observar que el grupo de edad más representado está en torno a los 60 años. Además, la forma que toma la distribución es más o menos simétrica, es decir, la curva de las densidades o frecuencias es más o menos la misma a izquierda y derecha de ese valor máximo central. Es lo que se denomina una distribución normal o gaussiana, ya que la curva de densidad tiene una forma de campana, calculada y definida por el matemático Gauss.
En otros casos las distribuciones son asimétricas, como por ejemplo esta que muestra la distribución de salarios en España en el año 2017 (fuente: El País):
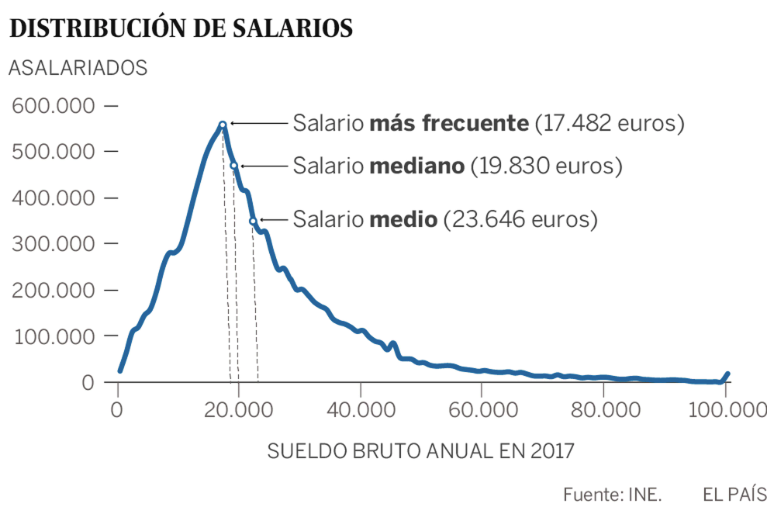
3.1.2. Tipos de muestreo¶
Existen diversas formas en las que elegir la muestra de una población. Comentaremos aquí algunas de las más habituales.
En primer lugar está el muestreo aleatorio, que es el más habitual. Dada una población de individuos, se selecciona un subconjunto de ellos eligiendo cada uno directamente al azar. Todos los individuos de la población tienen la misma probabilidad de ser seleccionados. Como inconveniente podemos destacar que, si la población cuenta con un grupo muy reducido de personas de un determinado colectivo, es posible que dicho colectivo no salga representado en la muestra.
Otro tipo de muestreo es el muestreo estratificado, donde nos aseguramos de que cada subcategoría representada en la población respecto a un campo objeto de estudio salga también en la muestra. Por ejemplo, si tenemos una colección de inmuebles en venta de distintas provincias y queremos hacer estudios estadísticos con ellos, puede resultar interesante que todas las provincias estén representadas en la muestra.
Finalmente, comentaremos el muestreo por cuotas, que consiste en asegurar que un determinado porcentaje de cada categoría va a estar presente en la muestra. Por ejemplo, en un estudio sobre hobbies de empleados de una empresa, puede resultar interesante mantener la misma proporción de hombres y mujeres que los que tenga la empresa en realidad, o incluso alterarlo y hacerlo equitativo (mitad de hombres y mujeres en el estudio).
3.2. Medidas de tendencia central: media, mediana y moda¶
Dado un conjunto de valores (por ejemplo, las edades de las personas de un club), existen ciertos parámetros estadísticos que nos ayudan a determinar en torno a qué valor central giran los datos. Estos parámetros son la media, la mediana y la moda.
- La media es el valor promedio de los datos del conjunto. Se obtiene sumando los valores numéricos de dichos datos y dividiendo el total entre el número de elementos del conjunto. Por ejemplo, para la muestra elegida de personas con edades de 20, 22, 28, 58 y 22 años la media la calcularíamos como
- La mediana es el elemento central de la serie, ordenando los datos de menor a mayor. En el caso de las edades anteriores, si las ordenamos de menor a mayor quedarían 20, 22, 22, 28, 58, y la mediana correspondería al valor 22. En el caso de que el número de valores sea par, se toman los dos valores centrales y se calcula su media.
- La moda es el valor que más se repite en el conjunto de valores dado. En el ejemplo anterior la moda serían 22 años, que se repite 2 veces.
3.2.1. ¿Cuándo utilizar cada valor?¶
Notar que parámetros como la media o la mediana sólo pueden aplicarse sobre valores cuantitativos, ya que no se pueden sumar ni ordenar valores cualitativos. En cambio, la moda es más habitual aplicarla sobre valores cualitativos, viendo cuál es el más frecuente.
En cuanto a la elección entre media y mediana, ¿cuál es el más apropiado? Todo dependerá de la simetría de los datos. Si la distribución de datos que tenemos es asimétrica, la media no va a ser muy representativa. Una distribución de datos es asimétrica si hay más valores a un lado de la media que a otro. Si quedan más valores por debajo de la media, se tiene una asimetría o sesgo positivo, y si hay más valores por encima de la media se tiene una asimetría o sesgo negativo.
Por ejemplo, en el caso anterior la media de 30 años es superior a todas las edades de la muestra, menos la de 58 años. Esto indica que hay una asimetría (positiva) en los valores recogidos, y sería más apropiado usar la mediana (22 años) como valor central.
3.3. Medidas de dispersión: varianza y desviación típica¶
Además de en torno a qué valor giran unos datos, también nos puede interesar conocer cómo de distintos son entre sí. Para ello se utilizan otros dos parámetros estadísticos bastante frecuentes.
- La varianza (representada también como σ2) es la media de los cuadrados de las diferencias entre cada valor y la media del conjunto de datos. En nuestro ejemplo anterior con edades de 20, 22, 28, 58 y 22 años, siendo la media 30 años como hemos calculado previamente, calcularíamos la varianza como:
- La desviación típica (representada también como σ) es la raíz cuadrada de la varianza, lo que la convierte en una medida de dispersión de la misma magnitud que los datos originales (ya que no está elevada al cuadrado). La desviación típica del ejemplo anterior sería de 14.25, lo que significa que los datos se alejan en promedio 14.25 años de la media de 30 años.
3.3.1. Cálculo de la asimetría¶
Utilizando estos nuevos parámetros también podemos calcular de forma numérica la asimetría que comentábamos antes (representada también como γ):
Es decir, calculamos el cubo de la diferencia de cada valor con respecto a la media, y luego obtenemos la media de esos cubos. El resultado lo dividimos entre el cubo de la desviación típica, y tendremos tres opciones:
- Valor de asimetría positivo > 0: existe una asimetría positiva (es decir, la media es mayor que la mayoría de valores de la distribución o, dicho de otro modo, existen valores atípicos hacia la derecha)
- Valor de asimetría negativo < 0: existe una asimetría negativa (es decir, la media es menor que la mayoría de valores de la distribución o, dicho de otro modo, existen valores atípicos hacia la izquierda)
- Valor 0 o cercano: la distribución es más o menos simétrica, es decir, estaríamos ante una distribución normal.
Aplicando esta fórmula al ejemplo anterior de las edades (20, 22, 28, 58 y 22 años, siendo la media 30 años), obtenemos una asimetría de 1.37 (positiva).
3.3.2. Las puntuaciones Z (Z scores)¶
Una vez se conoce el concepto de desviación típica y lo que significa, podemos tomar esa medida como referencia, y calcular cuántas desviaciones típicas se aleja cada dato X de la media. Esto se calcula con la siguiente fórmula:
Un valor cercano a 0 indicará que ese dato está cercano a la media. Un valor cercano a 1 o -1 indica que está alejado exactamente lo que indica la desviación típica (es decir, lo habitual en esa distribución). Un valor mucho mayor que 1 (o mucho menor que -1) indicará que se aleja mucho más que la desviación típica.
Adicionalmente, podemos tomar medidas que sean múltiplos de Z. Así, podemos ver qué valores están más allá de 2 veces la desviación típica, y considerar, por ejemplo, que esos valores están demasiado alejados y son anómalos.
3.3.3. Rangos, percentiles y cuartiles¶
El rango de un conjunto de valores abarca desde su valor mínimo hasta su valor máximo, podemos calcularlo como la diferencia entre ambos valores. Un percentil por su parte, es un valor que deja tras de sí el X% de valores de la muestra. Por ejemplo, el percentil 54 es el valor que deja tras de sí al 54% de valores de la muestra.
Para calcular en qué posición se encuentra el percentil k se aplica esta fórmula:
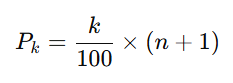
Por ejemplo, dada la secuencia de edades del ejemplo anterior:
20 -22 - 22 - 28 - 58
Si queremos calcular el percentil 40 (es decir, en qué posición dejamos atrás el 40% de los datos), aplicamos la fórmula anterior:
Lo que quiere decir que el percentil 40 se encuentra entre la segunda y tercera posición de la muestra.
Asociado al concepto de percentil está el concepto de cuartil, que permite dividir el rango de valores en cuartos:
- Así, el primer cuartil (Q1) es el valor del conjunto que deja por debajo el 25% de los valores de la muestra.
- El segundo cuartil (Q2) es el valor que deja por debajo el 50% de los valores de la muestra. Es decir, este valor coincide con la mediana del conjunto de valores
- El tercer cuartil (Q3) deja por debajo el 75% de los valores de la muestra.
Una medida estadística relevante es el rango intercuartil (IQR, Inter Quartile Range), que es la diferencia entre el tercer y primer cuartil (es decir, el 50% de valores más centrado de la distribución), y determina cómo de separados están los valores centrales de la distribución.
Gráficamente, el rango intercuartil se representa con una caja desde el valor de Q1 al valor de Q2, seguida de otra caja contigua del valor de Q2 hasta el de Q3. A ambos lados de las cajas se extienden unas líneas llamadas bigotes, que representan valores que, aunque estén fuera de ese rango, están aceptablemente cercanos (normalmente los bigotes miden 1.5 veces el IQR). Más allá de los bigotes, los valores que se hallen se consideran normalmente anomalías.
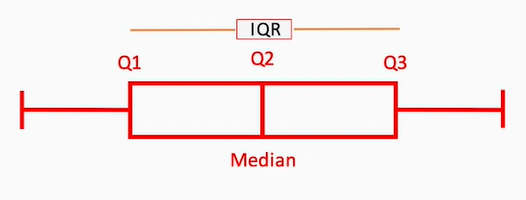
La medida de cada región da también una idea de la simetría de los datos de la distribución. Si las cajas y los bigotes son cortos, significa que los valores están más agrupados; y, si son largos, están más dispersos.
3.4. Intervalos de confianza¶
A la hora de elegir una muestra de una población, nos puede interesar asegurarnos de que la medida que tomamos en la población recoge con cierta fidelidad un parámetro poblacional conocido. En estadística, un intervalo de confianza es un rango de valores que se utiliza para estimar un parámetro poblacional desconocido (como la media o la proporción) con un cierto nivel de confianza. Este intervalo proporciona una estimación de dicho parámetro a partir de los datos de una muestra y refleja la precisión y la fiabilidad de esta estimación.
Por ejemplo, imaginemos que estamos recabando información sobre las horas de sueño diarias que dedican los estudiantes de una universidad, y queremos averiguar con qué precisión se aproxima la media de la muestra seleccionada a la media real de toda la población universitaria. Tenemos que tener en cuenta aquí varios factores:
-
Para realizar el proceso es preciso comenzar por definir el estimador puntual, la estimación del parámetro poblacional que queremos calcular. Por ejemplo, si queremos estimar la media de una población, el estimador puntual sería la media de la muestra.
-
Se debe determinar también el nivel de confianza deseado, es decir, la probabilidad de que el valor real de toda la población esté contenido en lo que calculamos en la muestra. Los niveles de confianza comunes son valores del 90% o más. Por ejemplo, un nivel de confianza del 95% indicaría que, si se repitiera el proceso 100 veces, en 95 de esas veces el intervalo construido contendría el valor verdadero del parámetro. Cuanto mayor nivel de confianza queramos alcanzar, mayor será el rango alrededor del valor obtenido en la muestra.
-
Con estos datos definidos se calcula el intervalo de confianza, es decir, el rango alrededor de la media calculada necesario para garantizar que la población real tiene su valor comprendido en ese intervalo (por ejemplo, 7 horas de sueño \(\pm\) 0.5 horas)
3.4.1. Cálculo de los intervalos de confianza¶
Veámoslo con un ejemplo concreto basado en el caso anterior: supongamos que tomamos una muestra de 6 estudiantes de la universidad. Esos estudiantes han dormido en promedio cada uno 6.6, 6.8, 7.0, 7.1, 7.2 y 7.3 horas diarias. Queremos obtener el intervalo de confianza para un nivel de confianza del 95%.
La fórmula general para calcular el intervalo de confianza es:
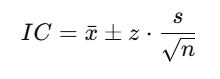
donde:
- x es la media de la muestra (7, en este caso)
- s es la desviación típica de la muestra (0.26)
- n es el tamaño de la muestra (6 estudiantes)
- El valor z es el valor crítico de la distribución, y depende del nivel de confianza que queramos dar y del tamaño de la muestra. Lo explicamos a continuación.
Sobre el valor z
El valor Z es un valor que representa qué cantidad de la distribución hay que tomar para asegurarnos de abarcar el X% deseado (por ejemplo, el 95% en nuestro caso). Para muestras pequeñas (menos de 30 individuos, normalmente) se utiliza una distribución llamada t de Student, que tiene una campana muy ancha para valores pequeños, y el valor final de Z depende de cuántos elementos haya en la muestra (lo que se conoce como grado de libertad). Para muestras más grandes se utiliza una distribución normal estándar.
Dependiendo de la distribución usada, hará falta más o menos franja para abarcar el nivel de confianza deseado. Por ejemplo, para un nivel del 95%, el valor de z es de 2.571 en una distribución t de Student para muestras pequeñas de 5 valores, y de 1.96 para una muestra mayor y una distribución normal estándar. En ambos casos, este valor indica cuántas desviaciones estándar necesitamos abarcar desde la media para capturar ese porcentaje de confianza (es decir, para recoger el 95% de los casos necesitamos \(\pm 2.571\sigma\) en nuestro caso).
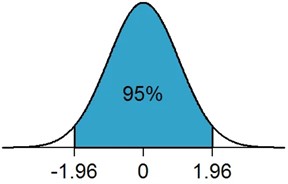
Valor Z para confianza del 95% en distribución normal
Calculando el IC
Resolviendo el cálculo anterior con los valores que hemos dado, calculamos que, para un nivel de confianza del 95%, la media de horas de sueño es de 7 horas diarias \(\pm\) 0.274, lo que significa que con ese nivel de confianza la población total dormirá entre 6.726 y 7.274 horas.
Los intervalos de confianza ayudan a reflejar la precisión de una estimación (cuanto más estrecho sea, más precisa es la estimación) y proporcionan una medida de la incertidumbre en torno al estimador puntual que estamos estudiando.
3.5. Escalados y desplazamientos¶
En algunas ocasiones los datos que hemos recogido en una muestra no tienen un rango de valores adecuado para lo que queremos hacer. Por ejemplo, si tenemos los precios totales de venta de un conjunto de inmuebles, pero queremos ver cuánto supone cada precio con respecto al mayor o al menor, es un dato difícil de calcular. En cambio, si representamos estos precios en un rango de 0 a 1 nos sería más fácil de ver: siendo 1 el valor del inmueble más caro, un inmueble cercano a 0.5 significaría que dicho inmueble es la mitad de caro.
El escalado de un conjunto de datos consiste en multiplicar y/o dividir los valores del conjunto por un factor común, para acotarlos dentro de un rango específico de valores. Por ejemplo, dado el conjunto de precios de inmuebles anterior, si dividimos todos los precios por el precio más alto ya los tendremos todos acotados en un rango de 0 a 1. Es lo que se conoce como normalización, en este caso, aunque hay otros tipos de escalados también habituales, como el escalado por estandarización, que consiste en restarle a cada valor la media y dividir el resultado por la desviación típica. De este modo se calcula cuánto se aleja el valor de la media, tomando como unidad de medida la desviación típica (3 veces la desviación, o -1.2 veces la desviación).
Escalar un conjunto de datos puede tener sus ventajas, porque nos aseguramos de estar trabajando con el mismo rango de valores para todos los datos del estudio, y evitar así que unos sean mucho más grandes que otros.
El desplazamiento (shifting) consiste en sumar/restar un valor a un conjunto de datos, para desplazar sus valores hacia la derecha o hacia la izquierda. Es una operación menos habitual, pero puede resultar útil en algunas ocasiones. Por ejemplo, para transformar todos los valores de un conjunto en positivos, si hay alguno negativo, podríamos sumarle a todos el mismo valor que el valor más negativo que se tenga, quedando éste en 0 y el resto en positivos.
Nota
Observad que si desplazamos un conjunto de valores sumando o restando una cantidad, las medidas de tendencia central (media, mediana y moda) también se verán desplazadas esa misma cantidad. En cambio, las medidas de dispersión (desviación típica, IQR...) no se alterarán. Si optamos por escalar, todas las medidas se verán afectadas en la misma proporción (salvo aquellas que eleven al cuadrado, por ejemplo, como la varianza).
4. Probabilidad¶
La probabilidad es una rama de las matemáticas que estudia el grado de certeza de que un evento ocurra en un experimento aleatorio. Se expresa como un número real entre 0 y 1, siendo 1 una probabilidad total o cierta (100% probable que ocurra el evento) y 0 una probabilidad nula.
4.1. Definición clásica de probabilidad¶
Si un experimento tiene un número N de resultados, y todos son igualmente probables, la probabilidad de que ocurra un evento A se calcula como:
Por ejemplo, si tenemos un dado de 6 caras numeradas, la probabilidad de que salga, por ejemplo, un 3, sería el número de casos en que hay un 3 (una cara) dividido entre el número de resultados posibles (6 posibles caras), es decir:
4.2. Definición frecuentista de probabilidad¶
Si disponemos del gráfico de frecuencias o densidad de los valores de una distribución, podemos calcular gráficamente la probabilidad de un evento. Por ejemplo, dada esta distribución de alturas de individuos:

Si elegimos al azar un individuo del conjunto, la probabilidad de que tenga 60 años sería de algo más del 15% (0.15). La probabilidad de que tenga 60 años o más, teniendo en cuenta que es una distribución normal que deja la mitad de valores a cada lado de la media, sería del 50% aproximadamente (0.5), y la podríamos calcular igualmente sumando las probabilidades (barras) que nos interesan.
La aproximación frecuentista define la probabilidad de este otro modo, en base a los experimentos previos realizados, o los datos previamente recopilados:
Esta metodología frecuentista se apoya en la ley de los grandes números, según la cual, si repetimos un experimento muchas veces, la frecuencia con que ocurre un determinado evento se aproxima a su probabilidad real.
4.3. Algunos conceptos adicionales¶
Antes de ver algunos ejemplos prácticos de la vida real donde podemos aplicar el cálculo de probabilidades, conviene conocer algunos conceptos más asociados a este campo:
Exclusión mutua
Diremos que dos eventos son mutuamente excluyentes si es imposible que sucedan a la vez. Por ejemplo, ser lunes y jueves al mismo tiempo. En este caso, la probabilidad de que se den los dos a la vez \(P(A \cap B)\) es 0.
Eventos complementarios
Dos eventos son complementarios si la no ocurrencia de uno implica la ocurrencia de otro. Por ejemplo, que salga cara (A) o cruz (B) al lanzar una moneda al aire son eventos complementarios. La probabilidad de uno de ellos (B, por ejemplo) se calcula como \(P(B) = 1 - P(A)\)
Probabilidad condicionada
La probabilidad de que suceda un evento A habiendo sucedido antes otro evento B se denota por \(P(A|B)\). Dependiendo de la relación entre estos dos eventos, podemos hablar de independencia o dependencia.
Dos eventos son independientes si el hecho de que se cumpla uno no afecta a la probabilidad del otro. Por ejemplo, sacar un 4 en un dado habiendo sacado antes un 3. En este caso, \(P(A|B) = P(A)\), y también ocurre que \(P(B|A) = P(B)\), y se calcula como hemos visto antes.
Dos eventos son dependientes entre sí si el hecho de que se cumpla uno condiciona la probabilidad del otro. Por ejemplo, si en un mazo de 52 cartas hemos sacado una que es de corazones, ¿qué probabilidad hay de que sea un as?. Si no supiéramos que la carta es de corazones, la probabilidad de que fuera un as sería \(\frac{4}{52}\) pero, sabiendo que es de corazones, la probabilidad sería de \(\frac{1}{13}\) (siendo 13 el total de cartas de corazones que hay). Matemáticamente se expresa de este modo:
Aplicado al ejemplo anterior, \(P(A \cap B)\) es la probabilidad de sacar un as y que sea de corazones, lo que sería $\frac{1}{52}$. Por su parte, \(P(B)\) es la probabilidad de que una carta sea de corazones, que es \(\frac{13}{52}\). Uniendo ambas partes tenemos:
4.3. Algunos ejemplos prácticos¶
Veamos cómo podemos aplicar el cálculo de probabilidades en ejemplos de la vida real. En la siguiente imagen se representan ciertos subconjuntos de pacientes de un hospital:
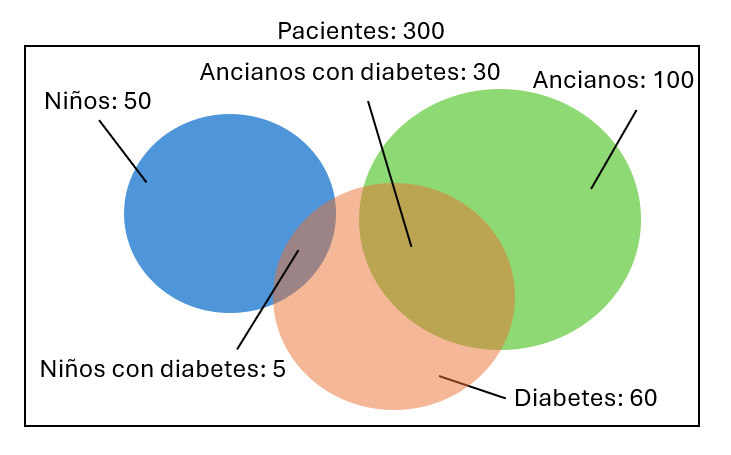
4.3.1. Unión de probabilidades. La regla de la suma¶
Si queremos calcular la probabilidad de que suceda alguno de dos eventos de un conjunto (cualquiera de ellos), esto se calcula sumando las probabilidades de cada evento, en lo que se conoce como regla de la suma. Así, por ejemplo, la probabilidad de que un paciente del hospital sea un niño (A) o un anciano (B) la podremos calcular de este modo:
Sin embargo, si quisiéramos calcular la probabilidad de que un paciente sea niño o tenga diabetes, esta misma fórmula no nos sirve, porque estaríamos sumando dos veces la zona compartida por ambos conjuntos (es decir, estamos sumando dos veces los casos de niños que tienen diabetes). Así, la fórmula general para calcular la probabilidad de que ocurra un suceso u otro es:
En el caso de que los sucesos sean mutuamente excluyentes (como por ejemplo, ser niño y anciano a la vez), \(P(A \cap B)\) es 0, y se tiene simplemente la suma de probabilidades.
4.3.2. Intersección de probabilidades. La regla de la multiplicación¶
Supongamos que queremos calcular la probabilidad de elegir dos pacientes del hospital y que el primero sea un niño y el segundo un anciano.
- La probabilidad de que el primero sea niño la calcularíamos como es habitual, dividiendo el número de casos favorables (50 niños) entre el número de casos posibles (300 pacientes del hospital).
- La probabilidad de que el segundo sea un anciano se calcula dependiendo de cómo elegimos a los pacientes:
- Si después de haber elegido al niño, éste vuelve al conjunto de pacientes, entonces la probabilidad de elegir un anciano sería de 100/300
- Si el niño seleccionado no vuelve al conjunto de pacientes hasta haber seleccionado al segundo, entonces la probabilidad de elegir al anciano sería de 100/299 (ya que hay un paciente menos para elegir)
- La probabilidad conjunta de que pasen ambas cosas se obtiene multiplicando las dos probabilidades. Es lo que se conoce como la regla de la multiplicación
4.3.3. Probabilidad condicionada¶
Supongamos que queremos calcular ahora qué probabilidad hay de que, al elegir un niño, éste tenga diabetes. En este caso estamos hablando de una probabilidad condicionada: vamos a determinar la probabilidad de que un paciente tenga diabetes (suceso A) sabiendo que es un niño (suceso B).
Viendo los datos sobre el gráfico anterior, el número de casos favorables (niños con diabetes) es de 5, y el número de casos posibles (total de niños) es de 50, con lo que la probabilidad sería de 5/50 = 0.1. Si aplicamos la fórmula de la probabilidad condicionada que hemos visto antes obtendremos el mismo resultado:
donde A es el evento "tener diabetes" y B es el evento "ser niño". El evento \(A \cap B\) es ser un niño y tener diabetes, cuya probabilidad es de 5 entre el total de pacientes (300).
4.4. El teorema de Bayes¶
El enfoque bayesiano permite que los datos que vamos acumulando sobre un determinado experimento vayan modificando las percepciones que hacemos de los mismos. En ocasiones partimos de una hipótesis previa de lo que pensamos que puede suceder y, una vez analizamos los datos, éstos nos dan una probabilidad nueva, que configura una nueva hipótesis.
4.4.1. Planteamiento inicial¶
Supongamos que dos trabajadores, Ana y Juan, están moderando contenidos en una red social. Ana elimina contenidos ofensivos el 50% de las veces, y Juan el 30%, y los dos revisan a diario aproximadamente la misma cantidad de contenidos. Sabiendo que un contenido ha sido eliminado, ¿qué probabilidad hay que haya sido Ana?
Para resolver el problema nos planteamos varios elementos:
- Llamaremos H a la hipótesis que queremos averiguar, es decir, si ha sido Ana
- Llamaremos D a los datos que conocemos: un contenido ha sido eliminado
- P(H|D) es la probabilidad de que haya sido Ana quien eliminó el contenido
- P(D|H) es la probabilidad de un contenido haya sido eliminado sabiendo que lo hizo Ana
- P(H) es la probabilidad de que Ana revise un contenido
- P(D) es la probabilidad de que un contenido se elimine
4.4.2. Fórmula del teorema¶
El teorema de Bayes dice que la probabilidad de que ocurra un suceso H habiendo ocurrido uno D es igual a la probabilidad de que pase D habiendo ocurrido H multiplicado por la probabilidad de H y dividido por la probabilidad de D:
Necesitamos conocer los valores de las tres probabilidades de la parte derecha para poder resolver nuestro problema. Veamos si es así:
- P(D|H) es la probabilidad de que un contenido se elimine si fue Ana quien lo revisó. Según el enunciado eso ocurre el 50% de las veces (0.5)
- P(H) es la probabilidad de que Ana haya revisado el contenido. Teniendo en cuenta que los dos revisan la misma cantidad diaria aproximadamente, nuevamente esta probabilidad la podemos asignar a 0.5
- P(D) es la probabilidad de que un contenido haya sido eliminado. Y aquí existen dos opciones:
- Que el contenido lo haya revisado Juan y lo haya eliminado. Combinando ambas probabilidades tendríamos 0.5 de que lo revise Juan y 0.3 de que, siendo Juan, lo haya eliminado, es decir 0.5 · 0.3 = 0.15
- Que el contenido lo haya revisado Ana y lo haya eliminado. Nuevamente combinamos ambas probabilidades: 0.5 de que lo revise Ana y 0.5 de que, siendo Ana, lo haya eliminado, es decir 0.5 · 0.5 = 0.25
- Como queremos calcular la probabilidad de que un contenido se elimine, y no hay más revisores, será la probabilidad de uno o la del otro. Aplicando la regla de la suma tenemos una probabilidad conjunta de 0.15 + 0.25 = 0.4.
Unimos ahora todas las piezas del puzzle para calcular la probabilidad de que, habiéndose eliminado un contenido, haya sido Ana:
Es decir, si un contenido ha sido eliminado, hay un 62.5% de probabilidades de que lo haya hecho Ana.
4.5. Aplicaciones de la probabilidad¶
Veremos a continuación algunos ejemplos prácticos donde se aplica la probabilidad en problemas que tienen que ver con el análisis y la ciencia de datos.
4.5.1. Aplicando el teorema de Bayes¶
¿Qué aplicaciones puede tener el teorema de Bayes en el campo del Data Science? Podemos emplearlo en tareas que tengan que ver con la predicción de resultados o actualización de probabilidades basadas en nuevos datos.
Por ejemplo, imaginemos que tenemos una base de datos de correos, y los tenemos clasificados como "spam" o normales. Ahora queremos saber qué probabilidad hay que de un correo que tiene la palabra "oferta" sea "spam".
- P(spam|oferta) es lo que queremos calcular: la probabilidad de que un correo sea "spam" dado que tiene la palabra "oferta"
- P(oferta|spam) es la probabilidad de que un correo que tenga la palabra "oferta" sea "spam".
- P(oferta) es la probabilidad de que un correo tenga la palabra "oferta"
- P(spam) es la probabilidad de que un correo sea spam
Combinando estas tres últimas probabilidades (podemos sacar las estadísticas pertinentes de nuestra base de datos) podemos calcular la probabilidad que buscamos, aplicando el teorema de Bayes. Además, si añadimos este nuevo veredicto a nuestra base de datos, modificamos la probabilidad de este evento para futuras predicciones.
4.5.2. Clasificadores binarios. Matrices de confusión¶
Imaginemos que se ha desarrollado un modelo para predecir si una persona tiene o no cáncer de piel. Se ha aplicado el modelo a un grupo de personas de todo tipo (con y sin cáncer) y habremos obtenido cuatro tipos distintos de resultados:
- Personas sanas a las que no se les detecta cáncer
- Personas sanas a las que sí se les detecta cáncer
- Personas enfermas a las que no se les detecta cáncer
- Personas enfermas a las que sí se les detecta cáncer
Este modelo es lo que se denomina un clasificador binario, es decir, clasifica los resultados en dos categorías posibles (con o sin cáncer, en este caso). Los resultados de la evaluación del modelo se pueden representar en una matriz de 2x2 casillas, llamada matriz de confusión
| Test negativo | Test positivo | |
|---|---|---|
| Pacientes sanos | 123 | 14 |
| Pacientes enfermos | 8 | 187 |
Los datos 123 y 187 son los correctos, lo que se denominan respectivamente verdaderos negativos y verdaderos positivos. Es decir, personas sanas que han dado negativo en el test y personas enfermas que han dado positivo en el test.
Lo que hace que el modelo falle o no sea del todo correcto son los otros dos datos:
- El dato de 14 son los falsos positivos, también llamados errores de tipo I, es decir, personas sanas que han dado positivo en el test.
- El dato de 8 son los falsos negativos, también llamados errores de tipo II, es decir, personas enfermas que han dado negativo en el test.
Tratar de minimizar estos dos datos es crucial cuando elaboramos un modelo de IA, ya que un sistema que no diagnostique cáncer en una persona que sí lo tenga puede resultar en un error fatal.
En lo que al cálculo de probabilidades se refiere, la probabilidad de que el modelo anterior dé un falso positivo la calcularíamos dividiendo el número de falsos positivos obtenidos (14) entre el total de pacientes sanos procesados (123 + 14 = 137), obteniendo un 10.21% de probabilidad. Haríamos lo mismo con los falsos negativos, usando los datos de la segunda fila en ese caso: 8 / 195 = 4.10%.
4.5.3. Generación de datos aleatorios¶
En algunas ocasiones nos puede interesar generar datos aleatorios para probar el funcionamiento de nuestros programas. Es posible que esos datos tengan una distribución uniforme, es decir, todos tengan la misma probabilidad, como por ejemplo simular el lanzamiento de un dado; en este caso bastaría con generar un número aleatorio entre 1 y 6, utilizando para ello cualquier función disponible en varios lenguajes de programación. Aquí vemos algunos ejemplos:
// Generación de un número entero aleatorio entre 1 y 6 con las mismas
// probabilidades, usando Java
java.util.Random r = new java.util.Random();
int dado = 1 + r.nextInt(6);
# Generación de un número entero aleatorio entre 1 y 6 con las mismas
# probabilidades, usando Python
import random
dado = random.randint(1, 6)
Sin embargo, en otras ocasiones los datos no son equiprobables. En el ejemplo del hospital anterior, la probabilidad de que un paciente sea niño es de 50/300 = 16.67%, mientras que la de ser un anciano es de 100/300 = 33.33%. Supongamos que queremos generar al azar un nuevo paciente ficticio, y queremos que su edad esté acorde a las proporciones existentes, es decir, que sea niño un 16.67% de las veces, anciano un 33.33% de las veces y adulto el resto de veces (50%).
Por concretar aún más, queremos generar la edad del paciente según esta distribución:
- El paciente tendrá entre 0 y 17 años (inclusive) el 16.67% de las veces
- Tendrá entre 65 y 100 años (inclusive) el 33.33% de las veces
- Tendrá entre 18 y 64 años (inclusive) el 50% de las veces
En este caso las instrucciones anteriores no nos sirven, porque si pedimos que genere una edad al azar entre 0 y 100 años, todas las edades tendrán la misma probabilidad. Hace falta utilizar estrategias alternativas. Por ejemplo, la instrucción random.choices de Python permite generar un número aleatorio indicando rangos de probabilidad. Nos podría quedar así:
rangos = [
range(0, 18), # 0 al 17
range(65, 101), # 65 al 100
range(18, 65) # 18 al 64
]
probabilidades = [0.1667, 0.3333, 0.5]
# Seleccionar un rango basado en las probabilidades
rango_seleccionado = random.choices(rangos, probabilidades)[0]
# Generar un número aleatorio dentro del rango seleccionado
edad_aleatoria = random.choice(rango_seleccionado)