Introducción al análisis de datos¶

Los datos que utiliza una aplicación son un componente fundamental de la misma, hasta el punto de que, si los datos no son correctos o apropiados, la aplicación no va a poder desempeñar su tarea correctamente. El data science o ciencia de datos es una disciplina que emplea diferentes métodos para analizar y procesar los datos de un determinado proyecto, con el fin de extraer información significativa.

Dentro de esta ciencia de datos existen diferentes ramas o subprocesos bastante relevantes. En este documento veremos algunos de los más importantes, que son:

El data cleaning (limpieza de datos), es un proceso que se desarrolla antes de que los datos puedan utilizarse para modelado. Es crucial asegurarse de que estén limpios y estructurados correctamente.
El feature engineering (ingeniería de características), es otro proceso que normalmente se inicia después del anterior para, una vez que los datos están limpios y correctamente estructurados, ver si es necesario prescindir de algunos de ellos, o generar o transformar otros.
El EDA (exploratory data analysis, análisis exploratorio de datos) consiste en examinar y visualizar los datos para comprender mejor su naturaleza y patrones. Comprende habitualmente la generación de distintos gráficos y la obtención de ciertas estadísticas descriptivas (medias, desviaciones típicas, modas, etc). No existe un acuerdo general sobre si este paso debe hacerse antes o después de los anteriores. No necesariamente tenemos que limpiar los datos antes de analizarlos, ni al revés. Dependiendo del problema, es posible que primero necesitemos cierto conocimiento de los datos (proporcionado por el EDA) antes de poderlos limpiar o, por el contrario, que necesitemos procesar los datos y completarlos adecuadamente antes de poderlos analizar.

Para ilustrar los pasos que describiremos a continuación partiremos de un conjunto de datos de ejemplo: imaginemos que tenemos una tabla con las características de distintos inmuebles: localidad, inmobiliaria que lo vende, superficie, número de habitaciones, año de construcción, si tiene o no ascensor y piscina, estado y precio:

Localidad	Inmobiliaria	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
Alicante	InmoAlicante	90	3	2002	Si	No	Bueno	180.000
Elche	SuPiso	110	4	2021	No	Si	Nuevo	260.000
Alicante	TeleCasa	-	3	1991	Si	No	Origen	165.000
San Vicente	SuPiso	100	4	1995	No	No	-	170.000
San Vicente	-	80	2	-	Si	No	Bueno	1.500.000
...	...	...	...	...	...	...	...	...

Para contextualizar más aún el ejemplo, supongamos que queremos desarrollar una aplicación que, dados unos parámetros de un inmueble, nos ayude a predecir o estimar un precio de venta al público.

1. Data cleaning¶

Como hemos comentado, la limpieza de datos o data cleaning comprende una serie de tareas que se destinan a limpiar, estructurar y dar formato al conjunto de datos de un problema determinado. En esta etapa debemos responder y resolver preguntas como:

¿Me faltan valores en los datos recopilados?
¿Hay algún valor que no parezca adecuado o desentone con el resto?
¿Los datos tienen un formato válido o adecuado?
...

En concreto, la etapa del data cleaning comprende las siguientes tareas:

Gestión de valores faltantes (missing values): identificaremos casillas que no tengan valor, y decidiremos qué hacer con ellas
Detección de valores atípicos (outliers): identificaremos casillas que tengan valores demasiado alejados del resto de valores de su columna y, nuevamente, decidiremos qué hacer con estos valores, ya que pueden distorsionar el análisis.
Detección de duplicados: detectaremos si existen filas duplicadas en el conjunto, eliminando las que lo sean.
Validación de datos: verificaremos que lo datos introducidos tienen el formato y la precisión adecuada. Por ejemplo, que los valores numéricos reales tengan el correspondiente separador decimal, o que las fechas vengan en un formato adecuado.
Documentación del proceso: mantendremos un registro de los pasos realizados en el proceso de limpieza para futuras referencias y auditorías.

A continuación veremos ejemplos de algunas de estas etapas, aplicadas al ejemplo de los inmuebles.

1.1. Gestión de valores faltantes (missing values)¶

Si echamos un vistazo a la tabla de inmuebles vista inicialmente, vemos que nos faltan algunas casillas por completar:

Superficie del tercer inmueble
Estado del cuarto inmueble
Inmobiliaria y año de construcción del quinto inmueble
...

¿Qué estrategias o decisiones podemos tomar en estos casos? Dependiendo del valor en cuestión podemos optar por:

Eliminar la fila afectada. Esto se puede hacer si disponemos de muchos datos de entrada, y la cantidad de filas que vamos a eliminar no es relevante respecto al total
Sustituir el valor faltante por la media de valores de la columna, en el caso de valores numéricos
Sustituir el valor faltante por la moda de los valores de la columna (es decir, el valor más repetido o habitual). Esto se puede aplicar tanto a valores numéricos (sobre todo valores enteros) como a valores categóricos (textos).

En nuestro caso, podríamos decidir lo siguiente:

Sustituir la superficie del tercer inmueble por la media de superficies que tengamos
Sustituir el estado del cuarto inmueble por la moda de estados (estado más repetido en la columna)
Sustituir la inmobiliaria y el año de construcción del quinto inmueble por la moda de esas columnas. Notar que calcular la media de año de construcción podría dar un valor real (con decimales). En este caso tendríamos que redondearlo al entero más cercano.

Con esto, nuestra tabla de inmuebles podría quedar así:

Localidad	Inmobiliaria	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
Alicante	InmoAlicante	90	3	2002	Si	No	Bueno	180.000
Elche	SuPiso	110	4	2021	No	Si	Nuevo	260.000
Alicante	TeleCasa	95	3	1991	Si	No	Origen	165.000
San Vicente	SuPiso	100	4	1995	No	No	Bueno	170.000
San Vicente	SuPiso	80	2	1995	Si	No	Bueno	1.500.000
...	...	...	...	...	...	...	...	...

El proceso de sustuituir valores faltantes por otros generados normalmente se conoce como imputación de valores en el campo del data science.

1.2. Detección de anomalías (outliers)¶

Una anomalía (outlier en inglés) es un valor que difiere significativamente del resto. Por ejemplo, si estamos analizando datos de clientes, y todos ellos están entre 20 y 40 años, puede ser anómalo encontrar un cliente de 67 años. Quizá a la hora de introducir el dato alguien se equivocó, y el cliente en cuestión tenía 37 años.

En nuestro ejemplo de inmuebles, hay una anomalía clara en la columna Precio, pues el precio del quinto inmueble es de 1.500.000 euros, que no se asemeja a ninguno de los precios introducidos en esa columna. ¿Qué hacer cuando detectamos una anomalía? Básicamente las alternativas que tenemos son las mismas que cuando detectamos un valor faltante: prescindir de la fila afectada o reemplazar la anomalía por un valor más representativo (media, moda, valor más alto o valor más bajo del conjunto, por ejemplo).

Pero... ¿cómo determinamos que un valor es efectivamente una anomalía? Existen diferentes técnicas para ello:

Detección basada en la mediana: una estrategia habitual es considerar la mediana del conjunto de valores. Esta mediana simplemente es el valor del elemento central de un conjunto ordenado de valores. A partir de esta mediana, se define un cierto umbral alrededor, y cualquier valor que exceda ese umbral se considera una anomalía. Por ejemplo, en el caso de los precios, si la mediana es 207.000, por ejemplo, podemos establecer un umbral de 100.000 euros, y todo lo que exceda (por arriba o por abajo) de ese umbral se considerará una anomalía.
Detección basada en la media: similar a la anterior, pero se toma la media como referencia. Como umbral en este caso se suele calcular la desviación típica, que determina de algún modo cuánto se alejan en promedio los valores individuales de un conjunto de datos respecto a su promedio o media. Así, por ejemplo, si la media de precios es de 190.000 y la desviación típica es de 70.000, podemos marcar como anomalía todo lo que esté por debajo de 120.000 o por encima de 260.000.
Detección basada en la puntuación Z: basándonos en el caso anterior, puede que no nos sirva sólo la desviación típica, sino que queremos incluir como válidos también precios que estén 2 o 3 veces más allá de la desviación típica. Así, marcamos un umbral arbitrario (por ejemplo, 2 veces la desviación típica) y lo usamos para marcar como anómalos los valores que excedan (por encima o por debajo) de ese umbral.
Detección basada en rango intercuartil: los valores que conforman una serie de datos se agrupan en cuartiles, de forma que la distribución se agrupa en 4 franjas o intervalos: Q1 (valores inferiores), Q2, Q3 y Q4 (valores superiores). El rango intercuartil (IQR, Inter Quartile Range) es la zona que agrupa los cuartiles intermedios. Todo lo que quede fuera de este rango IQR se puede considerar una anomalía, o bien considerar un umbral u y considerar anomalía todo lo que quede a u unidades de este rango IQR.

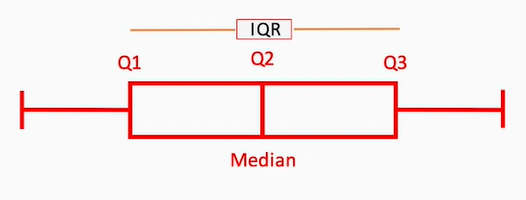
En nuestro ejemplo, una vez hemos detectado las anomalías (el precio de 1.500.000 euros) podemos reemplazarlas, por ejemplo, por el valor medio de la columna. Podría quedar así:

Localidad	Inmobiliaria	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
Alicante	InmoAlicante	90	3	2002	Si	No	Bueno	180.000
Elche	SuPiso	110	4	2021	No	Si	Nuevo	260.000
Alicante	TeleCasa	95	3	1991	Si	No	Origen	165.000
San Vicente	SuPiso	100	4	1995	No	No	Bueno	170.000
San Vicente	SuPiso	80	2	1995	Si	No	Bueno	190.000
...	...	...	...	...	...	...	...	...

2. Feature engineering¶

La ingeniería de características es un proceso posterior a la limpieza de datos. Una vez hemos tratado los valores nulos, las anomalías, y todo lo comentado en el punto anterior, llega el momento de formularnos nuevas preguntas:

¿Me sirven todos los campos (columnas) que tengo?
¿Puedo hacer operaciones con todas las columnas con que me he quedado, o hay alguna(s) que podría codificar de otra forma?
¿Los valores de todas las columnas tienen el mismo peso o relevancia en la operación que voy a realizar?

Más concretamente, la etapa del feature engineering comprende las tareas siguientes:

Selección de características: identificar las características más relevantes y significativas para el problema en cuestión y descartar las que puedan ser redundantes o irrelevantes.
Creación de nuevas características: puede que nos interese obtener alguna información nueva de la que no disponemos. Esto a menudo implica combinar variables que ya tenemos en nuestros datos. Por ejemplo, si tenemos disponible cuántos años ha trabajado un empleado en una empresa y cuántos proyectos ha desarrollado, nos puede interesar calcular cuántos proyectos ha desarrollado por año, haciendo una división entre los dos valores existentes.
Codificación de variables categóricas: convertir variables textuales en representaciones numéricas adecuadas para los modelos, para poder hacer cálculos matemáticos con ellas.
Normalización y escala: ajustar las características para que tengan una escala uniforme, lo que es particularmente importante para algoritmos sensibles a la escala, como las máquinas de soporte vectorial (SVM) y el k-means.
Extracción de características: similar a la anterior, pero se utilizan técnicas más avanzadas, como análisis de componentes principales (PCA) o reducción de dimensionalidad, para extraer características latentes o reducir la complejidad del conjunto de datos.

Veamos a continuación cómo afrontar algunas de estas tareas.

2.1. Selección de características (feature selection)¶

La selección de características es una tarea que consiste en, dado un conjunto de datos, determinar qué columnas son o pueden ser relevantes para la tarea que debemos llevar a cabo, y qué otras columnas son irrelevantes o redundantes. Volviendo a nuestro ejemplo, si queremos calcular el precio de venta final de un inmueble dados unos parámetros de entrada (localidad, inmobiliaria, superficie, etc), es posible que, por ejemplo, el nombre de la inmobiliaria no importe mucho para calcular su precio final, y podamos prescindir de él. En este caso nos quedaríamos con esta tabla.

Localidad	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
Alicante	90	3	2002	Si	No	Bueno	180.000
Elche	110	4	2021	No	Si	Nuevo	260.000
Alicante	95	3	1991	Si	No	Origen	165.000
San Vicente	100	4	1995	No	No	Bueno	170.000
San Vicente	80	2	1995	Si	No	Bueno	190.000
...	...	...	...	...	...	...	...

A la hora de decidir qué columnas son relevantes y cuáles no se pueden utilizar ciertos cálculos, como la correlación de variables. Esta correlación indica cómo de relacionada está cada pareja de variables del estudio. Si existe una correlación alta (cercana a 1) quiere decir que el aumento de una variable influye significativamente en el aumento de otra. Si la correlación es baja (cercana a -1) es una relación inversa: el aumento de una variable influye mucho en el descenso de la otra. Si la correlación es neutra (cercana a cero) no existe una relación importante entre estas variables.

Existen algunas representaciones gráficas que nos ayudan en esta tarea, como los mapas de calor de correlación (correlation heatmaps) que pintan de distintos colores las correlaciones entre las diferentes variables, en una tabla bidimensional. Echemos un vistazo a este mapa:

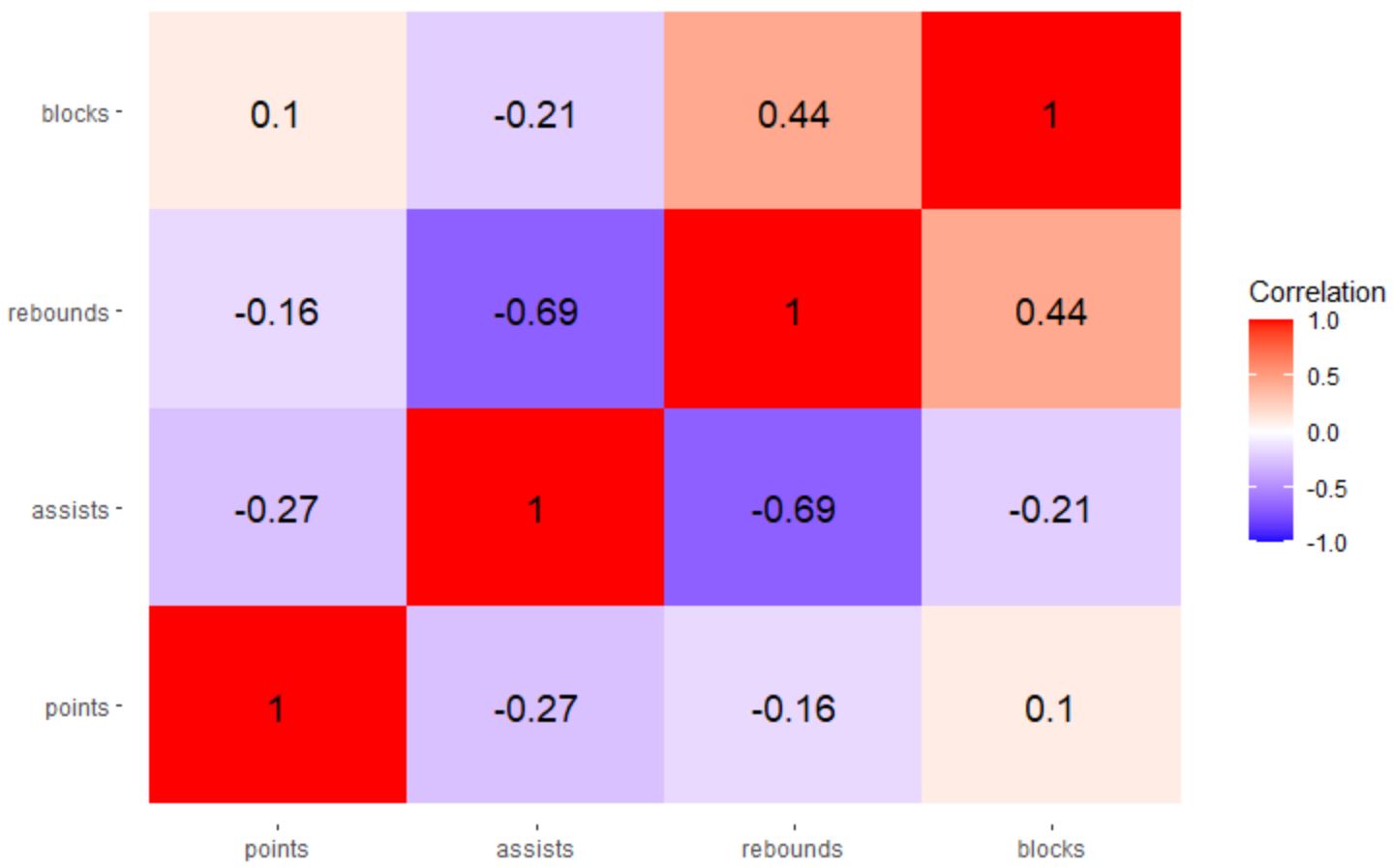
En él se representa la relación entre diferentes estadísticas de jugadores de baloncesto: tapones (blocks), rebotes, asistencias y puntos anotados. Estos campos se ponen tanto en filas como en columnas, de modo que la correlación en la diagonal principal siempre es 1 (un dato influye totalmente sobre sí mismo). Sin embargo, esto nos ayuda a obtener cierta información adicional interesante. Por ejemplo:

Existe cierta correlación entre los rebotes (rebounds) y los tapones (blocks) ya que normalmente la persona que captura rebotes es la misma que hace los tapones (gente alta, los pívots)
Existe una correlación inversa entre las asistencias (assists) y los rebotes, porque normalmente las asistencias las dan los bases, no los pívots, y los bases son quienes menos rebotes capturan

2.2. Codificar variables categóricas¶

Entendemos por variable categórica una variable que toma un número limitado de valores (normalmente no numéricos). En nuestro caso, por ejemplo, la localidad de los inmuebles es una variable categórica, limitada a las localidades que forman parte del estudio. También lo es el estado del inmueble, que podría definirse como una clasificación en tres o cuatro niveles: Para reformar, Origen, Bueno y Nuevo, por ejemplo.

Sin embargo, pensemos un poco. ¿Cómo podríamos hacer para calcular el valor final de un inmueble dadas su localidad, superficie, estado, número de habitaciones...? Un primer supuesto lógico podría ser establecer algún tipo de conexión matemática entre estos datos, como por ejemplo una combinación lineal: multiplicar cada campo por un coeficiente y sumarlos:

Precio = a₁·Localidad + a₂·Superficie + a₃·Habitaciones + ...

Llegados a este punto, ¿cómo podemos multiplicar "Alicante" por un valor numérico? Es imposible. Es necesario codificar este dato de forma numérica para poder hacer operaciones con él. Existen dos formas principales de hacer esta codificación:

Label encoding
Codificación one hot

El label encoding consiste en asignar a cada valor categórico un valor numérico asociado, consecutivamente. Así, podríamos asignarle a Alicante el valor 1, a Elche el valor 2, a San Vicente el valor 3... y así sucesivamente para cada nueva localidad que encontremos en la columna. Y lo mismo podríamos hacer en la columna de Estado: asignar a Para reformar el valor 1, a Origen el valor 2, etc.

Sin embargo, esta codificación presenta un problema: establece una relación de orden que, dependiendo del modelo de aprendizaje que desarrollemos, puede ser perjudicial. Dicho de otro modo, el modelo que programemos podría "aprender" que, dados los valores numéricos, el valor de Alicante (1) es mejor o peor que el de San Vicente (3) sólo porque el número es menor, o mayor, cuando, en realidad, esa columna no tiene ninguna relación de orden entre sus valores (no hay ninguna localidad mejor o peor que otra). Para evitar esta asignación artificial, la codificación one hot lo que hace es codificar de forma binaria cada localidad. Esto se consigue asignando una columna nueva a cada localidad, y marcando como 1 o 0 la localidad a la que pertenece el inmueble (sólo habrá un 1 por fila, en la localidad correspondiente). Así nos quedaría para las localidades de los inmuebles, suponiendo que sólo hay 3 (Alicante, Elche y San Vicente):

Alicante	Elche	San Vicente	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
1	0	0	90	3	2002	Si	No	Bueno	180.000
0	1	0	110	4	2021	No	Si	Nuevo	260.000
1	0	0	95	3	1991	Si	No	Origen	165.000
0	0	1	100	4	1995	No	No	Bueno	170.000
0	0	1	80	2	1995	Si	No	Bueno	190.000
...	...	...	...	...	...	...	...	...	...

¿Qué ocurre con el Estado de los inmuebles? Aquí sí hay una relación de orden, ya que un inmueble Bueno es mejor que un inmueble que esté de Origen. Podemos asignar una codificación consecutiva 1, 2, 3, 4 a los estados Para reformar, Origen, Bueno y Nuevo, respectivamente, quedando así:

Alicante	Elche	San Vicente	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
1	0	0	90	3	2002	Si	No	3	180.000
0	1	0	110	4	2021	No	Si	4	260.000
1	0	0	95	3	1991	Si	No	2	165.000
0	0	1	100	4	1995	No	No	3	170.000
0	0	1	80	2	1995	Si	No	3	190.000
...	...	...	...	...	...	...	...	...	...

Lo mismo ocurre con los valores booleanos Si/No, podemos codificarlos como 1 y 0, respectivamente:

Alicante	Elche	San Vicente	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
1	0	0	90	3	2002	1	0	3	180.000
0	1	0	110	4	2021	0	1	4	260.000
1	0	0	95	3	1991	1	0	2	165.000
0	0	1	100	4	1995	0	0	3	170.000
0	0	1	80	2	1995	1	0	3	190.000
...	...	...	...	...	...	...	...	...	...

2.3. Normalización o escalado de datos (feature scaling)¶

Volvamos a la fórmula que hemos visto antes para estimar el precio de una vivienda, dados los parámetros de entrada:

Precio = a₁·Localidad + a₂·Superficie + a₃·Habitaciones + ...

Si observamos la tabla de datos, hay campos con valores bajos (Alicante, Piscina, Habitaciones) y otros con valores altos (Año, Superficie). Esto va a provocar que, en el cálculo final del precio, el valor de la superficie o el año de construcción sea mucho más determinante que si tiene piscina, o si está en Alicante. Para que todas las columnas que intervienen sean igual de relevantes en el cálculo del precio necesitamos homogeneizar los valores, y que todos estén dentro de un rango similar. Este proceso se llama escalado o normalización de los datos (feature scaling).

Hay que notar que es un proceso que debe hacerse justo antes de hacer la operación concreta que necesitamos (la estimación del precio) ya que, para otras cosas, no necesitamos alterar los valores originales de los datos.

Existen dos estrategias principales para escalar los datos:

Escalado por normalización: también llamada escalado min-max, deja todos los valores del conjunto en el rango de 0 a 1, aplicando la siguiente fórmula a cada valor:

\[ Val\;Normalizado = \frac{Val\;Actual - Min}{Max - Min} \]

Escalado por estandarización: consiste en calcular la media y desviación típica del conjunto de datos a tratar. En este caso, el rango de valores ya no va de 0 a 1, y admite valores negativos, pero al menos está acotado a un rango más controlado. El valor normalizado se calcula entonces como:

\[ Val\;Normalizado = \frac{Val\;Actual - Media}{\sigma} \]

Aplicando cualquiera de estas dos técnicas sobre las columnas de nuestra tabla, podemos tenerlas todas acotadas en el mismo rango de valores. Por ejemplo:

Alicante	Elche	San Vicente	Superficie	Habitaciones	Año	Ascensor	Piscina	Estado	Precio
1	0	0	0.8331	0.7500	0.8991	1	0	0.6667	180.000
0	1	0	1.0000	1.0000	1.0000	0	1	1.0000	260.000
1	0	0	0.5653	0.7500	0.5632	1	0	0.3333	165.000
0	0	1	0.8781	1.0000	0.5831	0	0	0.6667	170.000
0	0	1	0.4326	0.5000	0.5831	1	0	0.6667	190.000
...	...	...	...	...	...	...	...	...	...

Nota

La columna objetivo (el precio en nuestro caso) también se puede normalizar siguiendo el mismo procedimiento. Como paso final, existe un proceso de "desnormalización" donde podemos aplicar el cálculo inverso a un valor para saber cuál era su valor original, y así sacar el valor "desnormalizado".

Nota

Los valores one hot pueden escalarse o no, hay razones buenas en ambos casos, pero hay que tener en cuenta que, si los escalamos, perderemos esa noción de "pertenencia a una categoría" que nos dan los ceros y unos de cada columna, ya que pasarán a tener otros valores. Es habitual, por tanto, no escalarlos en muchos problemas.

3. Exploratory Data Analysis (EDA)¶

El análisis exploratorio de datos es una etapa que, como hemos comentado al inicio de este documento, puede realizarse antes, después o durante las etapas anteriores de limpieza e ingeniería. En esta etapa se examinan y visualizan los datos de distintos modos, para comprenderlos mejor, detectar algún tipo de correlación o patrones, y extraer información valiosa.

3.1. Variables estadísticas relevantes¶

Normalmente cuando trabajamos con un conjunto determinado de datos existen ciertas variables estadísticas que podemos extraer para hacernos una idea de los valores con los que vamos a trabajar:

Media
Desviación típica (promedio de diferencias entre los valores de un conjunto de datos, o cuánto se aleja en promedio cada valor de la media del conjunto)
Moda o valor más repetido
Valor máximo
Valor mínimo
Número de valores nulos
...

Muchas librerías en Python o R, por ejemplo, disponen de funciones útiles que, con una sola línea de código, nos extraen y muestran toda esta información.

3.2. Representaciones gráficas más relevantes¶

En cuanto a las representaciones gráficas que podemos obtener de las distintas columnas de un conjunto de datos, vamos a comentar a continuación algunas de las más habituales.

Mapas de correlación

Este componente ya lo hemos visto antes para analizar la selección de características. Es un diagrama que visualmente representa, en una tabla bidimensional con colores, las correlaciones existentes entre cada pareja de campos o columnas de un conjunto de datos. Valores cercanos a 1 indican una alta correlación directa, valores cercanos a -1 una alta correlación inversa, y valores cercanos a 0 indican que no hay correlación entre esos datos.

Histogramas

Son gráficos de barras que representan la frecuencia de los diferentes valores de un conjunto de datos. Por ejemplo, podríamos obtener cuántos inmuebles se han construido por cada año en nuestra tabla de inmuebles

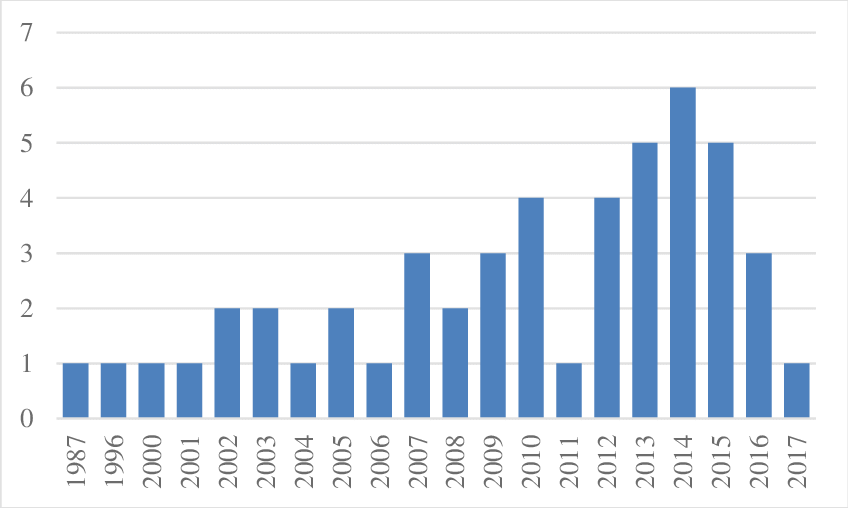
Gráficos de barras

Representan, vertical u horizontalmente, una correspondencia entre dos campos de una tabla. Por ejemplo, el precio medio de las viviendas por localidad

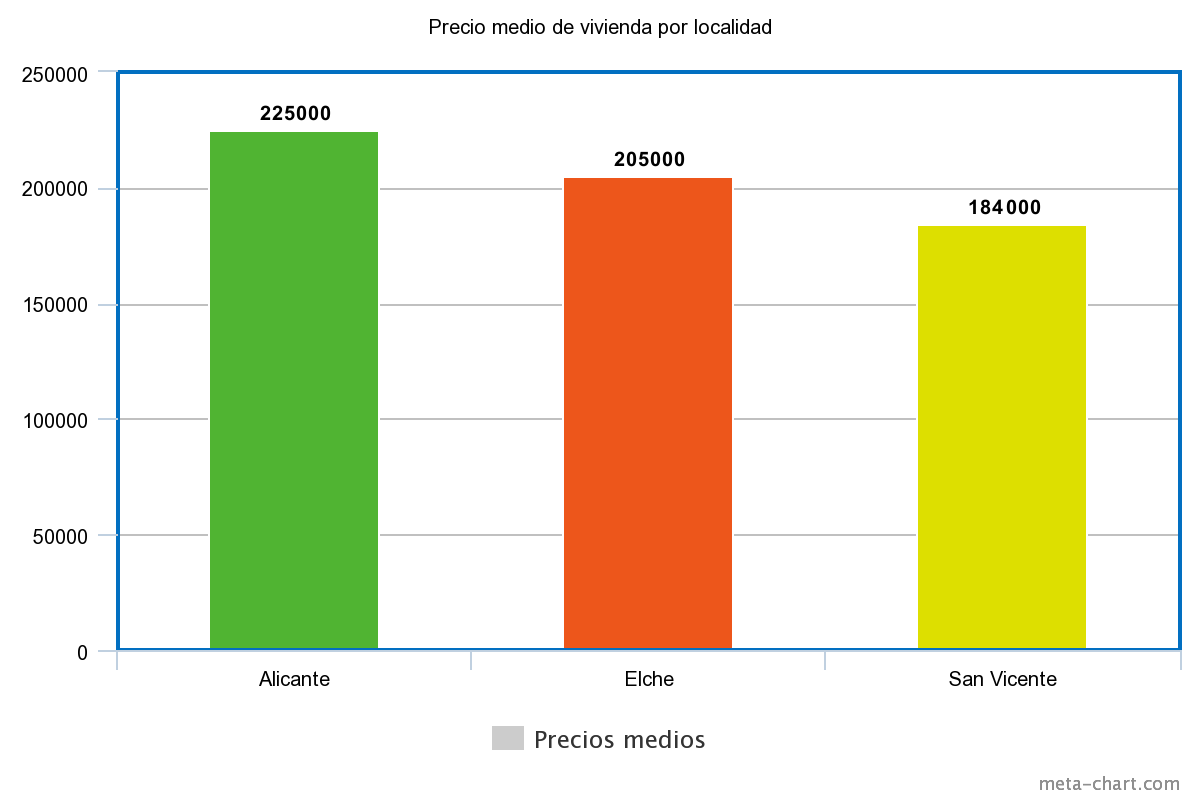
Gráficos circulares

Representan la proporción de unos datos frente a otros en un conjunto. Por ejemplo, el porcentaje de viviendas para cada localidad de la tabla

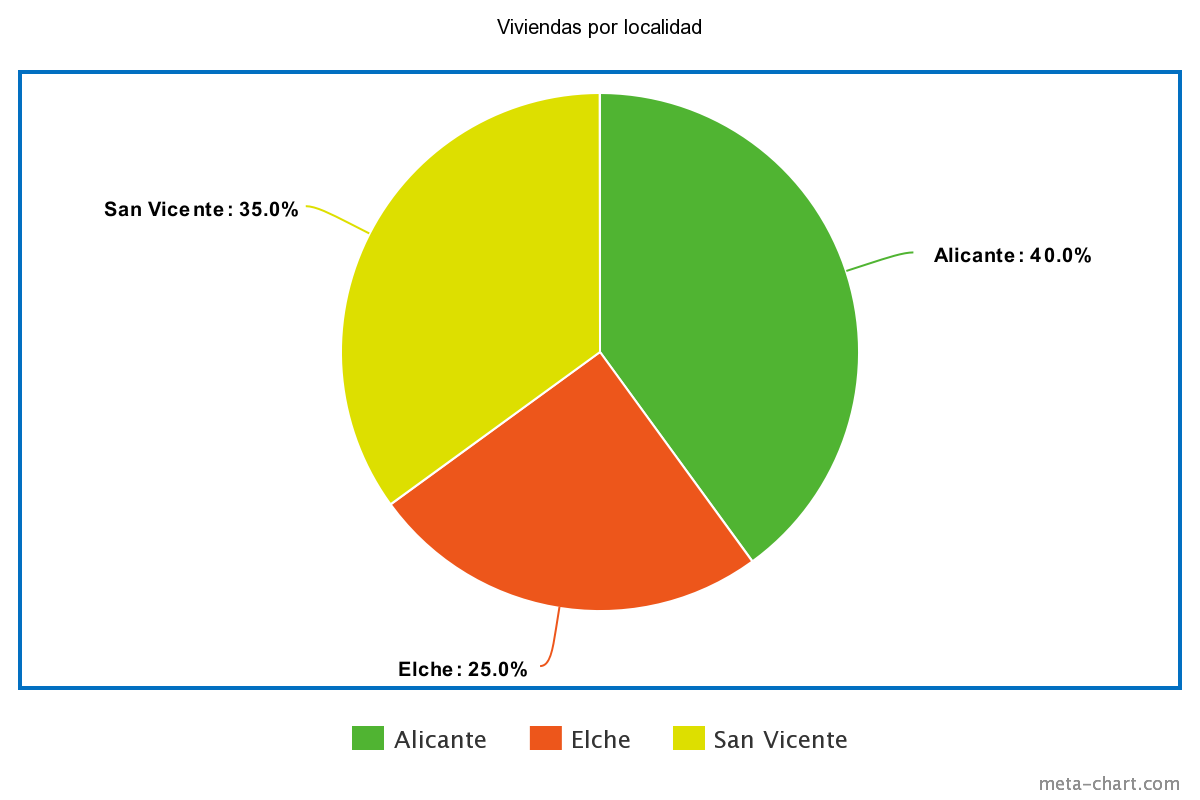
Gráficos de líneas

Son similares a los gráficos de barras, pero muestran de forma más continua la evolución de un valor. Por ejemplo, la evolución del precio medio de la vivienda según el año de construcción.

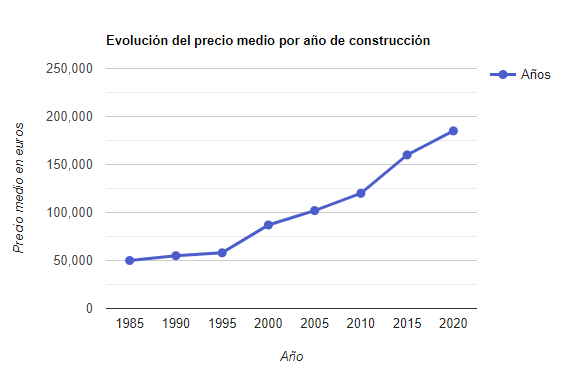
Gráficos de dispersión (scatter plots)

Muestran la correspondencia entre dos campos de un conjunto. Uno se dispone en el eje horizontal y otro en el vertical. Si se puede trazar una línea recta que más o menos pase cerca de los puntos, es que existe una alta correlación. Por ejemplo, podríamos establecer una correspondencia entre la superficie de la vivienda y el precio de venta.

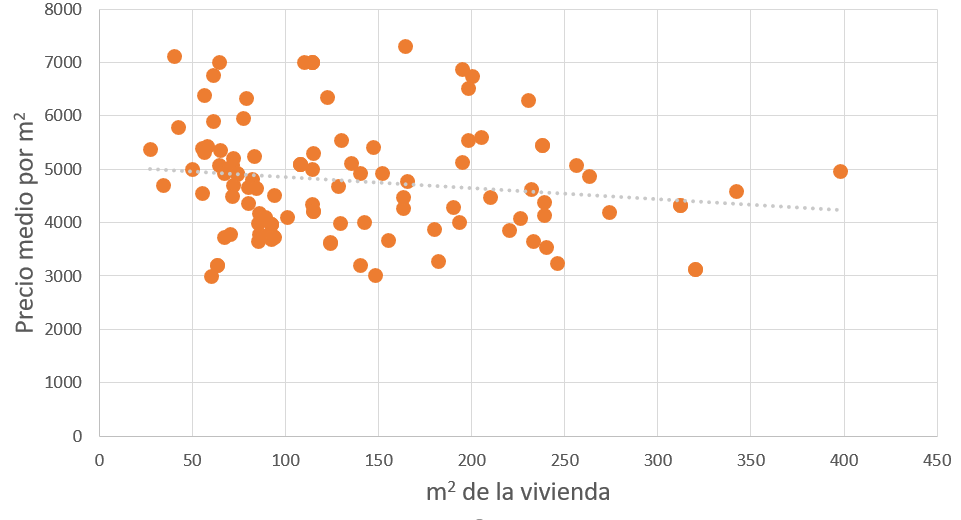
Gráficos de cajas (box plots)

Representan la dispersión de los datos agrupada por categorías. En cada categoría se muestra una caja con los cuartiles, siendo los "bigotes" inferior y superior los valores que se "salen" de los centrales. Las posibles anomalías (outliers) que pudiera haber se representan con puntos por encima o por debajo de los bigotes. Por ejemplo, podríamos representar los precios de las viviendas según su estado, y ver si hay viviendas que se salen de lo normal para el estado en el que están.

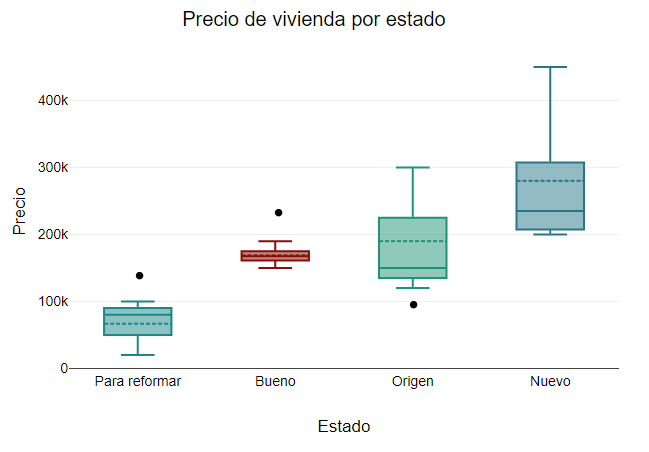
4. Librerías y recursos para análisis de datos¶

Existen multitud de librerías en los diferentes lenguajes empleados en data science que nos ayudan en todo este proceso de data cleaning, feature engineering y EDA. En Python, por ejemplo, podemos emplear las siguientes:

NumPy: una librería matemática para tratar listas de datos como arrays numéricos, lo que permite una manipulación más eficiente y precisa de esos datos.
Pandas: librería para análisis de datos, permite cargar datos de una fuente, filtrar las filas y columnas que nos interesen, realizar algunas transformaciones (limpieza, cálculos, etc)...
Matplotlib y Seaborn son dos ejemplos de librerías empleadas en la etapa de EDA para obtener distintas representaciones gráficas de lo datos

En el caso del lenguaje R disponemos de otras librerías similares, como son:

dplyr: librería similar a pandas en Python, para análisis y transformación de conjuntos de datos
ggplot2: librería para obtener representaciones gráficas de los datos.
Existen otras librerías de apoyo a las anteriores. Muchas de ellas se engloban dentro de un paquete general llamado tidyverse, que puede consultarse en su web oficial. De hecho, las dos librerías comentadas anteriormente forman parte de este ecosistema.

4.1. Fuentes de datos¶

Podemos descargar datasets o conjuntos de datos reales de diferentes lugares en Internet. Aquí indicamos algunos de ellos: